|
Introduction to
|
Course Syllabus
DISTRIBUTION OF MATERIALS
The slides and source codes are open to individuals with Columbia University email address. If you are interested at learning the materials, please submit a request via the Google drive, preferable with a brief statement explaining the reasons for your interest to the materials (e.g. for educational purpose). The specific term of usage of the materials in this website can be found [here].
CLASS SESSIONS
Guest Lecture: Tuesday and Thursday, 11:30am to 1:20pm at Shriram 104
TEXTBOOK
Supplement materials will be available online.
COURSE DESCRIPTION
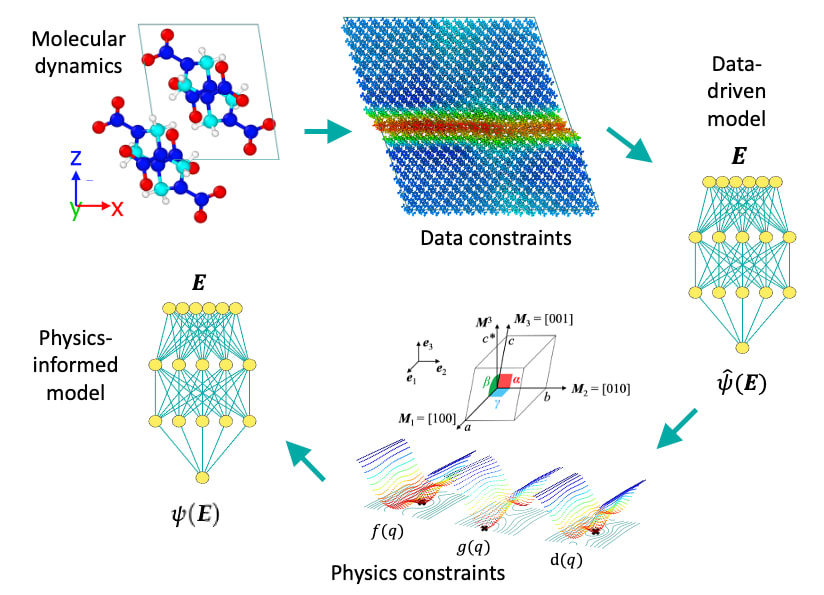
This course focuses on a geometric learning approach to derive, test, and validate a wide range of artificial intelligence enabled models for engineering (meta-materials, composites, alloys) and natural materials (soil, rock, clay). Students will learn how to incorporate a wide range of data stored in graphs, manifold and point sets to train neural networks to design optimal experiments, embed high-dimensional data, enforce mechanics and physical principles, de-noise data with geometry, and enable model-free simulations and discover causality of mechanisms that leads to the failures of materials.
PREREQUISITES
Linear algebra and mechanics of materials.
ASSESSMENT AND GRADING POLICY
Grades will be based on:
Lab Report 1 ............................................................ 10%
Lab Report 2 ............................................................ 10%
Lab Report 3 ............................................................10%
Lab Report 4 ............................................................ 10%
Quiz 1 .........................................................................10%
Quiz 2 .........................................................................10%
Comprehensive Final Project.................................... 40%
COURSE LOGISTICS
The course will be split into two parts. We will first cover the practical aspect of using neural network to generate models. We will assume that all the data are in the Euclidean space and apply constraints to generate the inductive bias necessary to complete the models. In the second part of the course, we will explore and experiments with different methods to generate constitutive models that are of sufficient robustness and accuracy for engineering practice. For each session, there will be a 1-to-1.5-hours of lecture followed by a COLAB tutorial.
The slides and source codes are open to individuals with Columbia University email address. If you are interested at learning the materials, please submit a request via the Google drive, preferable with a brief statement explaining the reasons for your interest to the materials (e.g. for educational purpose). The specific term of usage of the materials in this website can be found [here].
CLASS SESSIONS
Guest Lecture: Tuesday and Thursday, 11:30am to 1:20pm at Shriram 104
TEXTBOOK
Supplement materials will be available online.
COURSE DESCRIPTION
This course focuses on a geometric learning approach to derive, test, and validate a wide range of artificial intelligence enabled models for engineering (meta-materials, composites, alloys) and natural materials (soil, rock, clay). Students will learn how to incorporate a wide range of data stored in graphs, manifold and point sets to train neural networks to design optimal experiments, embed high-dimensional data, enforce mechanics and physical principles, de-noise data with geometry, and enable model-free simulations and discover causality of mechanisms that leads to the failures of materials.
PREREQUISITES
Linear algebra and mechanics of materials.
ASSESSMENT AND GRADING POLICY
Grades will be based on:
Lab Report 1 ............................................................ 10%
Lab Report 2 ............................................................ 10%
Lab Report 3 ............................................................10%
Lab Report 4 ............................................................ 10%
Quiz 1 .........................................................................10%
Quiz 2 .........................................................................10%
Comprehensive Final Project.................................... 40%
COURSE LOGISTICS
The course will be split into two parts. We will first cover the practical aspect of using neural network to generate models. We will assume that all the data are in the Euclidean space and apply constraints to generate the inductive bias necessary to complete the models. In the second part of the course, we will explore and experiments with different methods to generate constitutive models that are of sufficient robustness and accuracy for engineering practice. For each session, there will be a 1-to-1.5-hours of lecture followed by a COLAB tutorial.
Online Course Materials
Date |
Topic |
Lecture |
External Reading |
Assignment |
Tutorial |
1/10 |
Course overview, logistic and miscellaneous items |
[Slide] |
N/A |
N/A |
|
1/12 |
Computer Lab: Supervised learning with labeled data: nonlinear regression via neural nets, non-convex optimization, hyper-parameter tuning |
[Colab] |
Google Deepmind X ICL course: [URL] |
Lab Task 1 given |
Value |
1/17 |
Supervised learning for elastic energy functional |
[Slide] |
N/A |
MMLDT tutorial: [Video] |
|
1/19 |
Building the learning algorithm with group data: regularization, physics constraints, symmetry, Lie group/Algebra |
[Video] |
N/A |
|
|
1/24 |
Recurrent neural network for plasticity: Numerical experiments with Long short-term memory, gated recurrent neural network, and attention-based transformer. |
[Slide] |
Lab Report 1 due; Lab Task 2 given |
Colab for traction-separation law: [Colab] |
|
1/26 |
Neural network yield surface and level sets: Theory |
[Slide] |
N/A |
||
1/31 |
Neural network yield surface and level sets: Implementation |
N/A |
|||
2/2 |
Physics-informed neural network as a partial differential equation solver |
[Slide] |
Lab Report 2 due Lab Task 3 given |
||
2/7 |
Overview on non-Euclidean machine learning: metrics, de-noising and optimal transport |
Value |
Value |
Value |
|
2/9 |
Geometric Learning Part I: Graph learning in mechanics before machine learning |
N/A |
Embedding of finite element solution [Colab] |
||
2/14 |
Geometric Learning Part I: Graph embedding for nonlinear elasticity (node embedding) |
[Slide] |
Semi-supervised learning for a surrogate family [URL] |
Lab Report 3 due |
|
2/16 |
Geometric Learning Part I: Graph embedding and autoencoders for plasticity (graph pooling) |
Graph embedding for plastic deformation: [URL] |
N/A |
||
2/21 |
Geometric Learning Part I: Directed graph, tree, decision tree, and Monte Carlo Tree search for long-term planning |
Value |
Lab Task 4 given |
||
2/23 |
Guest Lecture 1: deep reinforcement learning for the design of experiments Guest Lecture 2: Causal discovery for mechanics |
Value |
N/A |
Value |
|
2/28 |
Geometric Learning Part II: Manifold |
[Slide] |
Lab Report 4 due |
||
3/2 |
Geometric Learning Part II: Model-free elasticity |
Value |
Value |
||
3/7 |
Geometric Learning Part II: Manifold embedding for de-noising |
Value |
N/A |
||
3/9 |
Final project presentations |
N/A |
N/A |
|
|
|
Copyright @ 2014-2024. All rights reserved.