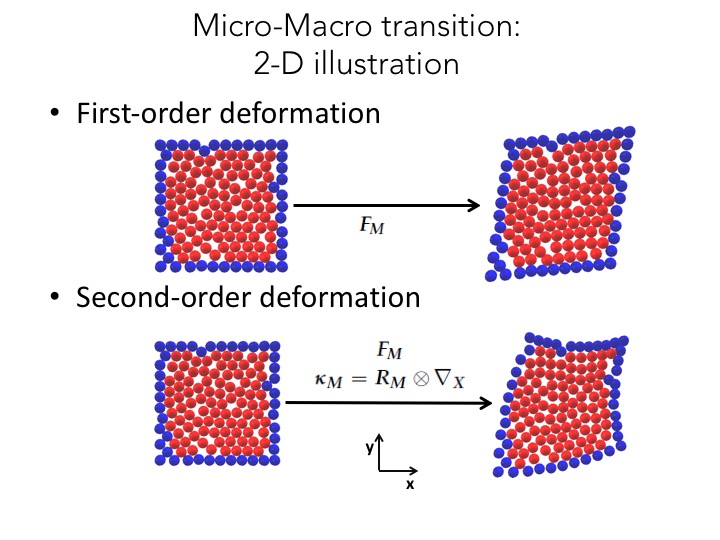
Research Theme
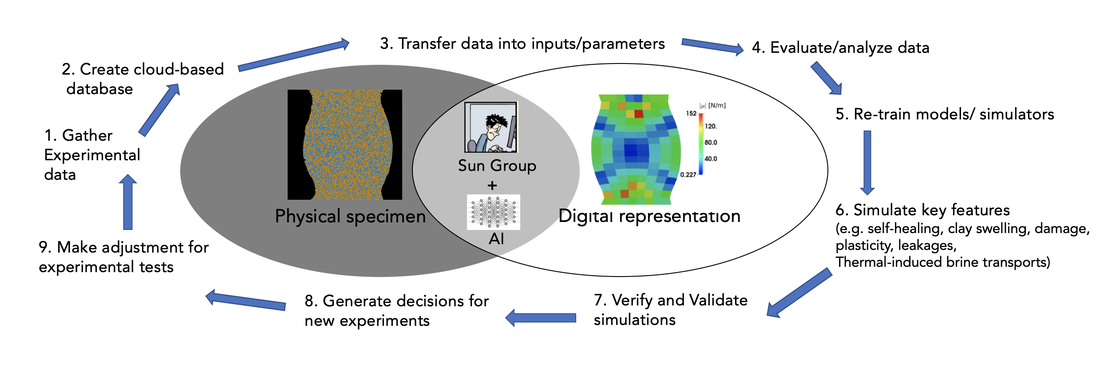
The objective of our group's research is to develop theoretical and numerical models that aid more accurate predictions for engineering design and applications. We act as a bridge among mathematical principles, data science and engineering industry. As a result, we emphasize on both the mathematical foundations and the practicality when deriving models for specific engineering problems. The figure below summarizes some of the current and previous work of this research group. Examples of previous and ongoing research conducted by the research group are listed below.
Geometrical symbolic regression for interpretable constitutive modeling
Conventionally, symbolic regression is often limited to function with one or two variables (see the benchmark). For mechanics models, especially the one that requires a large number variables to describe complex phenomena, symbolic regression is often out of reach as a tool.
Meanwhile, conventional neural network is highly expressive but lacks the interpretability of a concise analytical expression. In the case where the neural network used to express the function is large, the calculation via neural network also takes up more memory and computational time and hence not suitable for large-scale solid mechanics simulations.
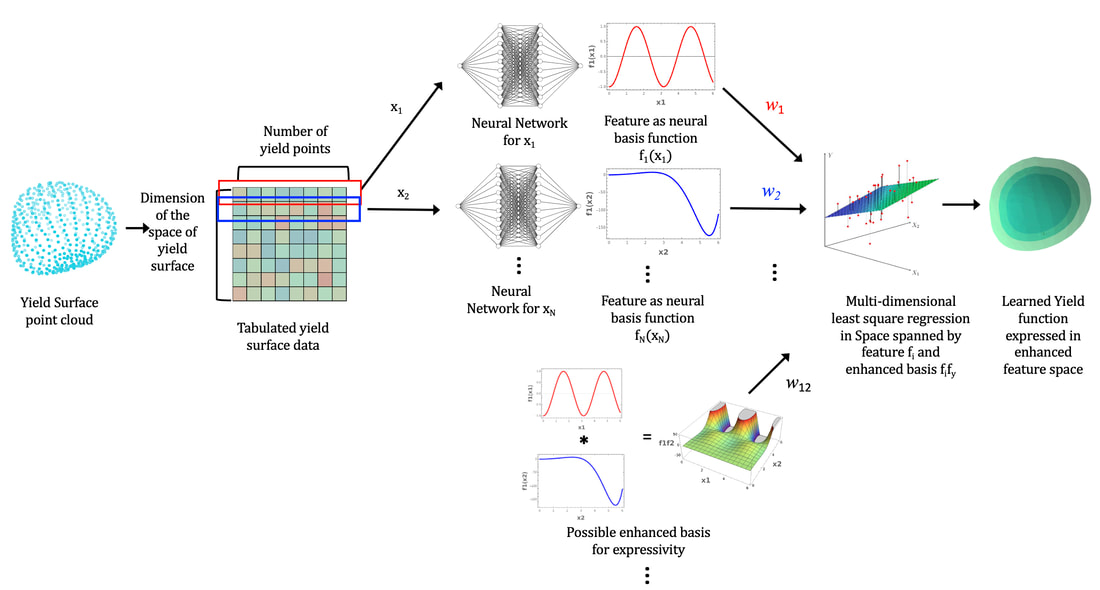
In this line of research, we introduce a two-step machine-learning approach that returns mathematical models interpretable by human experts.
In particular, we hypothesize that a mathematical model (e.g., yield surfaces or hyperelastic energy functionals) can be expressed in terms of a set of single-variable feature mappings obtained from supervised learning. This idea of feature space can be linear (also see the Neural Additive Model) but may also be extended to polynomials (see Figure below).
Meanwhile, conventional neural network is highly expressive but lacks the interpretability of a concise analytical expression. In the case where the neural network used to express the function is large, the calculation via neural network also takes up more memory and computational time and hence not suitable for large-scale solid mechanics simulations.
In this line of research, we introduce a two-step machine-learning approach that returns mathematical models interpretable by human experts.
In particular, we hypothesize that a mathematical model (e.g., yield surfaces or hyperelastic energy functionals) can be expressed in terms of a set of single-variable feature mappings obtained from supervised learning. This idea of feature space can be linear (also see the Neural Additive Model) but may also be extended to polynomials (see Figure below).
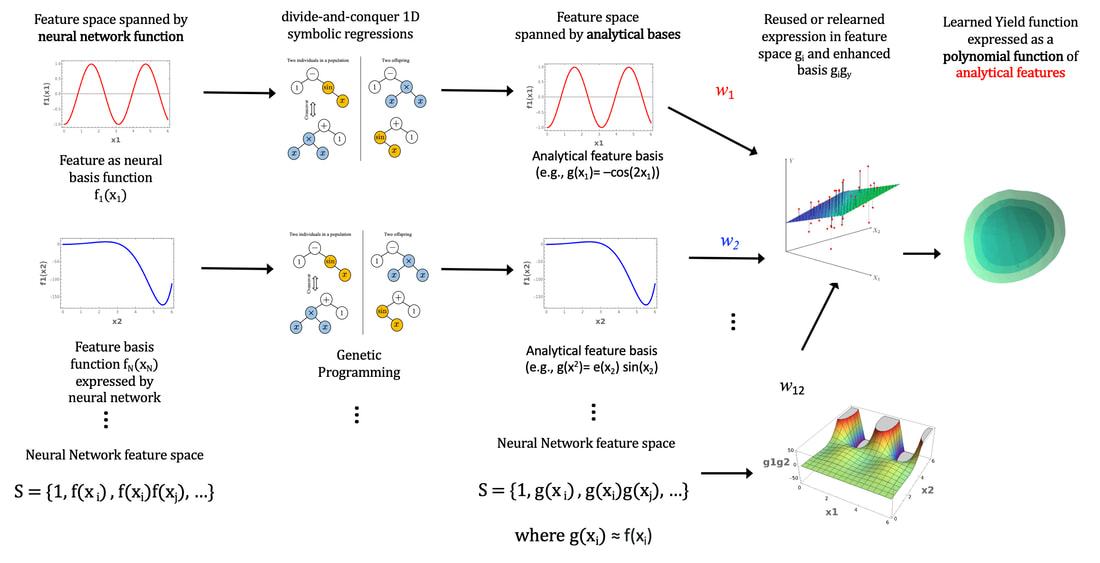
A post-processing step is then used to re-interpret the set of single-variable neural network mapping functions into mathematical form through symbolic regression (see below). This divide-and-conquer approach provides several important advantages. First, it enables us to overcome the scaling issue of symbolic regression algorithms. From a practical perspective, it enhances the portability of learned models for partial differential equation solvers written in different programming languages.
Related publications:
- B. Bahmani, W.C. Sun, Discovering interpretable elastoplasticity models via the neural polynomial method enabled symbolic regressions, under review. (Arxiv first submitted on 24th July 2023.) [Arxiv]
B. Bahmani, W.C. Sun, Physics-constrained symbolic model discovery for polyconvex incompressible hyperelastic materials, under review. (Arxiv first submitted on 6th Oct, 2023.) [Arxiv]
- Bahador Bahmani, 01/2023 - current
- Huijian Cai, 09/2023 - current
- Nhon Phan, 10/2023 - current
Geometric Learning for computational solid mechanics (with manifold data)
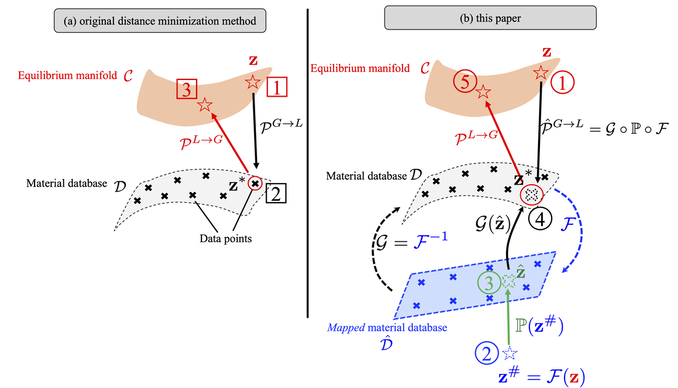
Distance-minimization model-free data approach introduced by Kirchdoerfer & Ortiz provides a completely new paradigm to run physical simulations of deformable without constitutive laws.
Yet, key technical barriers include the high demand on the data in the phase space, the combinatorial search of the discrete data set and the arbitrary notion of norms equipped for the phase space. In this work, we introduce a deep neural network to globally map data from the constitutive manifold onto a lower-dimensional Euclidean vector space. As such, we establish the relation between the norm of the mapped Euclidean vector space and the metric of the manifold and lead to a more physically consistent notion of distance for the material data. This treatment in return allows us to bypass the expensive combinatorial optimization, which may significantly speed up the model-free simulations when data are abundant and of high dimensions. Meanwhile, the learning of embedding also improves the robustness of the algorithm when the data is sparse or distributed unevenly in the parametric space.
Another idea we have attempted earlier, which is now published in CMAME, is to create a hybridized model-based/model-free approach to handle multi-physics problems where data of different constitutive responses are often of different fidelities or if one of the data set does not provide sufficient data for model-free approach (i.e. Darcy's flow vs. stress-strain relation). Furthermore, to deal with the costly combinatorial search, we have adopted a KD tree search to speed up the local search.
Related publications:
Yet, key technical barriers include the high demand on the data in the phase space, the combinatorial search of the discrete data set and the arbitrary notion of norms equipped for the phase space. In this work, we introduce a deep neural network to globally map data from the constitutive manifold onto a lower-dimensional Euclidean vector space. As such, we establish the relation between the norm of the mapped Euclidean vector space and the metric of the manifold and lead to a more physically consistent notion of distance for the material data. This treatment in return allows us to bypass the expensive combinatorial optimization, which may significantly speed up the model-free simulations when data are abundant and of high dimensions. Meanwhile, the learning of embedding also improves the robustness of the algorithm when the data is sparse or distributed unevenly in the parametric space.
Another idea we have attempted earlier, which is now published in CMAME, is to create a hybridized model-based/model-free approach to handle multi-physics problems where data of different constitutive responses are often of different fidelities or if one of the data set does not provide sufficient data for model-free approach (i.e. Darcy's flow vs. stress-strain relation). Furthermore, to deal with the costly combinatorial search, we have adopted a KD tree search to speed up the local search.
Related publications:
- B. Bahmani, W.C. Sun, Manifold embedding data-driven mechanics, Journal of Mechanics and Physics in Solids, accepted, 2022. [Video][Preprint]
- B. Bahmani, W.C. Sun, A kd-tree accelerated hybrid data-driven/model-based approach for poroelasticity problems with multi-fidelity multi-physics data, Computer Methods in Applied Mechanics and Engineering, doi:10.1016/j.cma.2021.113868, 2021. [Video] [PDF]
- B. Bahmani, W.C. Sun, Distance-preserving manifold de-noising for data-driven mechanics, Computer Methods in Applied Mechanics and Engineering, doi:10.1016/j.cma.2022.115857, 2022. [URL]
- Bahador Bahmani, 09/2019 - current
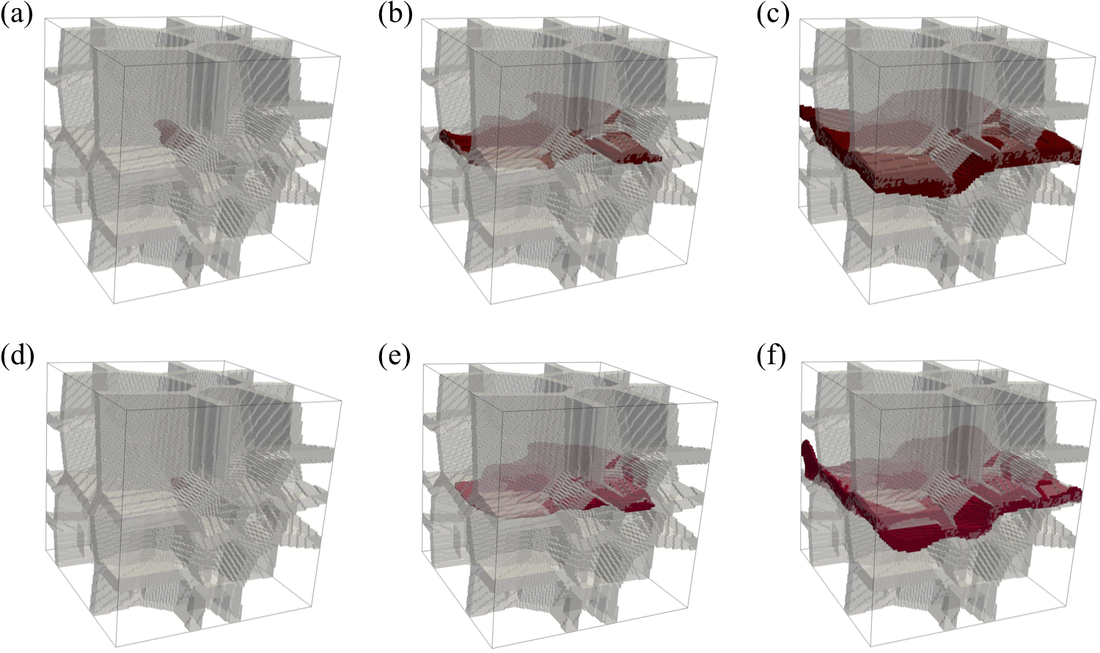
Geometric Learning for computational solid mechanics (with graph data)
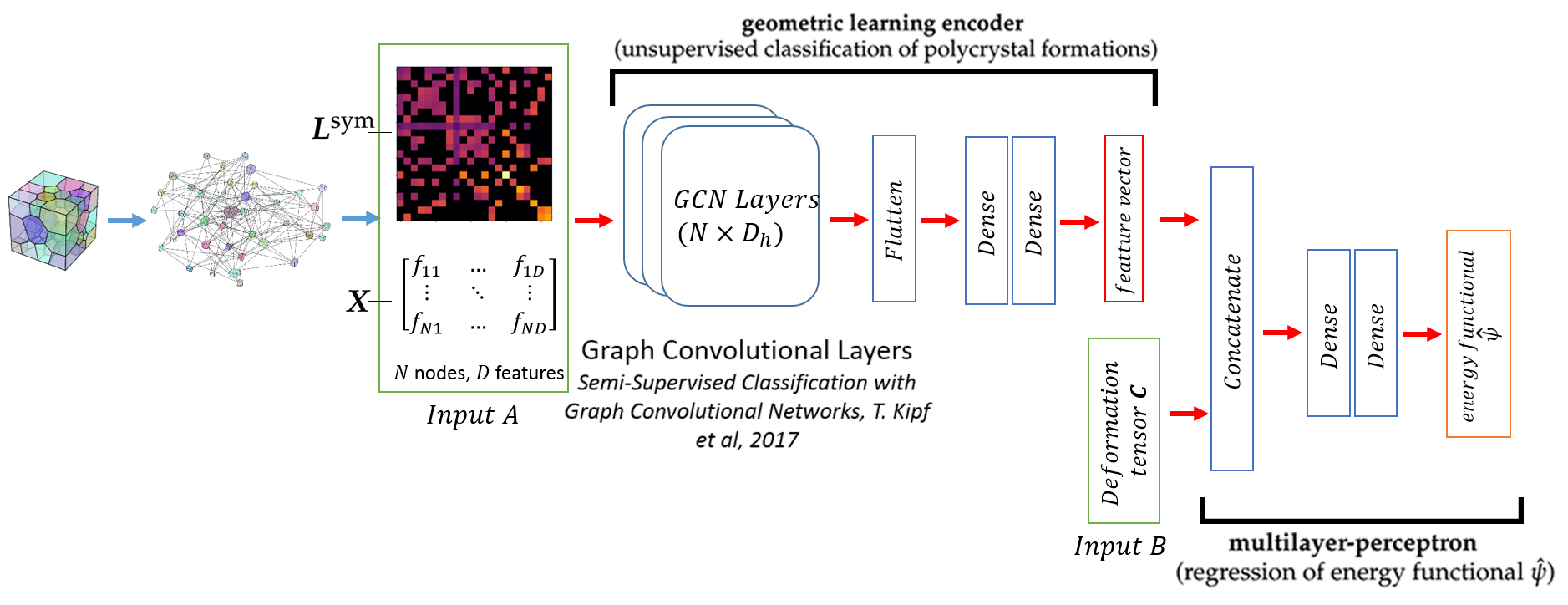
In this work, our goal is to incorporate non-Euclidean microstructural data and create interpretable descriptors to create a graph-based elasto-plasticity model. While traditional hyperelasticity models often incorporate homogenized measures of microstructural attributes, such as porosity, averaged orientation of constitutes, these measures cannot reflect the topological structures of the attributes. We fill this knowledge gap by introducing the concept of a weighted graph as a new means to store topological information, such as the connectivity of anisotropic grains in assembles. Then, by leveraging a graph convolutional deep neural network architecture in the spectral domain, we introduce a mechanism to incorporate these non-Euclidean weighted graph data directly as input for training and for predicting the elastic responses of materials with complex microstructures. To ensure smoothness and prevent non-convexity of the trained stored energy functional, we introduce a Sobolev training technique for neural networks such that stress measure is obtained implicitly from taking directional derivatives of the trained energy functional. By optimizing the neural network to approximate both the energy functional output and the stress measure, we introduce a training procedure the improves efficiency and generalize the learned energy functional for different microstructures.
Related publications:
Related publications:
- N. Vlassis, W.C. Sun, Sobolev training of thermodynamic-informed neural network for interpretable elasto-plasticity models with level set hardening, Computer Methods in Applied Mechanics and Engineering, doi:10.1016/j.cma.2021.113695, 2021. [Video][preprint]
- Y. Heider", H.S. Suh, W.C. Sun, An offline multi-scale unsaturated poromechanics model enabled by self-designed/self-improved neural network, International Journal for Numerical and Analytical Methods in Geomechanics, doi:10.1002/nag.3196, 2021.
- N. Vlassis, R. Ma", W.C. Sun, Geometric deep learning for computational mechanics Part I: Anisotropic Hyperelasticity, Computer Methods in Applied Mechanics and Engineering, 2020. [arxiv]
- C. Cai, N. Vlassis, L. Magee, R. Ma", Z. Xiong, B. Bahmani, T-F Wong, Y. Wang, W.C. Sun, Equivariant geometric learning for digital rock physics. Part I: Estimating formation factor and effective permeability tensors, International Journal for Multiscale Computation and Engineering, accepted, 2021.[arxiv]
- Nikolaos Vlassis, 09/2017 - current
- Ran Ma, 01/2019 - current
- Bahador Bahmani, 09/2019 - current
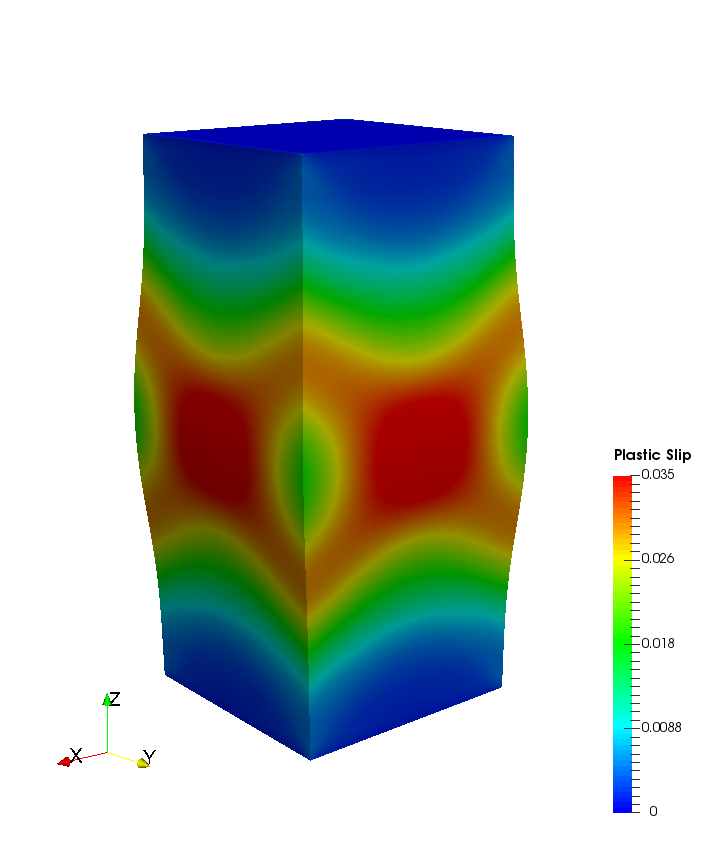
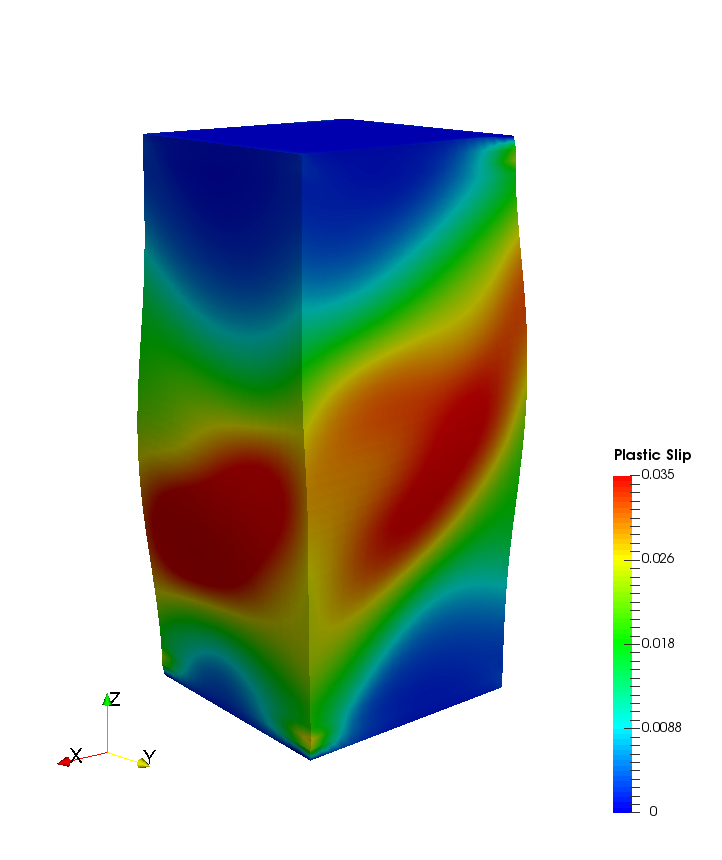
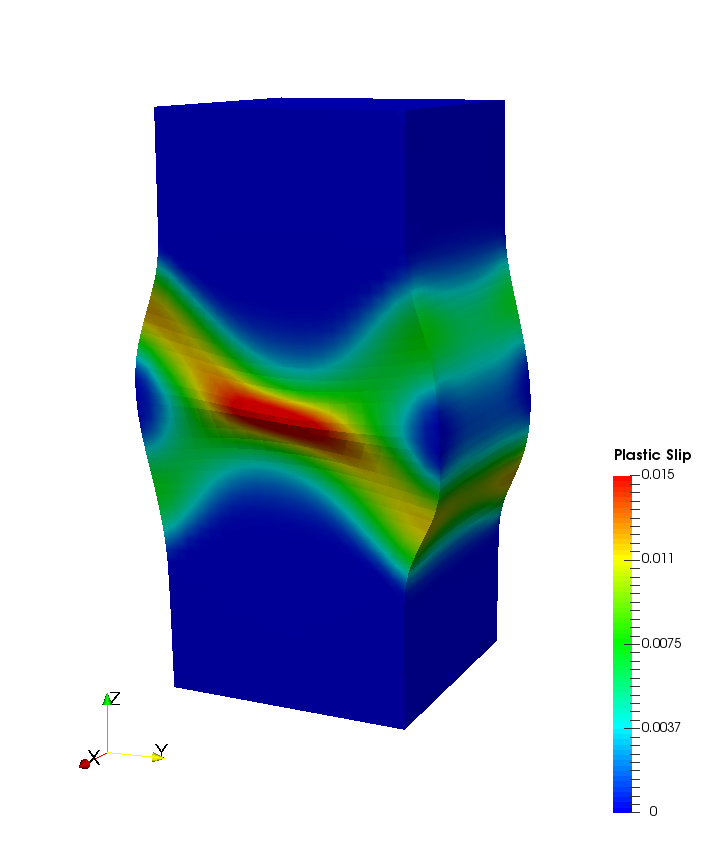
Sobolev training for interpretable machine learning plasticity model
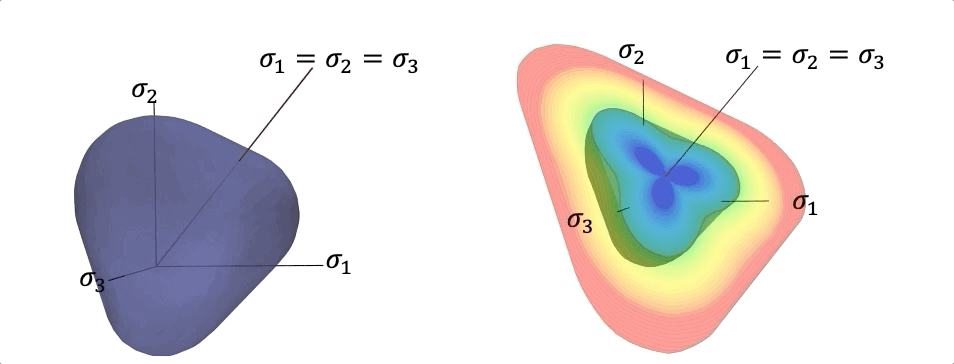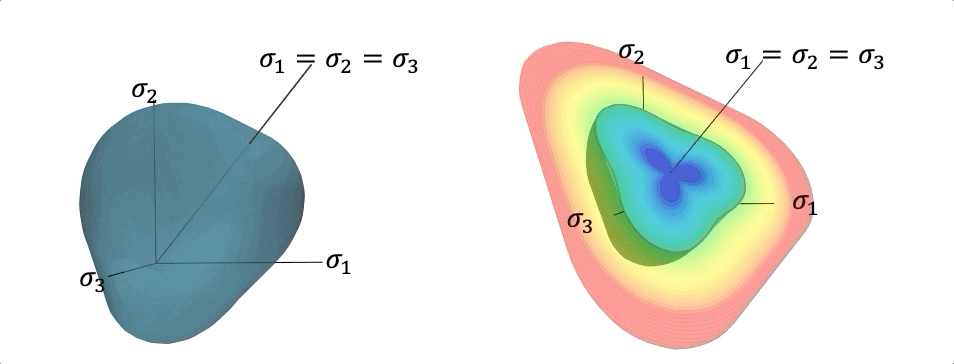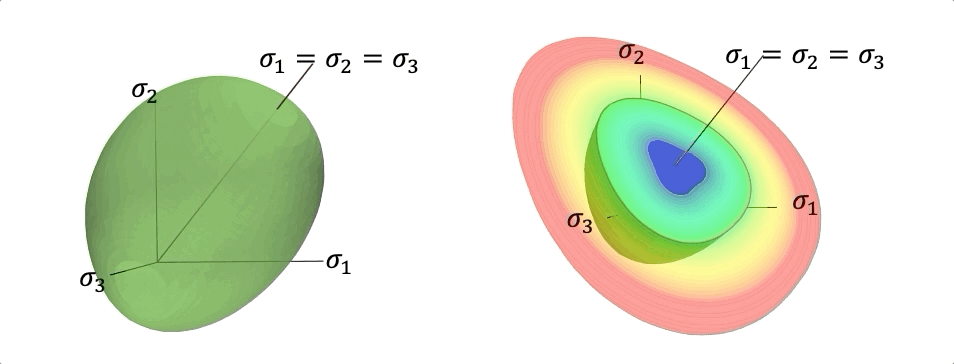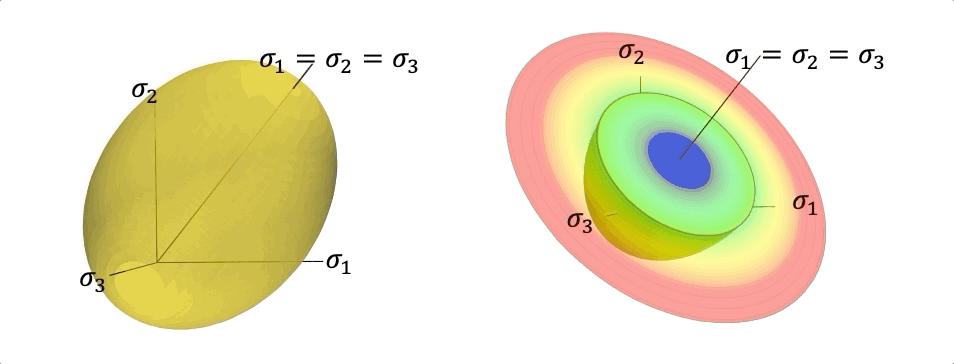Different plasticity models recovered from the machine learning driven level set yield function. Instead of hand-crafting yield function, flow rules, and hardening laws, these components are generated from data via Sobolev training
To circumvent the lack of interpretability of the classical black-box neural network, we introduce a higher-order supervised machine learning technique that generates components of elasto-plastic models such as elasticity functional, yield function, hardening mechanisms, and plastic flow. The geometrical interpretation in the principal stress space allows us to use convexity and smoothness to ensure thermodynamic consistency. The speed function from the Hamilton-Jacobi equation is deduced from the DNS data to formulate hardening and non-associative plastic flow rules governed by the evolution of the low-dimensional descriptors. By incorporating a non-cooperative game that determines the necessary data to calibrate material models, the machine learning generated model is continuously tested, calibrated, and improved as new data guided by the adversarial agents are generated. A graph convolutional neural network is used to deduce low-dimensional descriptors that encodes the evolutional of particle topology under path-dependent deformation and are used to replace internal variables. The resultant constitutive laws can be used in a finite element solver or incorporated as a loss function for the physical-informed neural network run physical simulations.
Related publications:
- N. Vlassis, W.C. Sun, Sobolev training of thermodynamic-informed neural network for interpretable elasto-plasticity models with level set hardening, Computer Methods in Applied Mechanics and Engineering, doi:10.1016/j.cma.2021.113695, 2021. [Video][preprint]
- N. Vlassis, W.C. Sun, Component-based machine learning paradigm for discovering rate-dependent and pressure-sensitive level-set plasticity models, Journal of Applied Mechanics, doi:10.1115/1.4052684, 2021.
- Nikolaos Vlassis, 09/2017 - current
- Mian Xiao, 09/2020 - current
- Bahador Bahmani 09/2019 - current
High-strain-rate responses of energetic materials
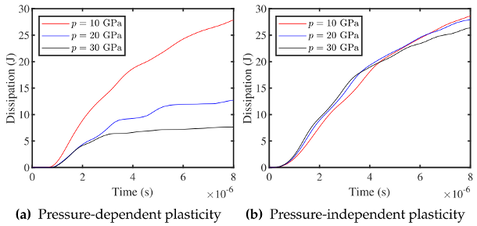
The thermomechanical response of the energetic material under impacting is closely related to its safety and reliability during processing, storage, and transportation. The goal of this project is to establish a multiscale and multiphysics model to predict the shock loading resistance of the energetic material. In our previous work, we developed a pressure-dependent anisotropic hyperelasticity and crystal plasticity model to incorporate pressure sensitivity while predicting the plastic dissipation. It is found that the external pressure has a strong influence on the plastic dissipation under shock loading, which cannot be captured by traditional crystal plasticity model. The material point method (MPM) is a hybrid Eulerian-Langrangian method, which is immune to mesh distortion and hence suitable for large deformation simulation. Also, MPM provides automatic no-penetration no-slip contact algorithm which enables the pore-collapse simulation. In our preliminary results with Johnson-Cook model, it is found that the heat-induced strain softening and shear band can be reproduced with MPM. We are currently working on introducing the anisotropic phase field fracture model into the MPM to simulate the fracture near the collapsing pores and related heat generation.
Related publications:
Related publications:
- R. Ma, W.C. Sun, C. R. Picu, Atomistic-model informed pressure-sensitive crystal plasticity for crystalline HMX, International Journal of Solid and Structures, 232:111170, doi:10.1016/j.ijsolstr.2021.111170, 2021.
- R. Ma, W.C. Sun, A finite micro-rotation material point method for micro-polar solid and fluid dynamics with three-dimensional evolving contacts and free surfaces, Computer Methods in Applied Mechanics and Engineering, doi:10.1016/j.cma.2021.114540, 2022.
- Ran Ma, 09/2019 - current
- Nick Vlassis, 09/2020-current
- Mian Xiao, 09/2021-current
Meta-modeling for computational mechanics: modeling the process of writing a material model
|
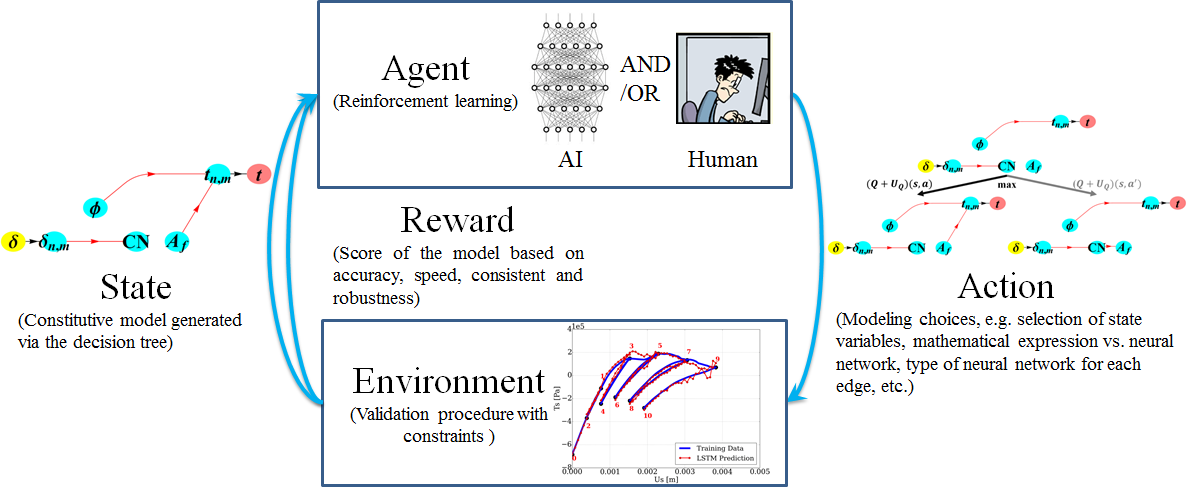
Our goal in this research is to not write material models for simulation but simulate how modelers write a model by interpreting data. In many machine learning applications for physics problems, the majority of time is spent on solving the optimization problems (tuning hyper-parameters, balancing constraints for boundary and governing laws). Here our objective is to take a more human approach where we also attempt to build an interpretable explanation abstracted by knowledge graphs.
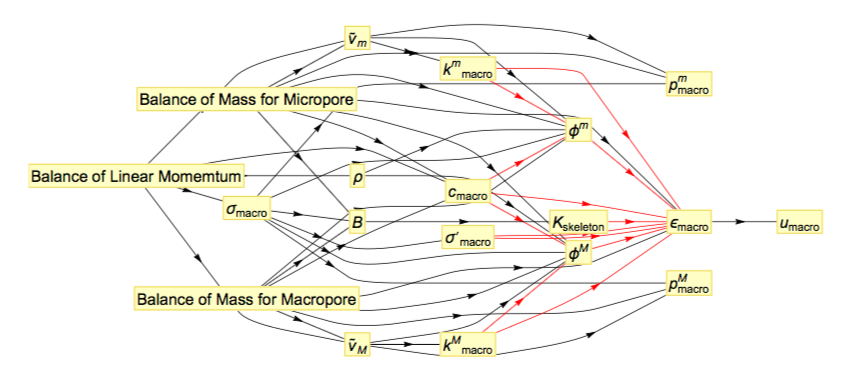
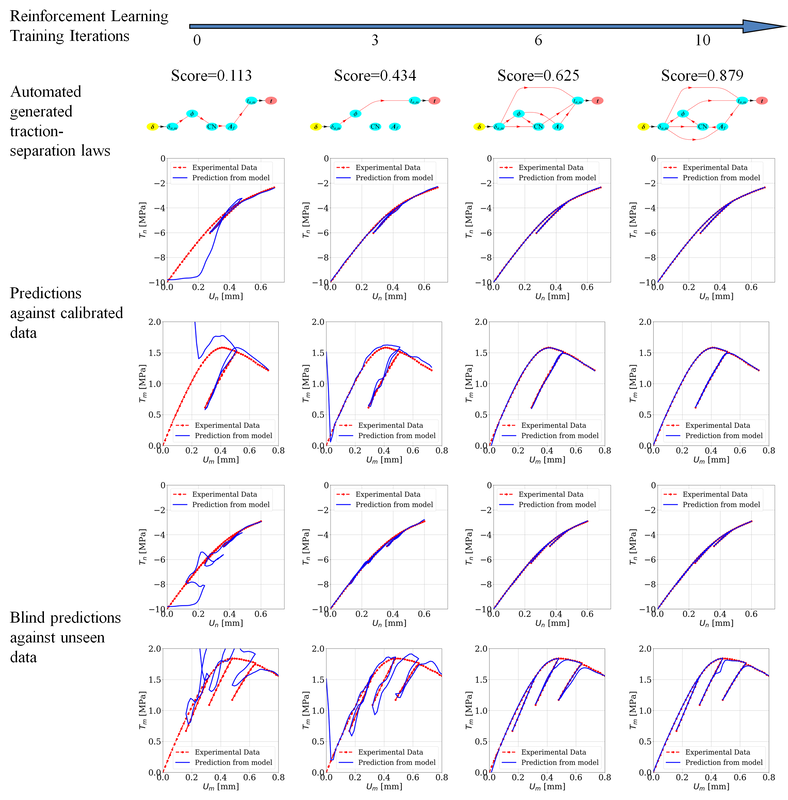
In this meta-modeling framework, all data accessible by the agents is modeled as labelled vertices (e.g. porosity, permeability) and all possible ways to connect those vertices are modeled as directed edges (e.g. mathematical expression, neural nets, support vector machine). Therefore, all the possible actions of the agents are mathematically represented by a labeled directed multi-graph. The learning process is therefore re-cast as the procedure to find a directed graph that links the input and output data with the optimal set of edges that maximize the reward (the objective function that measures the prediction qualities). With well-defined agents, reward, action space and environment, the AI modeler will then improve its ability to write the models through self-practicing in a deep reinforcement learning framework. Like humans, it will attempt to take different actions to write a model, then estimate the reward of each action via a deep neural network in a Monte Carlo tree search. By leveraging the ability of the AI modeler to repetitively practice and improve its modeling skills, we demonstrate that the proposed algorithm is able to both discover new hidden hierarchical structures of mechanics knowledge and rediscover well-known mechanics knowledge without any human intervention. In the case where availability of data is limited, the meta-modeling algorithm also explores the weakness of links in the constitutive laws and explores the optimal set of experiments to yield the best forward predictions under a limited budget. We use a dual-permeability problem as a test bed to demonstrate how this new modeling approach works. |
The meta-modeling model: a modeling effort to model the agent that writes constitutive laws.
Directed graph which represents a computational model. Red arrow represents relations that could be predicted by (1) multiscale simulations, (2) phenomenological laws, and (3) neural network models. A model selection procedure is used such that the optimal configuration is determined.
Self-improvement of the computer agent over each constitutive model writing session. Over time, the computer agent learns the directed graph that represents the relationships among physical quantities and employ this knowledge to write constitutive laws.
|
Team Members:
- Qing Yin 03/2021 - current
- Kun Wang, 09/2014 - 09/2018
- Nikolaos Vlassis, 09/2017 - current
- Xinran Zhong, 09/2016 - 08/2018
- Yousef Heider 10/2018-12/2020
- Jarett Poliner, 2020 - current
- K. Wang, W.C. Sun, A multiscale multi-permeability poroplasticity model linked by recursive homogenizations and deep learning, Computer Methods in Applied Mechanics and Engineering, accepted, 2018. [PDF]
- K. Wang, W.C. Sun, Meta-modeling game for deriving theoretical-consistent, micro-structural-based traction-separation laws via deep reinforcement learning, Computer Methods in Applied Mechanics and Engineering, doi:10.1016/j.cma.2018.11.026, 2019. [URL]
- K. Wang, W.C. Sun, An updated Lagrangian LBM-DEM-FEM coupling model for dual-permeability porous media with embedded discontinuities, Computer Methods in Applied Mechanics and Engineering, doi:10.1016/j.cma.2018.09.034, 2010.
- K. Wang, W.C. Sun, Q. Du, A cooperative game for automated learning of elasto-plasticity knowledge graphs and models with AI-guided experimentation, Computational Mechanics, special issue for Data-Driven Modeling and Simulations: Theory, Methods and Applications, 64(2):67–499, doi:,10.1007/s00466-019-01723-1, 2019. [PDF]
- Y. Heider", K. Wang, W.C. Sun, SO(3)-invariance of graph-based deep neural network for anisotropic elastoplastic materials, Computer Methods in Applied Mechanics and Engineering, 2020.
- A. Fuchs, Y. Heider", K. Wang, W.C. Sun, M. Kaliske, DNN2: A hyper-parameter reinforcement learning game for self-design neural network elasto-plastic constitutive laws, Computer and Structures, 249:106505, doi:10.1016/j.compstruc.2021.106505, 2021.
- X. Sun, B. Bahmani, N. Vlassis, W.C. Sun, Y. Xu, Data-driven discovery of interpretable causal relations for deep learning material laws with uncertainty propagation, Granular Matter, doi:10.1007/s10035-021-01137-y, 2021.
Modified material point method for complex geometries undergoing finite deformation
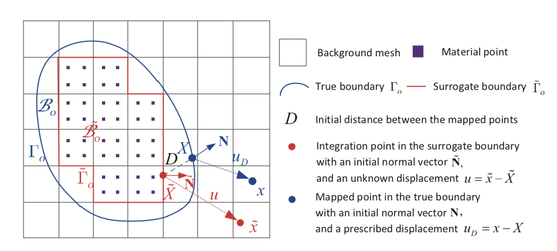Shifted domain technique applied on material point method.
One key drawback of classical discrete element methods for particulate mechanics is that they cannot generate any kinetic and kinematics information at the sub-grain scales. Nevertheless, many dissipative mechanisms of granular materials are actually originated from path-dependent behaviors at the sub-grain scales where wear, damage, fracture and fragmentation occurs. Nevertheless, recovery of these sub-scale information while capturing the geometry and form of each individual grains is inherently a difficult task.
The goal of this research is to establish an efficient image-to-simulation workflow to overcome this technical barrier. We introduce a mathematical framework designed to enable a simple image-to-simulation workflow for solids of complex geometries undergoing large deformation in the geometrically nonlinear regime. In particular, we adopt the integration scheme of the material point method to resolve the convergent issues for Lagrangian meshes due to mesh distortion, while using a shifted domain technique originated from Scovazzi and coworker to represent the boundary condition implicitly via a level set or signed distance function. Consequently, this method completely bypasses the need to generate high-quality conformal mesh to represent complex geometries and therefore allows modelers to select the space of the interpolation function without the constraints due to the geometrical need. This important simplification enables us to simulate deformation of complex geometries inferred from voxel images. Verification examples on deformable body subjected to finite rotation have shown that the new shifted domain material point method is able to generate frame-indifference results. Meanwhile, simulations using microCT images of a Hostun sand have demonstrated that this method is able to reproduce the quasi-brittle damage mechanisms of single grain without the excessively concentrated nodes commonly displayed in conformal meshes that represent 3D objects with local fine details.
Originally written/last updated 1/31/2019.
Team Members:
Published Work:
The goal of this research is to establish an efficient image-to-simulation workflow to overcome this technical barrier. We introduce a mathematical framework designed to enable a simple image-to-simulation workflow for solids of complex geometries undergoing large deformation in the geometrically nonlinear regime. In particular, we adopt the integration scheme of the material point method to resolve the convergent issues for Lagrangian meshes due to mesh distortion, while using a shifted domain technique originated from Scovazzi and coworker to represent the boundary condition implicitly via a level set or signed distance function. Consequently, this method completely bypasses the need to generate high-quality conformal mesh to represent complex geometries and therefore allows modelers to select the space of the interpolation function without the constraints due to the geometrical need. This important simplification enables us to simulate deformation of complex geometries inferred from voxel images. Verification examples on deformable body subjected to finite rotation have shown that the new shifted domain material point method is able to generate frame-indifference results. Meanwhile, simulations using microCT images of a Hostun sand have demonstrated that this method is able to reproduce the quasi-brittle damage mechanisms of single grain without the excessively concentrated nodes commonly displayed in conformal meshes that represent 3D objects with local fine details.
Originally written/last updated 1/31/2019.
Team Members:
- Mian Xiao, 09/2020-current
- Chuanqi Liu, 09/2018-09/2020
- Ran Ma, 01/2021-current
Published Work:
- C. Liu, W.C. Sun, Shift domain material point method for solids in the finite deformation range, special thematic issue for Meshfree and Particle Methods for Modeling Extreme Loadings, Computational Particle Mechanics, doi: 10.1007/s40571-019-00239-y, 2019. [PDF]
- C. Liu, W.C. Sun, ILS-MPM: an unbiased implicit level-set-based material point method for frictional particulate contact mechanics of deformable particles, Computer Methods in Applied Mechanics and Engineering, accepted, doi:10.1016/j.cma.2020.113168, 2020. [PDF]
- R. Ma, W.C. Sun, A finite micro-rotation material point method for micro-polar solid and fluid dynamics with three-dimensional evolving contacts and free surfaces, Computer Methods in Applied Mechanics and Engineering, doi:10.1016/j.cma.2021.114540, 2022.
- M. Xiao, W.C. Sun, C. Liu, DP-MPM: Domain partitioning material point method for evolving multi-body thermal-mechanical contacts and fragmentation, Computer Methods in Applied Mechanics and Engineering, 385:114063, doi:10.1016/j.cma.2021.114063, 2021. [Video]
"Stress-chain" of granular assembles simulated via LS-MPM
|
Contact stress simulated via LS-MPM
|
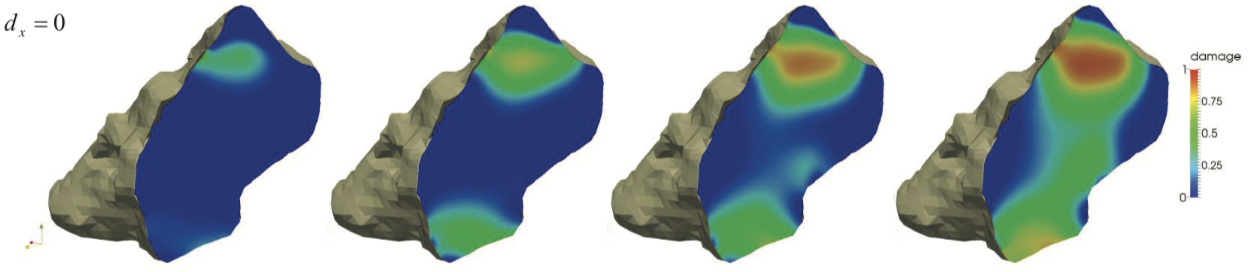
Particle damage occurs during indentation simulated by a nonlocal damage model. Note that classical DEM cannot recover any stress field or energy flux information near the singular tip and hence cannot accurately predict the propagation of crack and crack branching consistent with fracture mechanics theory.
Micromechanics of wetted and dry porous materials
|
The reason we can build sand sculpture is due to the presence of liquid bridges among particles that are otherwise cohesionless. From a micro-mechanical perspective, liquid bridge and the solid grains are two interacting networks that transmits force and moment. As a result, when subjected to external loadings, granular assemblies with a a very small volume fraction of water can behave profoundly different than the dry counterpart. The objective of this research is to predict how this solid-fluid interaction in grain scale affect the macroscopic outcomes. This research is important for a number of engineering applications, including landslides, vehicle mobility and seismic signature of earth materials.
Currently, the research team is working on extending the framework to analyze granular materials beyond the pendular regime using two-phase flow model to simulate the air-water-solid interaction in the void space. To make the multiscale model more accessible, the research team has also studied and proposed new methodology to identify material parameters from micro-CT images. Through collaboration with Prof. Salager and his colleagues, we construct inverse problem that takes account both the macroscopic constitutive responses and micro-structural attributes captured by micro-CT and digital image correlation in the objective function. We are currently expanding this work to consider higher-order (e.g. micro-polar) kinematics obtained from micro-CT. Our preliminary results show that this method may provide a new way to introduce physical length scale directly from the grain particles, without the need to explicitly defining a nonlocal radius or other equivalent nonlocal length scale parameter. Originally written/last updated 1/31/2018. |
Evolution of degree of saturation of granular material in simulated suction controlled test (LEFT), and the coordination number time history of the same specimen (RIGHT) .
MircroCT images obtained from drained triaxial compression test (cf. Wang et al. IJMCE, 2016)
|
Team Members:
- Kun Wang, 09/2014 - 09/2018
- Hyoung Suk Suh, 09/2018 - current
- Zeyu Xiong, 09/2020 - current
- Qing Yin, 03/2021 - current
- K. Wang, W.C. Sun, A micromechanical study on anisotropy of capillary stress in wetted granular matters, accepted, Journal of Engineering Mechanics, 2015.
- M.R. Kuhn, W.C. Sun, Q. Wang, Stress-induced anisotropy in granular materials: fabric, stiffness, and permeability, Acta Geotechnica, 2015.
- K. Wang, W.C. Sun, A semi-implicit discrete-continuum coupling method for fluid-saturated porous media at finite strain, Computer Method in Applied Mechanics and Engineering, 2016. [PDF]
- K. Wang, W.C. Sun, S. Salager, S. Na, G. Khaddour, Identifying material parameters for a micro-polar plasticity model via X-ray micro-CT images: lessons learned from the curve-fitting exercises, accepted, International Journal of Multiscale Computational Engineering, 2016. [DRAFT]
- W.C. Sun, T-F. Wong, Prediction of hydraulic and electrical transport properties of sandstone with multiscale lattice Boltzmann/finite element simulation on microtomographic images, International Journal of Rock Mechanics and Mining Science, 2018. [PDF]
Single and poly-crystal plasticity of rock salt for nuclear waste disposal
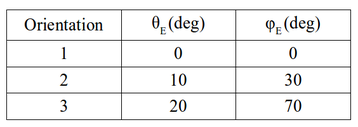
The thermo-hydro-mechanical behavior of rock salt is strongly depending on the microstructural attributes and micro-mechanics of the halite crystal that forms the rock salt. The desired engineering properties, such as the high thermal conductivity and the low permeability, and self-healing of rock salt are both attributed to the crystalline nature. In a geological system composed of salt or other crystalline rocks, individual grains or crystals are the fundamental building blocks that forms polycrystal assembles. The deformation of these assemblies are then related to both the deformation of each individual crystal and the grain boundary motion. As a result, thermo-mechanical responses at the microscopic scale, such as intergranular and intragranular fractures, as well as plastic slips, dislocation and the creeping due to precipitation may have significant implications for large scale engineering applications. While there are a multitude of macroscopic phenomenological model attempted to capture the complicated responses of rock salt, a multiscale approach that rightfully treated rock salt as polycrystalline materials may allow more robust predictions on the macroscopic anisotropic responses of rock salt in the finite deformation range. The goal of this work is to derive, formulate, predict, verify and validate polycrystalline model for rock salt and propose multiscale method to bridge the spatial and temporal scales.
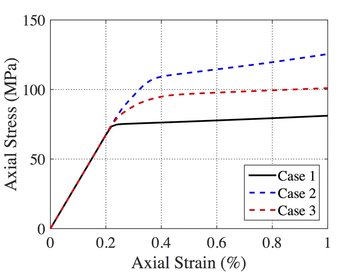Simulated responses of single crystal of halite of different orientations.
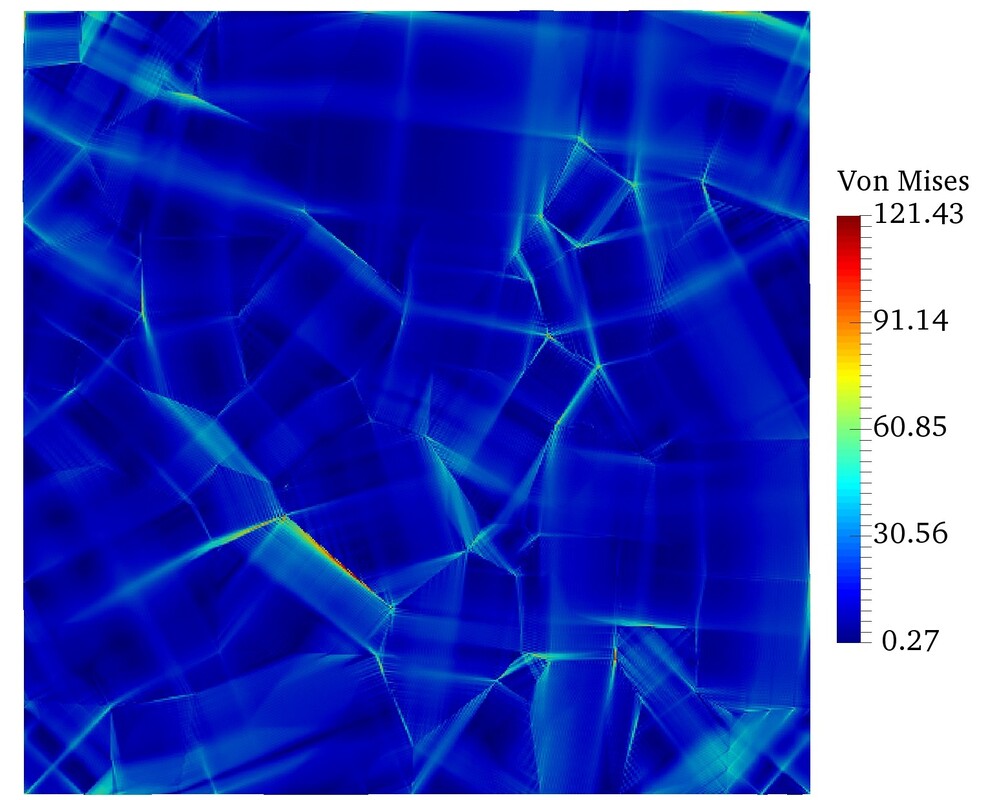
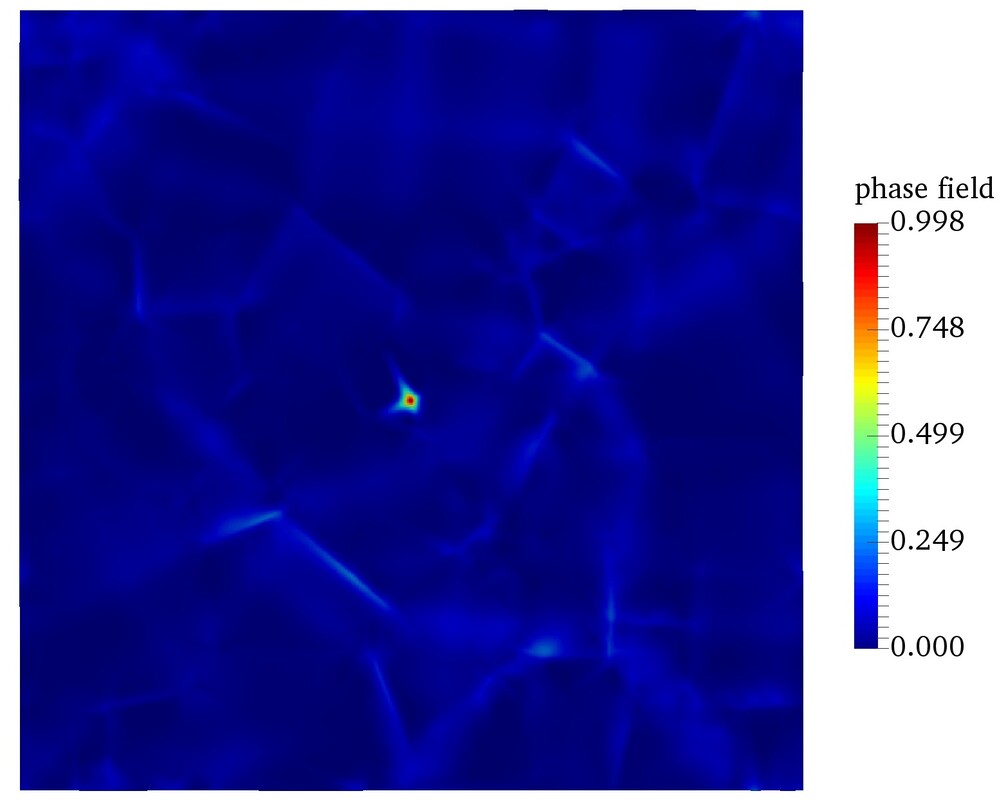
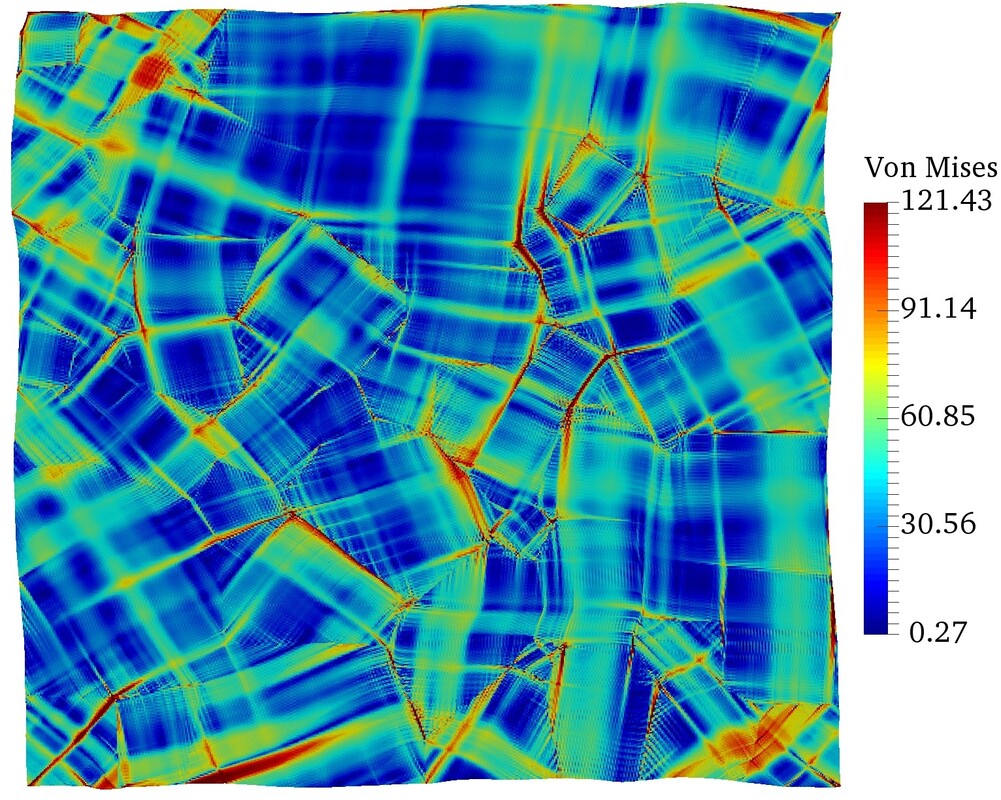
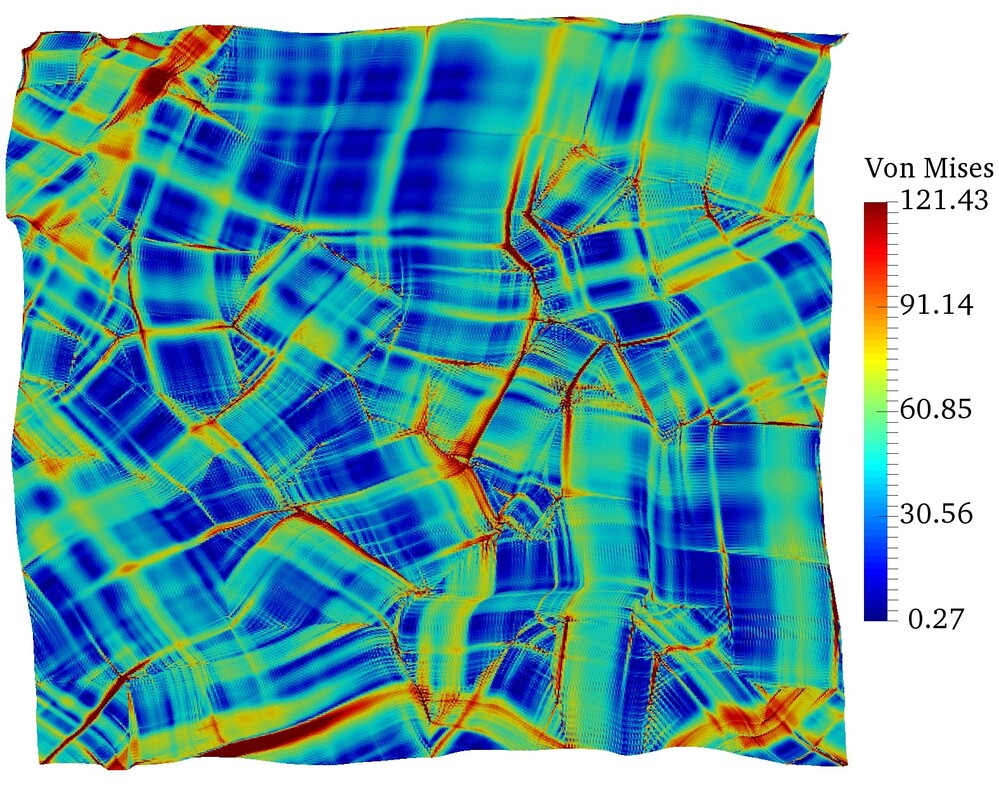
Currently, we have already completed the theoretical and algorithmic framework for small-strain crystal plasticity specifically designed for halite crystal in high pressure high temperature environment. In particular, we adopt the approach in which an elastic region in the stress space is defined and the sequence of the slip activation of the single crystal halite is considered. The analysis includes the thermo-mechanical creeping and micro-cracking for singly crystals under different loading conditions (orientation, loading rate, temperature, etc.). As a first step, we are interested at the anisotropic damage-plasticity of the slip system in Halite. Using the effective stress hypothesis, we employ a multi-phase-field model to capture the evolution of anisotropic damage of the single crystal, while using the crystal plasticity model to capture the plastic slip developed under different temperature and loading rate. The figures describe the axial stress-strain behavior under different orientations. The orientations of the single crystal of halite are described by Euler angles defining crystal axes (xc, yc, zc) relative to the reference coordinate system (x, y, z). Our next goal is to extend it to polycrystal problems and incorporate more mechanisms such as healing and migrations along grain boundaries.
Originally written/last updated 12/31/2018.
Originally written/last updated 12/31/2018.
Orientation 1
|
Orientation 2
|
Orientation 3
|
The equivalent plastic strain developed during biaxial compression test for single crystal of different orientations are shown above.
Simulation of crack growth in polycrystals under tensile loading
The anisotropic phase field that represents damage of the single crystal are shown above. In a more recent work, our postdoc research scientist Dr. Ran Ma has introduced two FFT solvers to simulate brittle fracture with strongly anisotropic fracture energy. By leveraging the global continuity of the Fourier series, we introduce a generalized frequency vector to compute the higher-order derivative required for the higher-order phase field. This method is compared with the multi-phase-field formulation where multiple phase field evolution equations and the mechanics problems are solved in a staggered update scheme. Results obtained from both phase field models are compared. The FFT provides a simple way to solve the problems without specific mesh generation and treatments to resolve the higher-order terms.
- SeonHong Na, 1/2017 - 12/2018
- Ran Ma, 1/2019-current
- S. Na, W.C. Sun, Computational thermomechanics of crystalline rock salt for nuclear waste disposal. Part I: a combined multi-phase-field/crystal plasticity approach for single crystal simulations, Computer Methods in Applied Mechanics and Engineering, 2018.
- R. Ma, W.C. Sun, FFT-based solver for higher-order and multi-phase-field fracture models applied to strongly anisotropic brittle materials and poly-crystals, Computer Methods in Applied Mechanics and Engineering, accepted, 2019.
- R. Ma, W.C. Sun, Computational thermomechanics for crystalline rock. Part II: chemo-damage-plasticity and healing in strongly anisotropic polycrystals, under review.
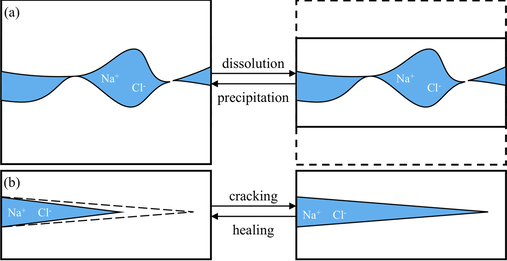
In a more recent work, our postdoc research scientist Dr. Ran Man extends the FFT solver to incorporate the effect of healing, the precipitation creeping due to the transport, the permeability evolution and the crystal plasticity of polycrystalline salt (see right Figure). To capture the healing process that often begins at the crack tips, an indicator function is used to locate the crack tip and the interfacial diffusion is captured explicitly along the grain boundaries to faithfully capture the solution-precipitation creeping of polycrystals. The resultant rate-dependence and the effect the evolution of damage and plastic deformation are shown below. A manuscript will be submitted in the near future (est. Oct 2019) to document this work.
|
|
|
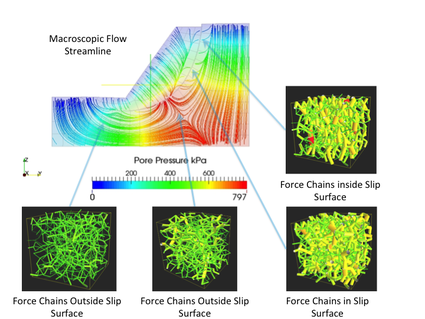
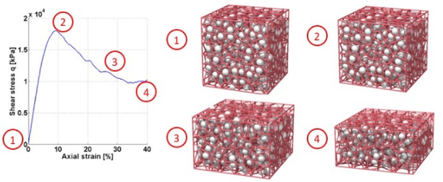
Environmental driven fractures and compaction banding of porous brittle solids
|
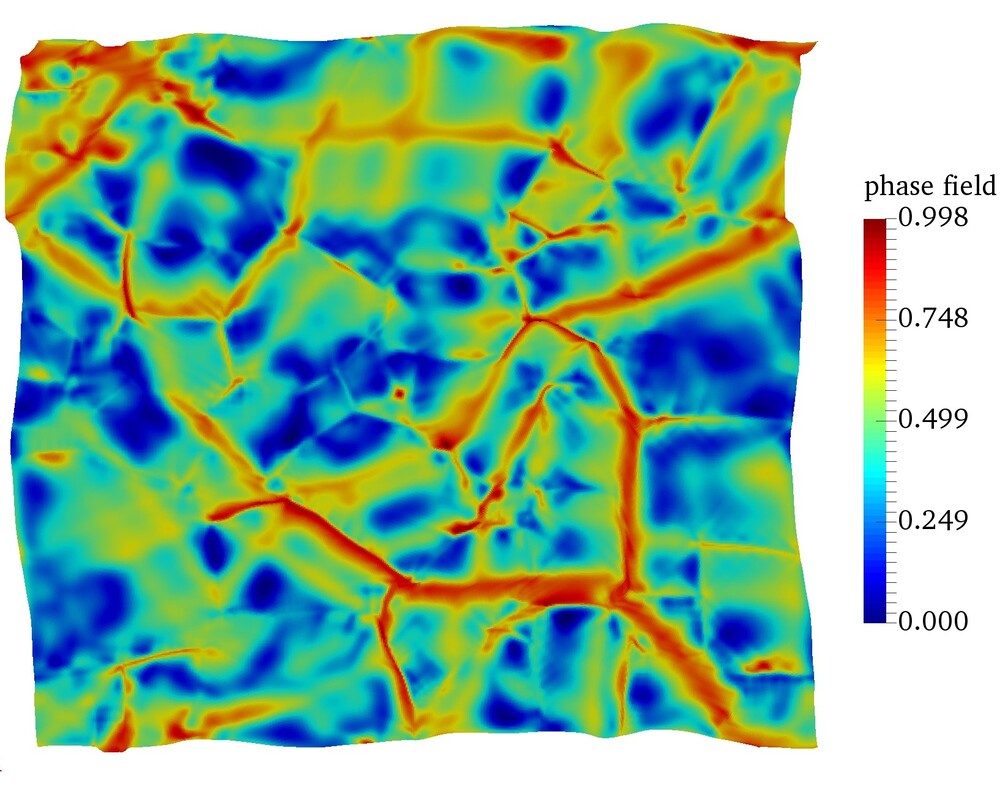
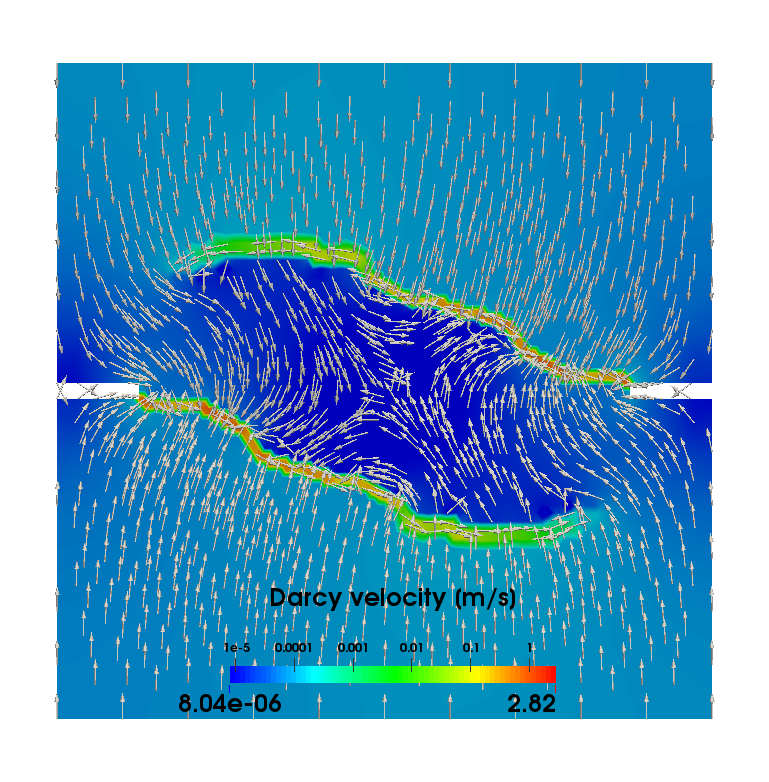
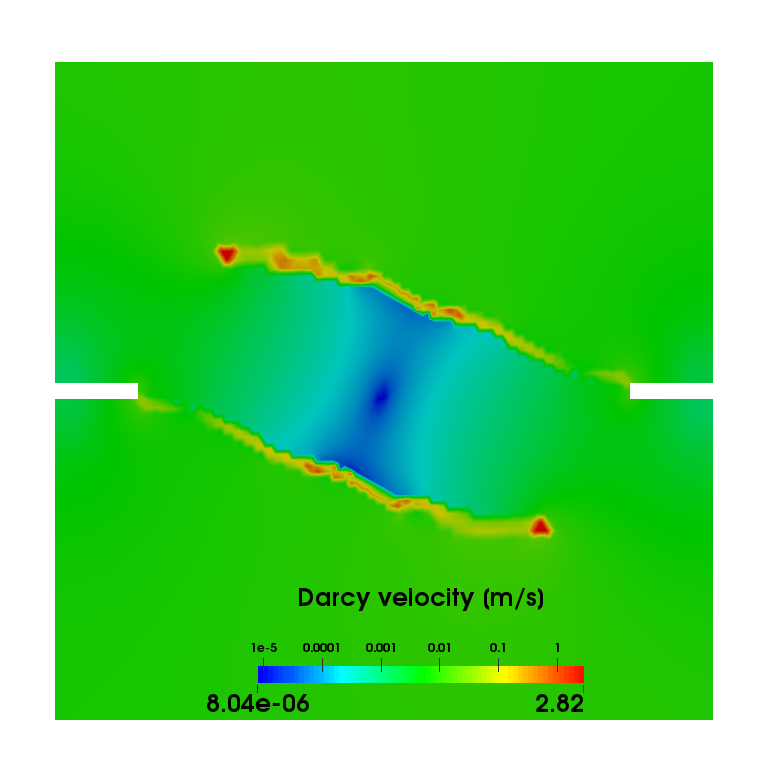
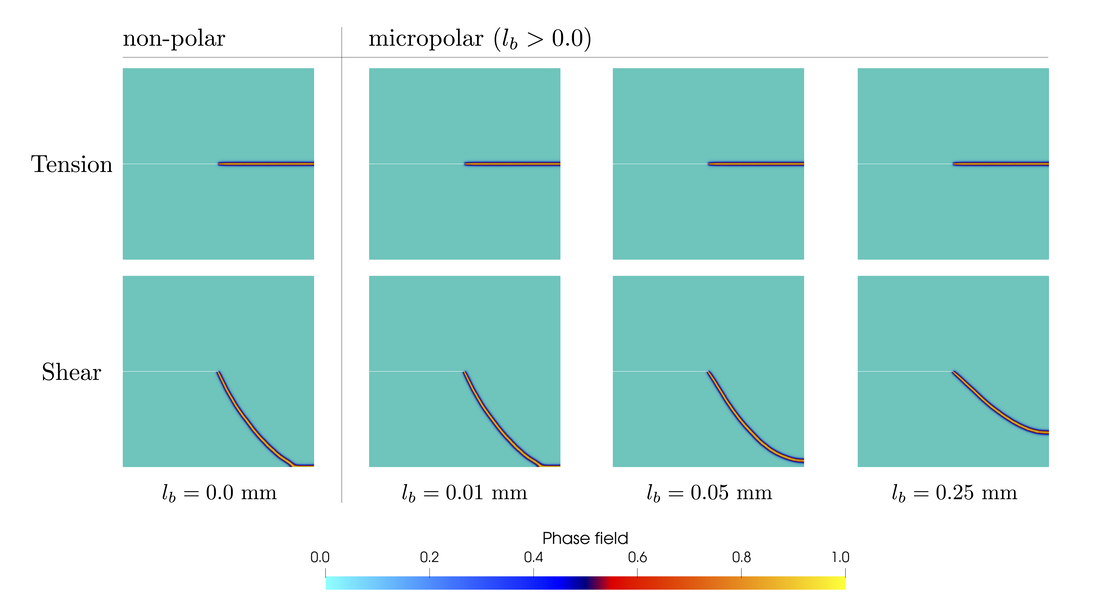
The goal of this study is to analyze the solid-fluid interaction of cohesive-frictional and brittle materials across length scale. Our goal is to analyze the relationships between hydraulic properties (such as permeability, hydraulic and mechanical apertures) and microstructural attributes, (such as connectivity of force chain and bonding strengths) before and after the onset of fractures. At the grain-scale level, We apply graph theory to unveil how the topology and geometry of force chain and flow network leads to the complex macroscopic outcome, such as fracturing and strain localization.
A recent extension of work includes the derivation of a new variational formulation that incorporate the eigen-fracture model for fluid-driven fracture problem and the introduction of eigen-deformation mode to simulate the propagation of compaction band and shear-enhanced compaction band as a Mode I anti-crack. We also propose a new way to compute the hydraulic aperture from the nonlocal phase field fracture and eigen-fracture model and validate the numerical simulations with Nooru-Mohamed tests (see Figure on the RHS). Originally written/last updated 12/31/2018. Team Members:
|
Pore pressure gradient induced by propagating fractures.
Micropolar phase field model that exhibits size effect in both elastic and damage regimes
Phase field modeling of the chemo-driven healing process of cracks in polycrystals
|
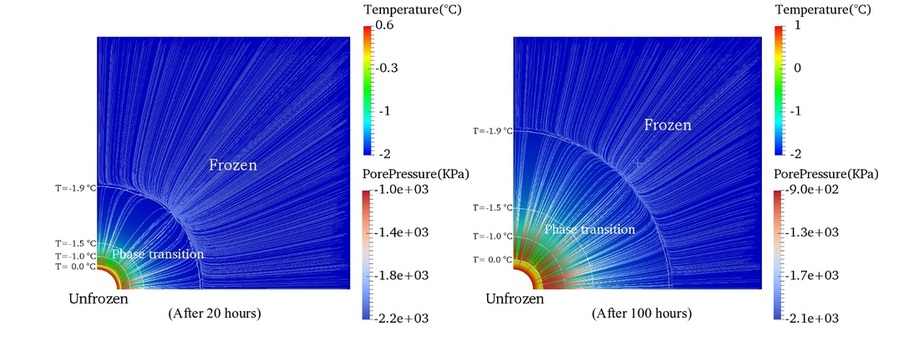
Computational modeling of frozen porous media at finite strain
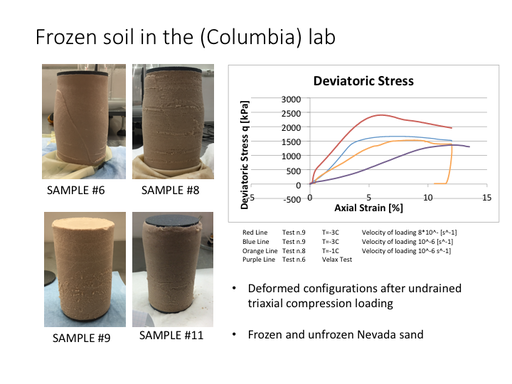Deformed frozen soil (Nevada sand) specimen taken after the triaxial compression load at undrained condition
Freeze-thaw cycle of porous media can lead to significant damage in concrete or pavement. Interestingly, due to the surface energy difference, water thin-film often develops in between solid grains and ice crystal. At a sufficiently large scale in which RVE exists, the frozen porous media can be regarded as a three-phase mixture in which ice, water and solid grains all occupied a fraction of volume. However, depending the temperature and pressure, the ice and water constituents may have phase change and that leads to mass exchange. In particular, the thawing of the ice crystal in frozen soil may lead to a very weak and wet soil layers that are likely to undergo large deformation. Nevertheless, the finite strain behavior of the frozen soil with unfrozen water flowing inside the pores is not well understood. The goal of this study is to formulate a new mathematical framework to capture the mechanics of the frozen porous media that undergoing phase transition at the geometrical nonlinear regime. A climate-controlled triaxial apparatus will be utilized to study the thermo-hydro-mechanical coupling effect of the frozen soil. A preliminary study has been conducted by PhD student SeonHong Na to study the strain localization occurred in frozen soil at finite strain. This work was presented at Engineering Mechanics Institute at Nashville in which SeonHong has won the 2nd place in the best paper competition.
Originally written/last updated 12/31/2018.
Team Members:
Originally written/last updated 12/31/2018.
Team Members:
- SeonHong Na, 09/2015 - 12/2018 (now assistant professor at McMaster University)
- Alessandro Milleri, 09/2018 - current
- Hyoung Suk Suh, 09/2018 - current
- Qing Yin 03/2021 - current
- S. Na, W.C. Sun, Computational thermo-hydro-mechanics for multiphase freezing and thawing porous media in the finite deformation range, Computer Methods in Applied Mechanics and Engineering, 2017. [URL]
- H. Suh, W.C. Sun, Asynchronous phase field fracture model for porous media with thermally non-equilibrated constituents, Computer Methods in Applied Mechanics and Engineering, doi:10.1016/j.cma.2021.114182, 2021. [Preprint]
- H. Suh, W.C. Sun, Multi-phase-field microporomechanics model for simulating ice lens growth and thaw in frozen soil, under review.
Finite Element simulations of Injecting unfrozen liquid in frozen ground at finite strain regime.
Nonlocal and higher-order continuum-discrete Coupling for porous media
|
We propose a nonlocal multiscale framework that couples grain-scale discrete element simulations with a macroscopic continuum-based finite element model. The upshot of this nonlocal coupling model is that it retains the simplicity and efficiency of the continuum-based finite element model, while possessing the original length scale of the granular system. In Liu et al. 2015, the collective mechanical responses of particles at material points are homogenized via a staggered nonlocal operator applied on local regions such that the multi-scale simulations exhibit no pathological mesh dependence. However, the local regions must be sufficiently large in order to collect enough integration points to compute the nonlocal strain in the finite element model.
As a result, the research group has made other attempts to incorporate length scales, such as introducing second-order homogenization techniques. For instance, one may consider the incorporation of the higher-order kinematics, such as micro-rotation, micro-stretch and micro-torsion, and formulate a Hill-Mandel Lemma with more one one energy-conjugated pairs. Team Members:
|
Comparison between DEM-FEM and pure DEM simulations.
Void space configuration changes due to grain rearrangement simulated by DEM in DEM-FEM coupling scheme.
High-order homogenization of granular materials
|
Configurational Poromechanics with Lie-algebra internal variable recovery
Error due to projections of element in Lie group by interpolating polynomial functions (TOP), and interpolating via Lie Algebra
The motivation of this research is to use the configuration force on poromechanics problems to help solving some of the common problems encountered in modeling material failures. For instance, configurational force can be used as a criterion to detect fracture in brittle materials or used as a criterion to detect needs for re-meshing. While this ability has been exploited since the 1990s, the application to poromechanics problems is relatively rare.
To demonstrate this idea, we are currently working on a critical state plasticity model that exhibits size-dependent anisotropy. Because of this size-dependent effect, re-meshing is a helpful tool to make simulations results more efficient. Typically, re-meshing of problems dealing with path-dependent models is difficult due to (1) the need to mapping history variables and (2) the establishment of new equilibrium after the re-meshing. To resolve (1), we use Lie algebra. As demonstrated previously in Wang and Sun, CMAME, 2018 andd earlier in Mota et al. 2014, the quality of projecting tensorial quantity that represent the history of the material is the key for any adaptions. The fields in the formulation are the deformation mapping, the target or mapped internal variables and a Lagrange multiplier that enforces the equality between the source and target internal variables. This formulation leads to an L2 projection that minimizes the distance between the source and target internal variables as measured in the L2 norm of the internal variable space.
To ensure that the target internal variables remain in their original space, their interpolation is performed by recourse to Lie groups, which allows for direct polynomial interpolation of the corresponding Lie algebras by means of the logarithmic map. Once the Lie algebras are interpolated, the mapped variables are recovered by the exponential map, thus guaranteeing that they remain in the appropriate space.
Team Members:
To demonstrate this idea, we are currently working on a critical state plasticity model that exhibits size-dependent anisotropy. Because of this size-dependent effect, re-meshing is a helpful tool to make simulations results more efficient. Typically, re-meshing of problems dealing with path-dependent models is difficult due to (1) the need to mapping history variables and (2) the establishment of new equilibrium after the re-meshing. To resolve (1), we use Lie algebra. As demonstrated previously in Wang and Sun, CMAME, 2018 andd earlier in Mota et al. 2014, the quality of projecting tensorial quantity that represent the history of the material is the key for any adaptions. The fields in the formulation are the deformation mapping, the target or mapped internal variables and a Lagrange multiplier that enforces the equality between the source and target internal variables. This formulation leads to an L2 projection that minimizes the distance between the source and target internal variables as measured in the L2 norm of the internal variable space.
To ensure that the target internal variables remain in their original space, their interpolation is performed by recourse to Lie groups, which allows for direct polynomial interpolation of the corresponding Lie algebras by means of the logarithmic map. Once the Lie algebras are interpolated, the mapped variables are recovered by the exponential map, thus guaranteeing that they remain in the appropriate space.
Team Members:
- SeonHong Na, 09/2017-12/2018 (now assistant professor at McMaster University)
- Kun Wang, 09/2015-9/2019
- Eric Bryant, 09/2017-08/2020
- S. Na, E.C. Bryant, W.C. Sun, A configurational force for adaptive re-meshing of gradient-enhanced poromechanics problems with history-dependent variables, Computer Methods in Applied Mechanics and Engineering, doi:10.1016/j.cma.2019.112572, 2019.
- A. Mota, W.C. Sun, J.T.Ostein, J.W. Foulk III, K.N. Long, Lie-Group interpolation and variational recovery for internal variables, Computational Mechanics, 52:1281-1299, doi:10.1007/s00466-013-0876-1, 2013. [PDF] [Bibtex]
Re-meshing of poromechanics problem with configurational force.
Concurrent and sequential coupling of multiphysics problems at finite strain
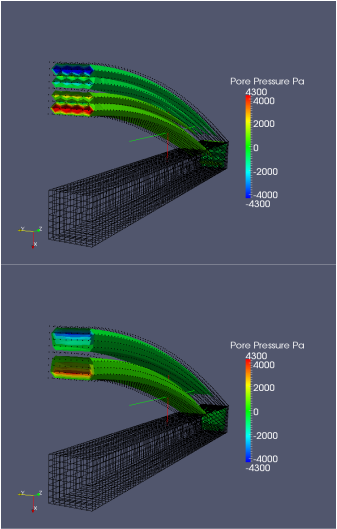Pore pressure distribution of poro-elastic beam obtained by stabilized (BOTTOM) and standard (TOP) finite element.
We design and implement of iterative sequential and monolithic schemes to simulate a variety of multiphysics problems. Our objective is to derive general framework to simulate a variety of multi-physics processes that involve solid mechanics coupled with hydraulic, heat and chemical transport. Since conventionally equal-order finite element space often lead to numerical instability, we formulated adaptively stabilized schemes that eliminate spurious oscillations while preserving correct boundary layer thickness. In addition, a critical state plasticity model is being implemented to replicate the constitutive responses of sands under various fluid saturation condition.
We have recently written a review on the thermo-hydro-mechanical problem for the September issue of the imechanica journal club. The full text can be found at http://imechanica.org/node/17096.
Team Members:
We have recently written a review on the thermo-hydro-mechanical problem for the September issue of the imechanica journal club. The full text can be found at http://imechanica.org/node/17096.
Team Members:
- SeonHong Na, 09/2014 - 12/2018 (now assistant professor at McMaster University)
- Kun Wang, 07/2014 - current
- Eric C. Bryant, 09/2016 - current
- Federica Ronchi (visiting student from Università degli Studi di Perugia)
- O.I. Ulven*, W.C. Sun, A two-way coupling dual-graph lattice model for fluid-driven fracture, International Journal for Numerical and Analytical Methods in Geomechanics, 2018.
- S. Na, W.C. Sun, Thermo-hydro-mechanical coupling effects on dynamic wave propagation in a fully saturated softening porous medium, International Journal for Numerical and Analytical Methods in Geomechanics, doi:10.1002/nag.2505, 2016. [PDF]
- W.C. Sun, A Stabilized finite element formulation for monolithic thermo-hydro-mechanical simulations at finite strain, International Journal for Numerical Methods in Engineering, 2015.
- W.C. Sun, Q. Chen, J.T. Ostien, Modeling hydro-mechanical responses of strip and circular footings on saturated collapsible geomaterials, Acta Geotechnica, 2014.
- W.C. Sun J.T. Ostien, A. Salinger, A stabilized assumed deformation gradient finite element formulation for strongly coupled poromechanical simulations at finite strain, International Journal for Numerical and Analytical Methods in Geomechanics, 2013.
- W.C. Sun, An unified method to predict diffuse and localized instabilities in sands, Geomechanics and Geoengineering, 8(22):65-75, 2013.
Multi-model concurrent analysis with domain overlapping method
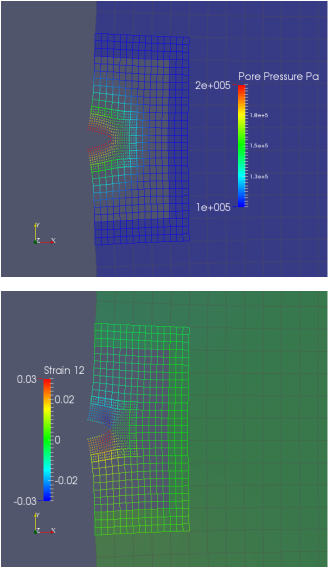Multiphysics Domain coupling model across three length scales (single crack - specimen - field ).
The macroscopic mechanical failures, such as fracture and strain localization, are to a large extent determined by physical processes which occur at a scale several orders of magnitude smaller than the macroscopic observation. In order to model this inherent multiscale character efficiently, models designed specifically for macro- and micro-scales are often blended together in a handshake domain. Bridging the multi-model, multi-scale domain is, however, not a trivial problem. Spurious wave reflection, ghost force, artificial energy dissipation/increase, mesh dependence and incompatible deformation modes are all challenges persisted for this multi-model approach. To allude these drawbacks, we introduced an inf-sup stable domain overlapping method and extended it for large deformation, path-dependent plasticity and poroplasticity problems. To circumvent mesh dependence due to the loss of ellipticity, we introduced nonlocal plasticity model and concurrently coupled it with classical continuum model for far-field responses. Such a numerical treatment allows one to concentrate computation resource in a highly localized region of interest and thus significantly increases efficiency.
Graduate student(s):
Graduate student(s):
- Kun Wang, 09/2015-current
- SeonHong Na, 09/2015-current
- Eric Bryant, 09/2016-current
- Sun, Mota, A multiscale overlapped coupling formulation for large deformation strain localization, Computational Mechanics, 2015.
- W.C. Sun, Z. Cai, J. Choo, Mixed Arlequin method for multiscale poromechanics problems, International Journal for Numerical Methods in Engineering, 2016.
Multi-scale hierarchical analysis with geometrical enhancements from microstructures: material parameter identification across length scales
|
Analysis from our studies shows that hierarchical multi-scale flow simulation that neglects pore connectivity may lead to significant error and reduce efficiency. As a result, we introduced a new method based on graph theory to extract geometrical attributes from X-ray CT images. Information of geometrical attributes is used to improve the coupling among the pore-scale lattice Boltzmann and field scale finite element simulations. By applying this improved scheme, my collaborators and I quantified the relations between grain crushing and hydraulic property changes. Such information is important for analyzing material bifurcation that leads to fracture and deformation band formation. This work helps improving our understanding on mechanical/hydraulic interactions of solid skeleton and pore-fluid, which is highly relevant to carbon dioxide storage, nuclear waste management and reservoir management.
Team Members:
|
Microstructures of sandstone reproduced from a 3D printer.
Flow simulations on CT images
|
Estimating co-seismic deformation with combined deterministic-stochastic Monto Carlos simulations
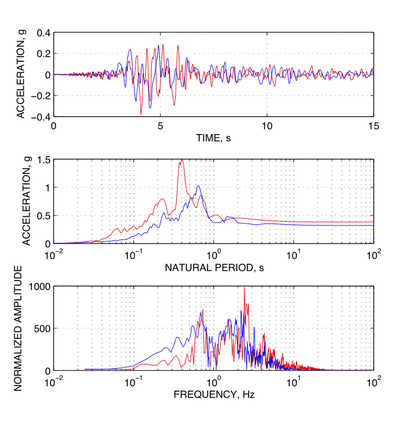Simulated vs. recorded acceleration time history
My previous research project at Stanford University focuses on estimating co-seismic deformation during the 1989 Loma Prieta earthquake. In this study, Professor Borja and I investigated the influence of noise on the estimated co-seismic deformation using a combined deterministic-stochastic approach. We compare the classical equivalent linear method with a deterministic nonlinear finite element scheme with stochastic input. By quantifying the impact of noise and baseline offset presented in the input ground motion, we conclude that the sediment deformation may have affected the accuracy of the previously back-figured fault rupture mechanism.
Related Publications:
Related Publications:
Our research at Columbia is proudly sponsored by:
|
|
|
|
|
|
|
|
Disclaimer: Electronic copies of the preprints and articles are provided for convenience only. Before downloading, please check to make sure you have the right permission to download them from your institution. Unless specified otherwise, all materials are subjected to the Attribution 4.0 International (CC BY 4.0) license. If you use/incorporate/reproduce/borrow/develop any new derivation, data, figure, idea or information from this archive into your own work, either consciously or subconsciously, my students and I would greatly appreciate your decency by giving the appropriate credit where credit's due. We appreciate any comment, suggestion or critique, please contact wsun@columbia.edu. Thank you for your interest in our work.