Collaborative work with Sandia National Lab on design/planning of experiments with Kalman filter + deep reinforcement learning has published in Computational Mechanics

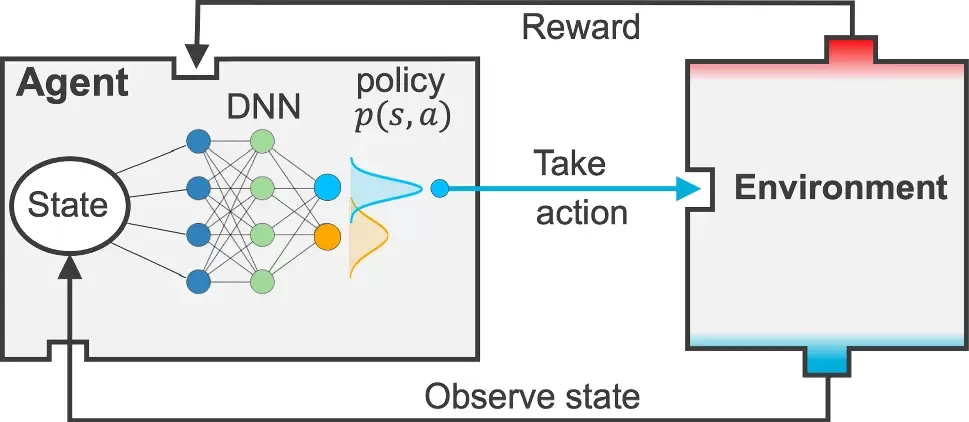
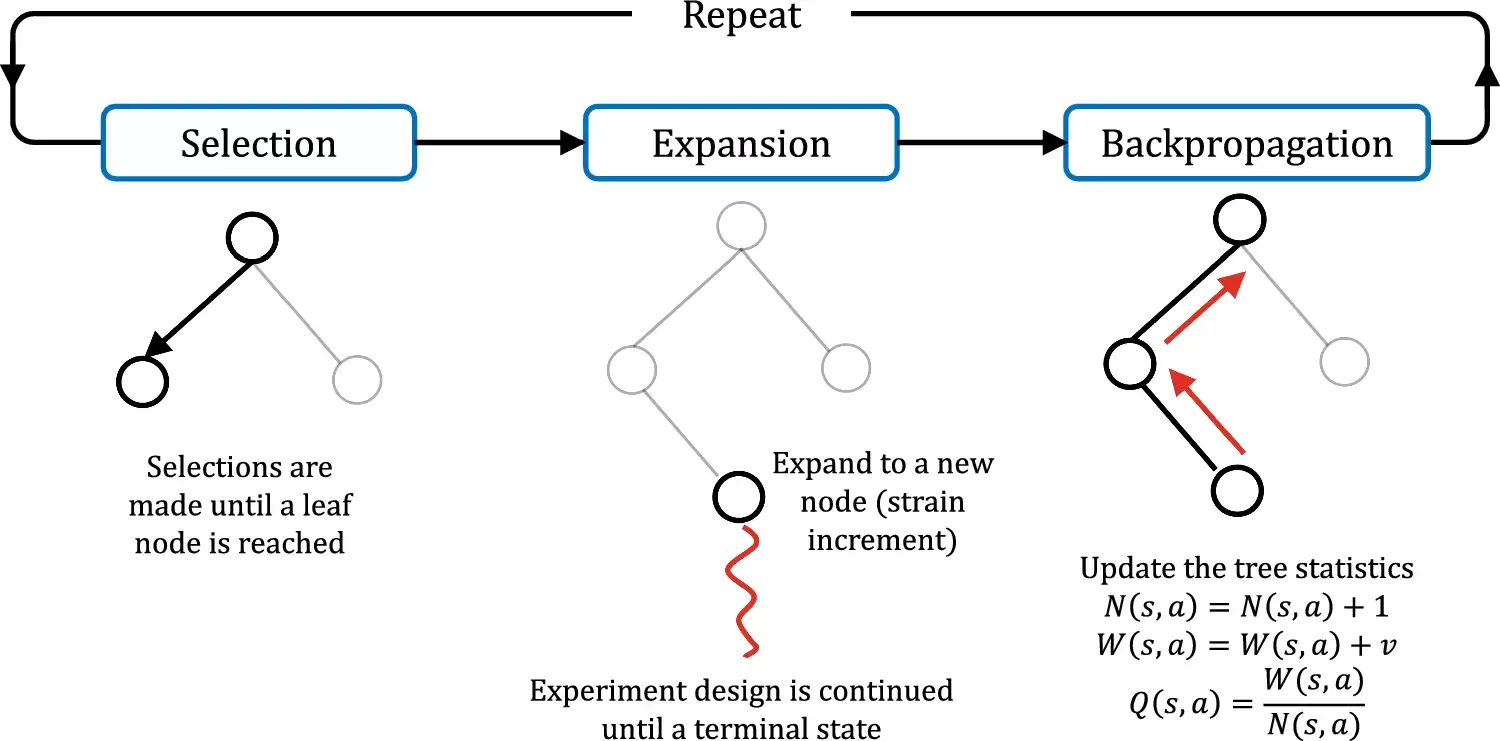
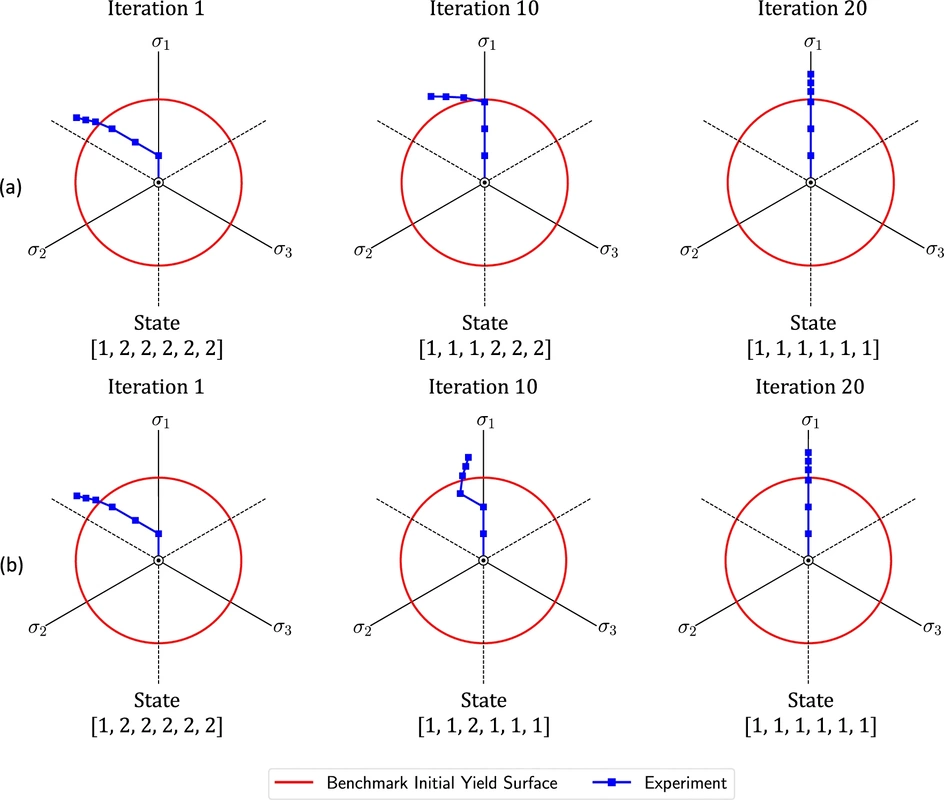
Our collaborative work with Sandia funded by the LDRD project led by Dr. Sharlotte Kramer has just published in the special issue "Machine Learning Theories, Modeling, and Applications to Computational Materials Science, Additive Manufacturing, Mechanics of Materials, Design and Optimization". The article is available in the Computational Mechanics website [URL].

Experimental data are often costly to obtain, which makes it difficult to calibrate complex models. For many models an experimental design that produces the best calibration given a limited experimental budget is not obvious. This paper introduces a deep reinforcement learning (RL) algorithm for design of experiments that maximizes the information gain measured by Kullback–Leibler divergence obtained via the Kalman filter (KF), see figure below.  

This combination enables experimental design for rapid online experiments where manual trial-and-error is not feasible in the high-dimensional parametric design space. We formulate possible configurations of experiments as a decision tree and a Markov decision process, where a finite choice of actions is available at each incremental step. 

Once an action is taken, a variety of measurements are used to update the state of the experiment. This new data leads to a Bayesian update of the parameters by the KF, which is used to enhance the state representation. In contrast to the Nash–Sutcliffe efficiency index, which requires additional sampling to test hypotheses for forward predictions, the KF can lower the cost of experiments by directly estimating the values of new data acquired through additional actions. In this work our applications focus on mechanical testing of materials. Numerical experiments with complex, history-dependent models are used to verify the implementation and benchmark the performance of the RL-designed experiments.