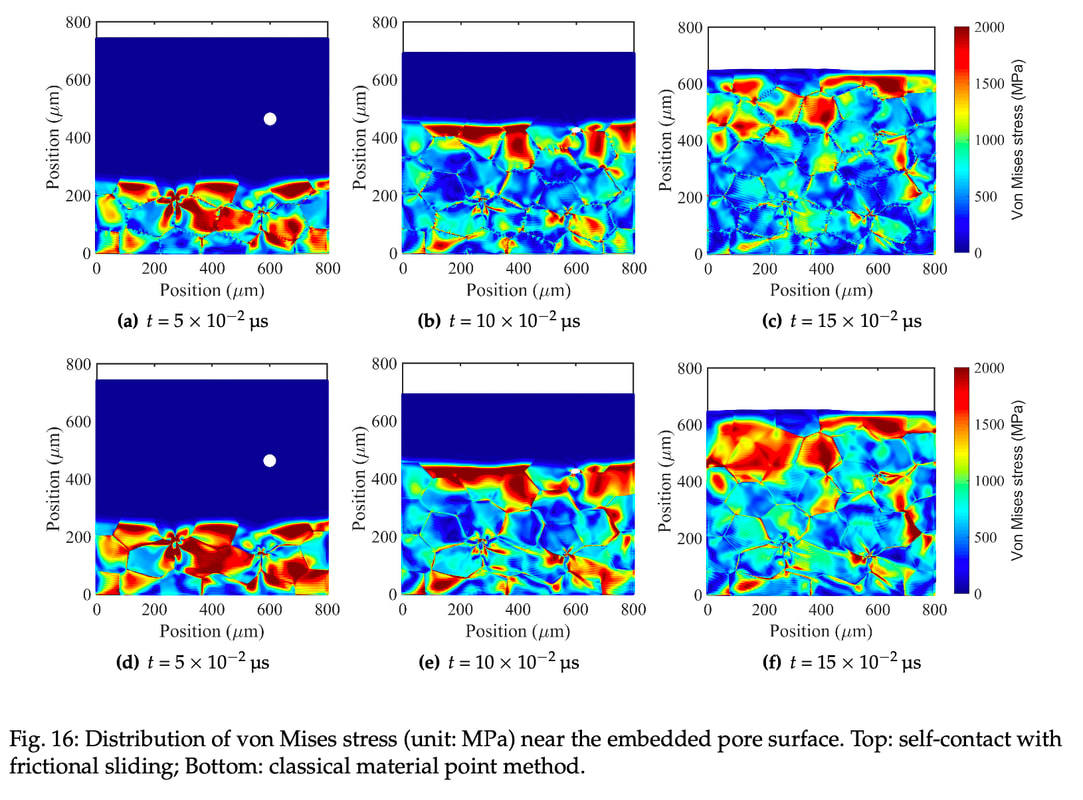
Authors: Ran Ma, WaiChing Sun, Catalin R. Picu,  Tommy Sewell
Preprint: [URL]
Abstract: Heterogeneous energetic materials (EMs) subjected to mechanical shock loading exhibit complex thermo-mechanical processes which are driven by the high temperature, pressure, and strain rate behind the shock. These lead to spatial energy localization in the microstructure, colloquially known as ``hotspots'',
where chemistry may commence possibly culminating in detonation. Shock-induced pore collapse is one of the dominant mechanisms by which localization occurs. In order to physically predict the shock sensitivity of energetic materials under these extreme conditions, we formulate a multiplicative crystal plasticity model with key features inferred from molecular dynamics (MD) simulations. Within the framework of thermodynamics, we incorporate the pressure dependence of both monoclinic elasticity and critical resolved shear stress into the crystal plasticity formulation. Other fundamental mechanisms, such as strain hardening and pressure-dependent melting curves, are all inferred from atomic-scale computations performed across relevant intervals of pressure and temperature. To handle the extremely large deformation and the evolving geometry of the self-contact due to pore collapse, we leverage the capabilities of the Material Point Method (MPM) to track the interface via the Lagrangian motion of material points and the Eulerian residual update to avoid the mesh distortion issue. This combination of features enables us to simulate the shock-induced pore collapse and associated hotspot evolution with a more comprehensive physical underpinning, which we apply to the monoclinic crystal beta-HMX. Treating MD predictions of the pore collapse as ground truth, head-to-head validation comparisons between MD and MPM predictions are made for samples with identical sample geometry and similar boundary conditions, for reverse-ballistic impact speeds ranging from 0.5 to 2km per second. Comparative studies are performed to reveal the importance of incorporating a frictional contact algorithm, pressure-dependent elastic stiffness, and non-Schmid type critical resolved shear stress in the mesoscale model.

Case 1: impact velocity = 320 meter per second 

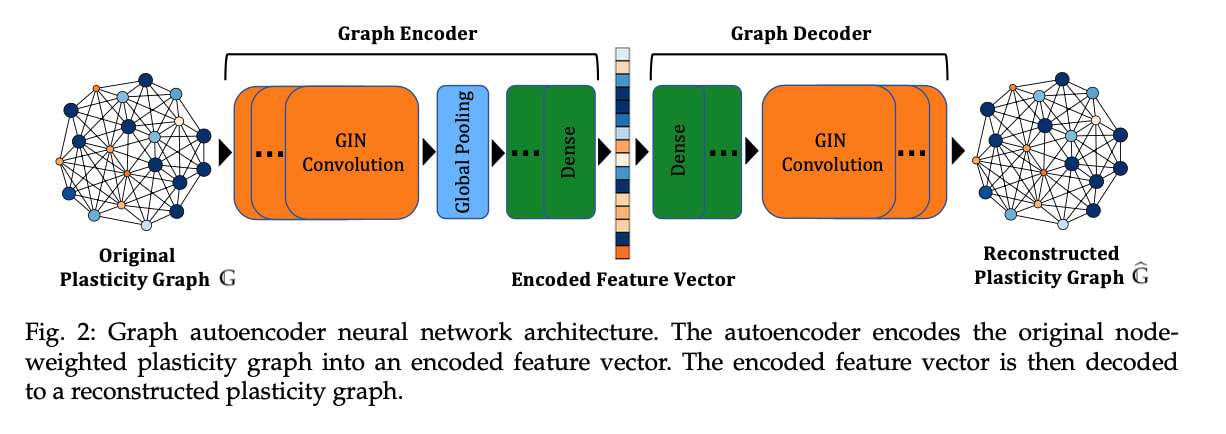
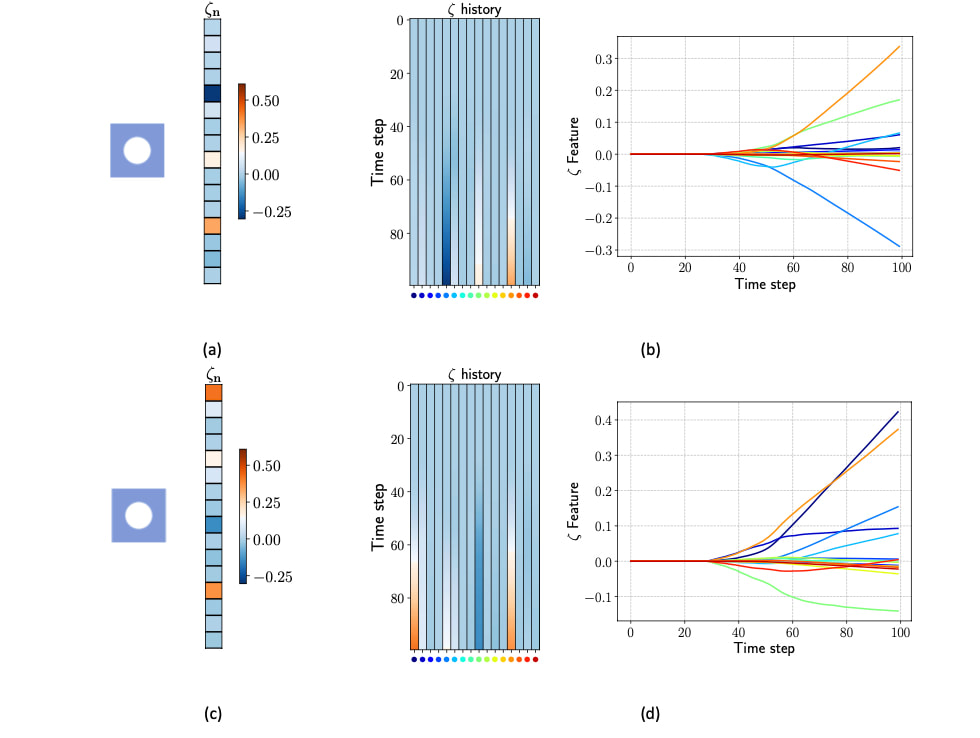
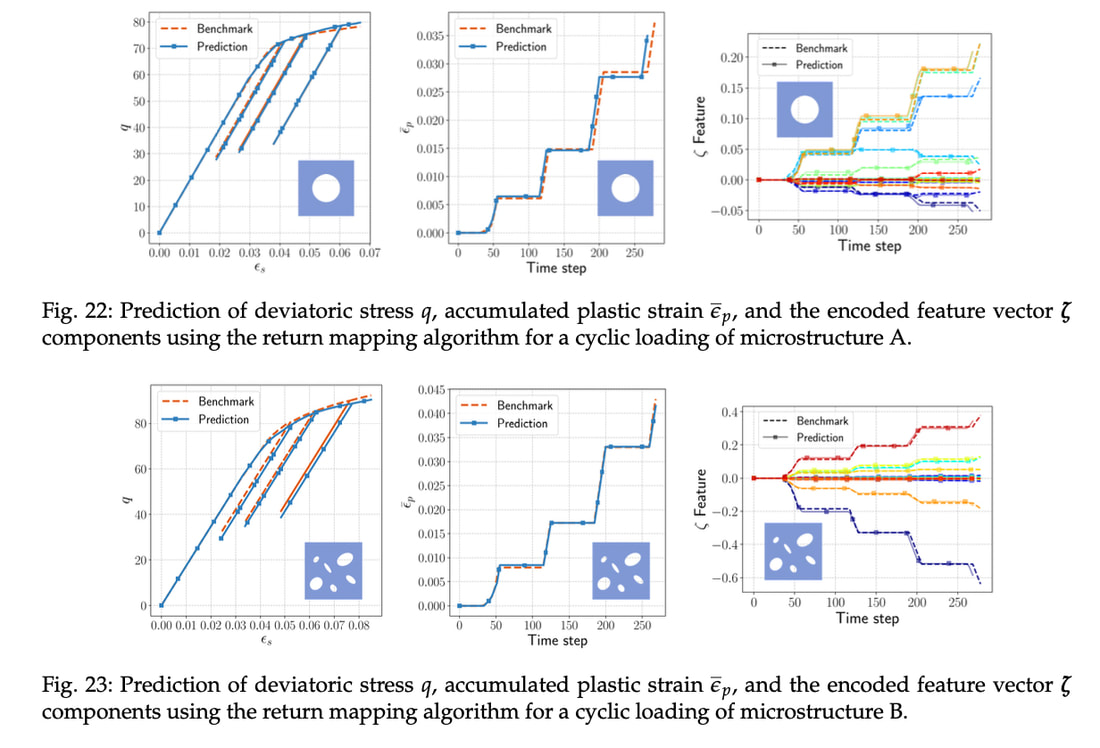
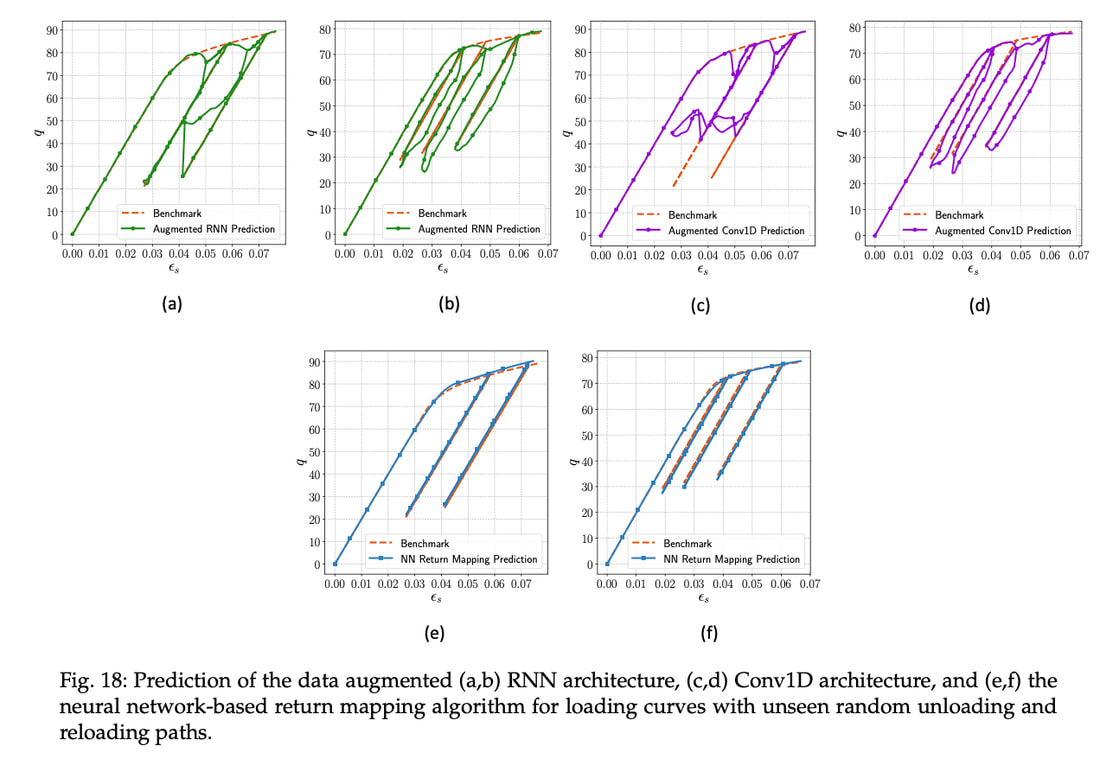
Generally speaking, reduced order modeling and constitutive modeling are considered different disciplines. In Part II of our research on geometric learning for computational Mechanics (see Part I here), we attempt to conduct these two very different ideas by using a graph isomorphism network to learn the low-dimensional representation of finite element solutions of microstructures.

​Then, instead of reconstructing the low-dimensional dynamics directly via a black-box approach, we use the macroscopic plasticity theory to create additional constraints (e.g., yield function consistency, plastic flow direction) such that the low-dimensional dynamics can be compatible with the macroscopic observations. ​

On the other hand, the autoencoder of the graph isomorphism network also gives us a chance to recast the element of the latent space as the internal variables of the plasticity model and therefore gives more direct and interpretable relations between microstructural deformation patterns and macroscopic plasticity. ​

Our results also indicate that the geometric learning approach may enable us to more explicitly understand the geometry of the data manifested by the shape of the yield function as a function of both stress and elements of latent space of plastic deformation of RVE. This understanding, in return, gives us the opportunity to recast the reduced order modeling problem that can be updated via a classical constitutive law that is now with internal variables that can b be encoded as a snapshot of finite element mesh. The resultant models is found to perform robustly in forward predictions with loading paths different from the training data, in thew sense that there is no spurious patterns that might exhibit in RNN or 1D convolutional NN (see below). 

Preprint posted at ResearchGate here. Part III of this series is under progress and will submit soon.