Our collaborative paper on MPM modeling of shock-induced pore collapse of poly-crystal energetic materials has been accepted by CMAME

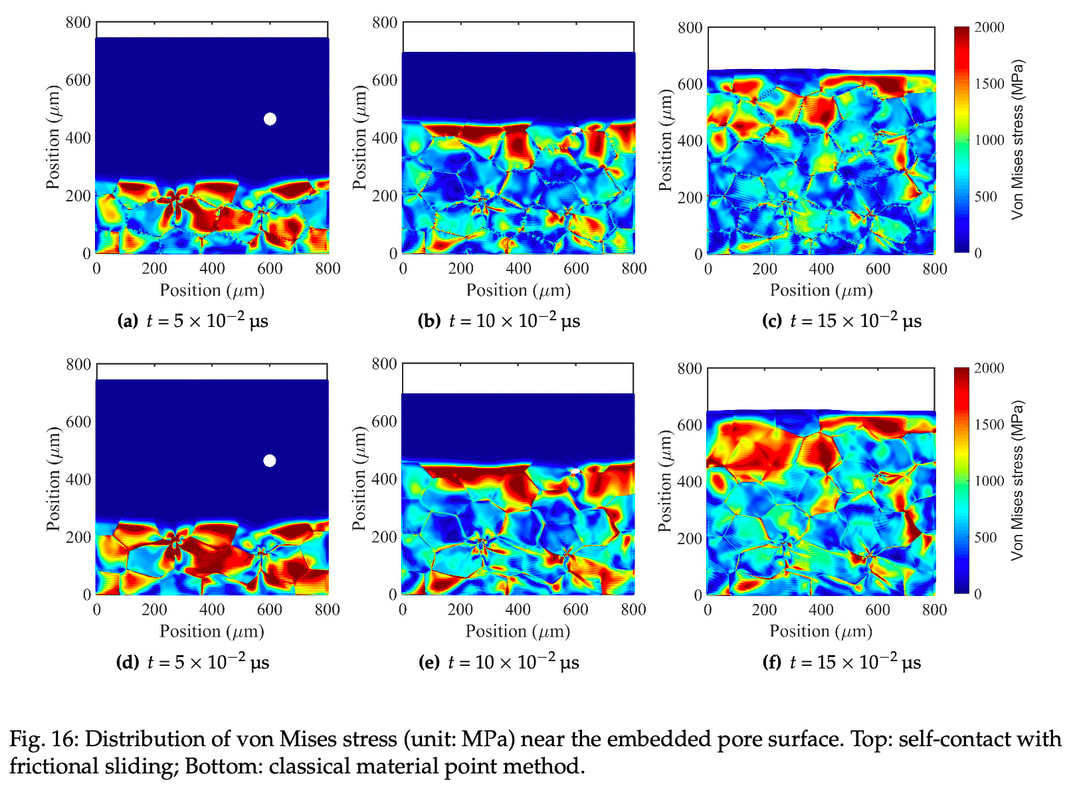
Authors: Ran Ma, WaiChing Sun, Catalin R. Picu,  Tommy Sewell
Preprint: [URL]
Abstract: Heterogeneous energetic materials (EMs) subjected to mechanical shock loading exhibit complex thermo-mechanical processes which are driven by the high temperature, pressure, and strain rate behind the shock. These lead to spatial energy localization in the microstructure, colloquially known as ``hotspots'',
where chemistry may commence possibly culminating in detonation. Shock-induced pore collapse is one of the dominant mechanisms by which localization occurs. In order to physically predict the shock sensitivity of energetic materials under these extreme conditions, we formulate a multiplicative crystal plasticity model with key features inferred from molecular dynamics (MD) simulations. Within the framework of thermodynamics, we incorporate the pressure dependence of both monoclinic elasticity and critical resolved shear stress into the crystal plasticity formulation. Other fundamental mechanisms, such as strain hardening and pressure-dependent melting curves, are all inferred from atomic-scale computations performed across relevant intervals of pressure and temperature. To handle the extremely large deformation and the evolving geometry of the self-contact due to pore collapse, we leverage the capabilities of the Material Point Method (MPM) to track the interface via the Lagrangian motion of material points and the Eulerian residual update to avoid the mesh distortion issue. This combination of features enables us to simulate the shock-induced pore collapse and associated hotspot evolution with a more comprehensive physical underpinning, which we apply to the monoclinic crystal beta-HMX. Treating MD predictions of the pore collapse as ground truth, head-to-head validation comparisons between MD and MPM predictions are made for samples with identical sample geometry and similar boundary conditions, for reverse-ballistic impact speeds ranging from 0.5 to 2km per second. Comparative studies are performed to reveal the importance of incorporating a frictional contact algorithm, pressure-dependent elastic stiffness, and non-Schmid type critical resolved shear stress in the mesoscale model.

Case 1: impact velocity = 320 meter per second 

Case 2: impact velocity = 840 meter per second 

---

Impact simulations for polycrystals