|
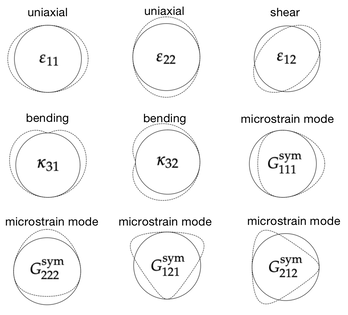
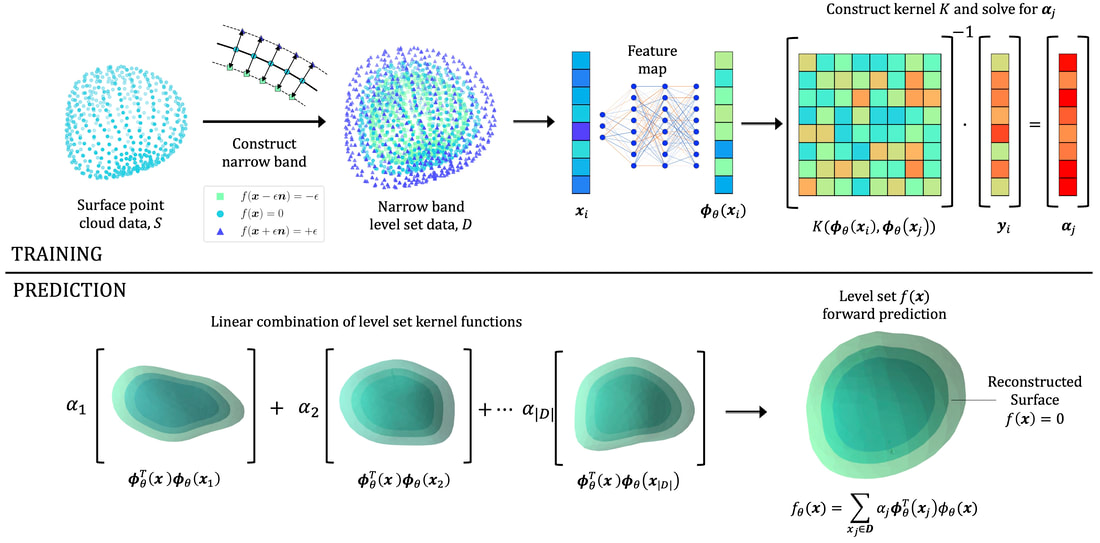
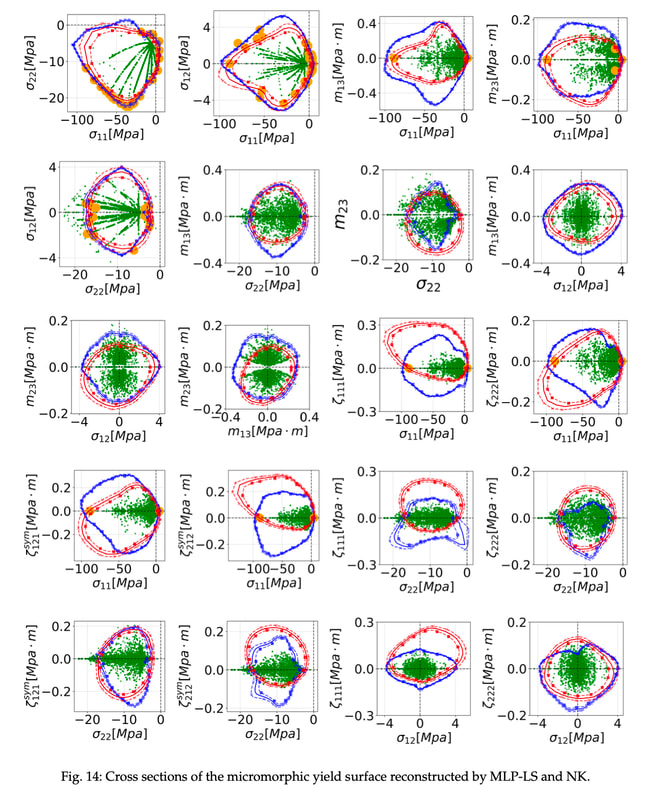
Most of the constitutive laws leverages symmetry to reduce the dimensionality of the models. A classical example is the assumption of material isotropy. However, there are cases in which the minimal dimension of the material models must increase to sufficiently describe the physics. An example is micropolar and micromorphic theories (see below). This increase of dimensionality makes it more difficult to derive constitutive laws manually, as our curve-fitting ability and sense of geometry often not extend beyond 3D. This paper introduces a neural kernel approach to generate high-dimensional micropolar and micromorphic plasticity models. Here we want to leverage the robustness and interpretability of the kernel method afforded by the feature space while generating a data-dependent kernel tailored to our specific need to capture the high-dimensional constitutive responses of the materials with complex internal structures. This treatment provides us with a unified data-driven approach to recognize the pattern of the data (through the data-dependent kernel), regardless of the data dimensions. Combined with a simple kernel ridge regression, we may generate a yield function of arbitrary input space dimensions without explicitly handcrafting the feature space. This trait is important for us to automate the process of generating yield surface from data of dimensions higher than 3, especially when data is sparse. The Figure below shows the learned micromorphic yield surface inferred from RVE projected onto 2D stress components. An interesting aspect we observe is that there could be multiple hypothesized yield surface fits the same data and they can be quite difference. Nevertheless, the feature space obtained from the kernels does seem to provide a regularization that lead to a more convex yield surface, which can be important to ensure thermodynamics consistency. More in-depth discussion can be found by the preprint [URL].
0 Comments
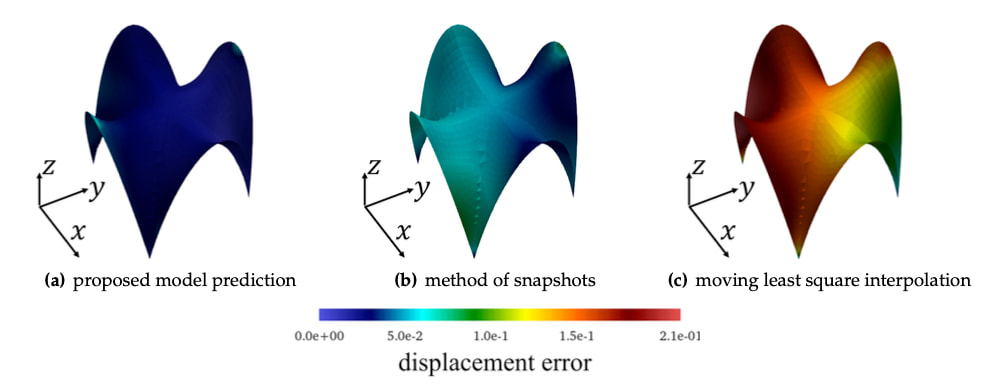
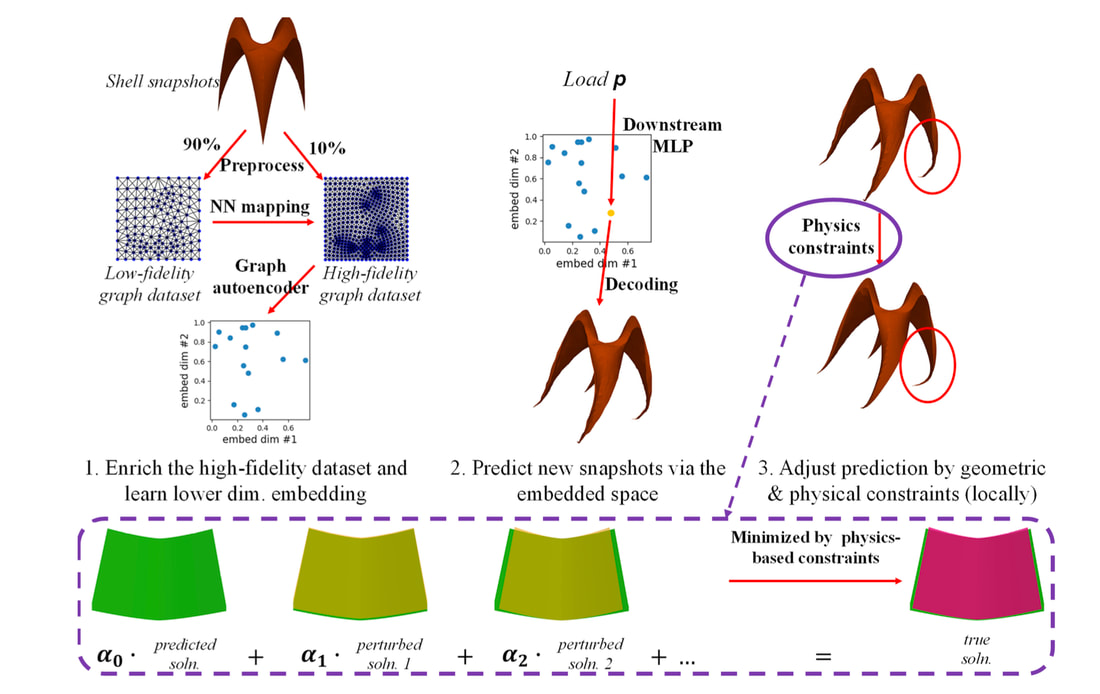
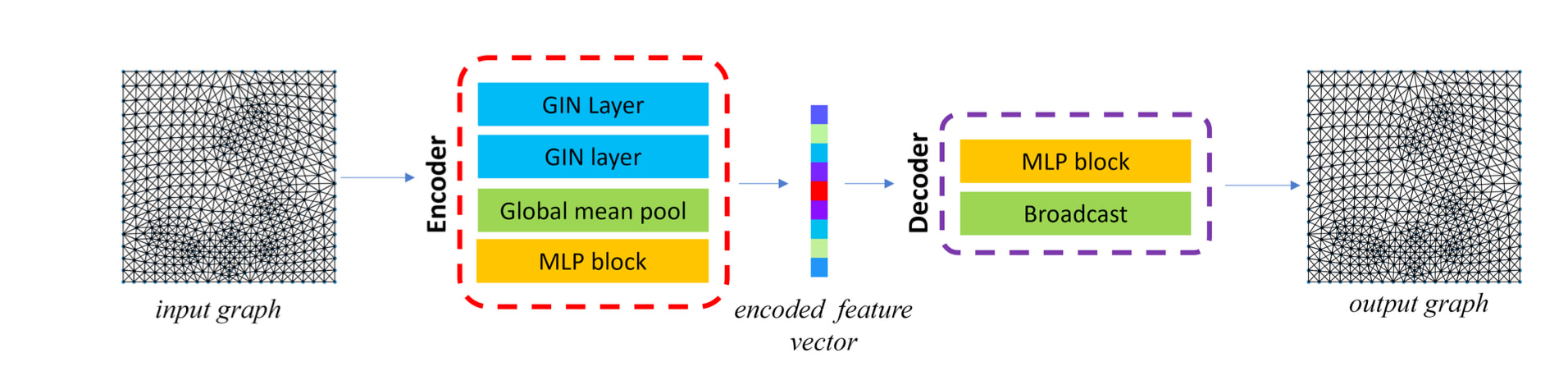
Classical finite element simulation often solves one boundary value problem at a time. However, for many engineering applications, a response surface for a family of boundary value problems is often needed to understand how a structure responds to a variety of external loadings. In principle, run multiple finite element simulations to populate the parametric space and then interpolate the responses. However, due to the high dimensionality of the problems (which is equal to the number of degrees of freedom), the traditional interpolation technique may lead to significant errors (see figure below for the Simo-Fox-Rifai shell). In this work, we have two goals. First, we want to introduce a technique in which we can use multi-resolution latent space deduced from the weighted graph of finite elements to predict high-fidelity finite element simulations with a mixture of low-fidelity data. Second, we want to introduce the physics constraints without introducing an underlying non-convex optimization (see the overall design). To achieve both goals, we use the graph isomorphism layer to construct an encoder for nonlinear dimensional reduction. While the graph isomorphism layer enables us to introduce message-passing mechanisms to aggregate information among the finite element nodes, the graph pooling and the multilayer-perceptron enable us to combine the nodal information to complete the graph embedding. This treatment lets us extrapolate the finite element solutions in the latent space (see Figure below). While this seems like a curve-fitting in a high-dimensional space, the trick to enhance the physics compatibility of the model is to use the solutions generated from the graph auto-encoder to form another Galerkin projection spanned by a very few potential candidate solutions. In other words, instead of assuming that the GNN predicts the finite element solutions, we only assume that the GNN may prediction something quite close. We then leverage this proximity to sample a few snapshots of the response surface to form a temporary space spanned by those candidate solutions. This allows us to solve the Galerkin projection of the balance principle with just the coefficient of the candidate solutions as unknown. Unlike classical reduced order modeling where a linear embedding is used throughout the entire simulations, our new model may generate different Euclidean space at different locations of the parametric space due to the nonlinear embedding afforded by the GNN. A key benefit of the proposed method is that it does not require searching for the optimal set of parameters in a highly nonlinear landscape (of neural networks). Hence, it does not get stuck in a local minimizer, while it enables the GNN-enabled reduced order simulations to perform with a consistent calculation time. Preprint available at ResearchGate [URL]. This paper is Part III of our quest on introducing geometric learning for a variety of computational mechanics problems. The first two parts can be found below.
PhD student Bahador Bahmani passed the qualification exam and won the Dongju Lee '03 Memorial Award5/26/2023 Our PhD student Bahador Bahmani has passed the qualification exam at Columbia University. His proposed dissertiation "Manifold-embedding data-driven mechanics" focuses on applying manifold learning to enable robust model-free simulations. He has published 6 journal articles, including two papers in CMAME and one in JMPS on the topic of data-driven simulations.
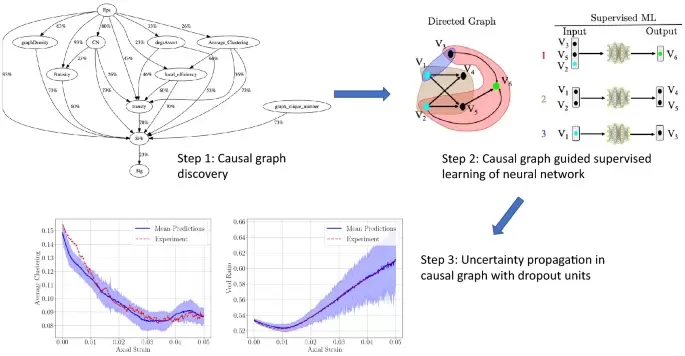
In addition, he has also collaborated in our collaborative NSF project and MURI projects and published papers on causal discovery of granular physics, equviariant geometric learning for digital rock physics, and Generative Adversartial Network for generating microstructures (see below).
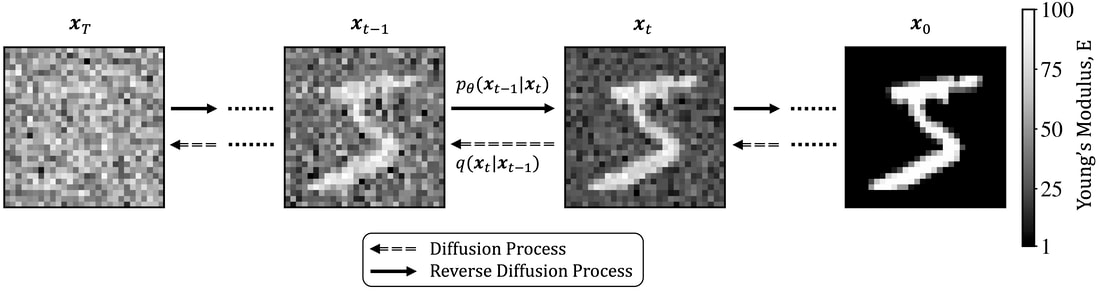
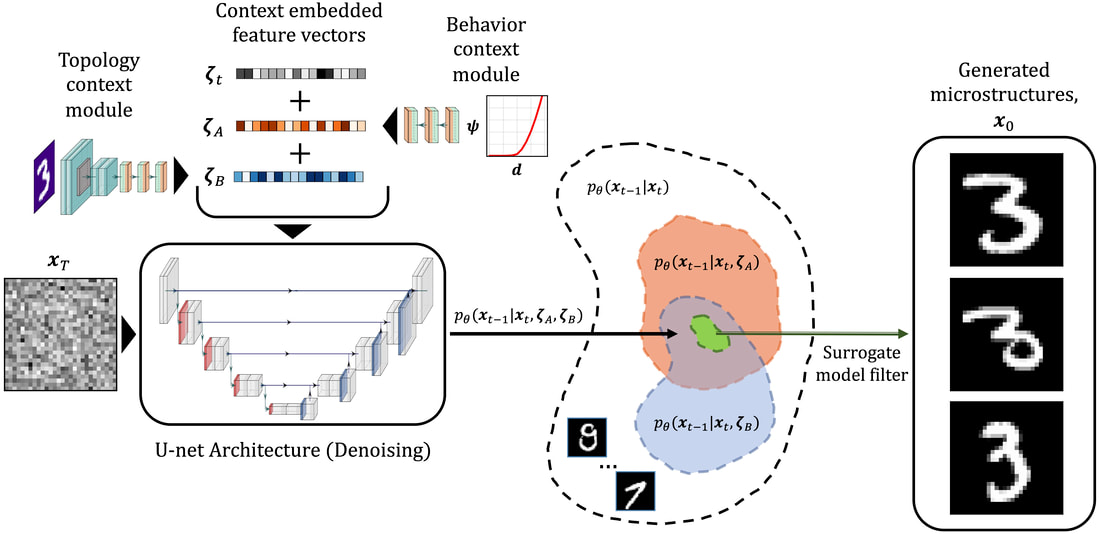
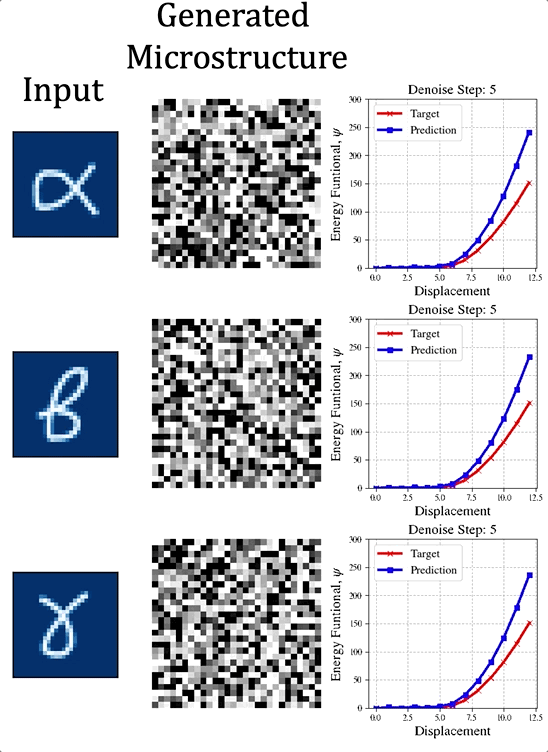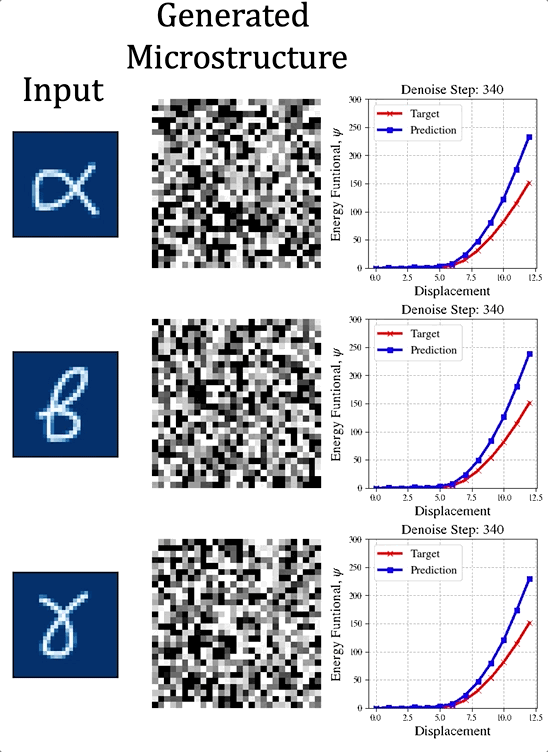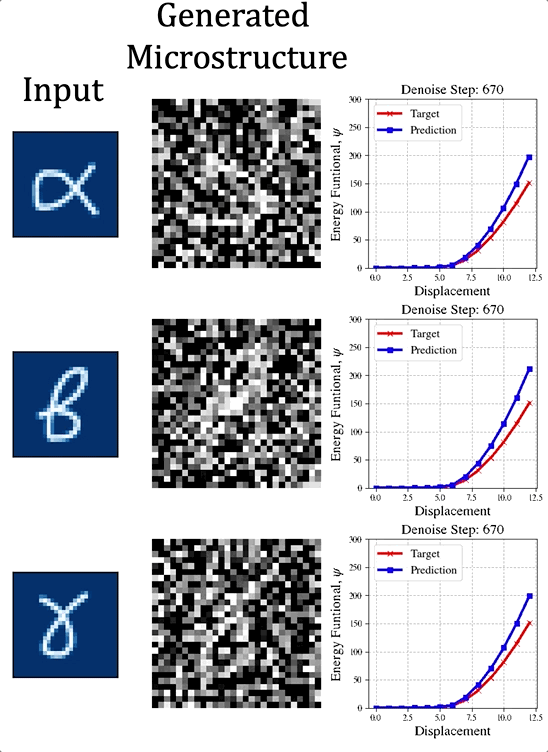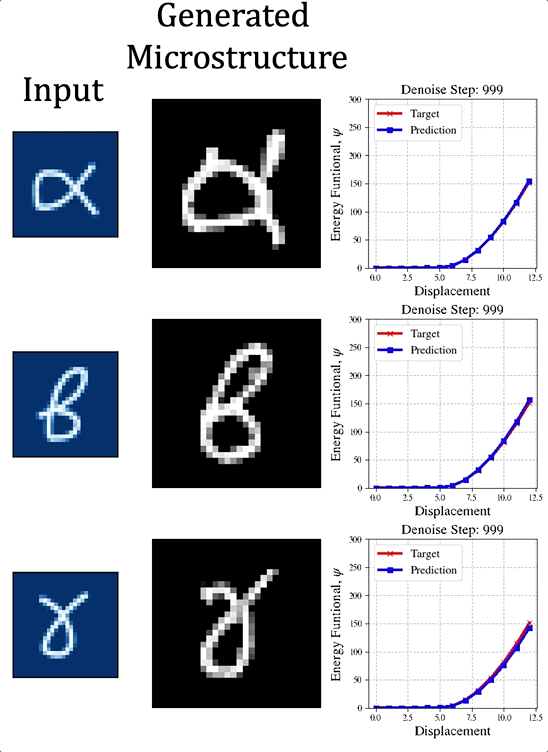
The Dongju Lee memorial award is given in recognition of Bahador's achievement and in honor of his integrity, curiosity and creativity. The Dongju Lee Memorial Award and Memorial Lecture were established with a generous contribution from the Lee Family. Congratulations, Bahador for your outstanding achievement! The paper preprint is available at [URL] In this paper, we (first author = Nick Vlassis) introduce a denoising diffusion algorithm to discover microstructures with nonlinear fine-tuned properties. Denoising diffusion probabilistic models are generative models that use diffusion-based dynamics to gradually denoise images and generate realistic synthetic samples. By learning the reverse of a Markov diffusion process, we design an artificial intelligence to efficiently manipulate the topology of microstructures to generate a massive number of prototypes that exhibit constitutive responses sufficiently close to designated nonlinear constitutive responses. While the unconditional diffusion described in the previous section can readily generate microstructures consistent with the training data set, our goal is to design microstructures that exhibit prescribed mechanical behaviors. To achieve this goal, we use a conditional diffusion process which fine-tunes the resultant microstructures via feature vectors. To identify the subset of micro-cstructures with sufficiently precise fine-tuned properties, a convolution neural network surrogate is trained to replace high-fidelity finite element simulations to filter out prototypes outside the admissible range. Results of this study indicate that the denoising diffusion process is capable of creating microstructures of fine-tuned nonlinear material properties within the latent space of the training data. More importantly, this denoising diffusion algorithm can be easily extended to incorporate additional topological and geometric modifications by introducing high-dimensional structures embedded in the latent space. Numerical experiments is conducted via the open-source mechanical MNIST data set created by Prof. Lejeune research group (See below). Consequently, this algorithm is not only capable of performing inverse design of nonlinear effective media, but also learns the nonlinear structure-property map to quantitatively understand the multi-scale interplays among the geometry, topology, and their effective macroscopic properties.
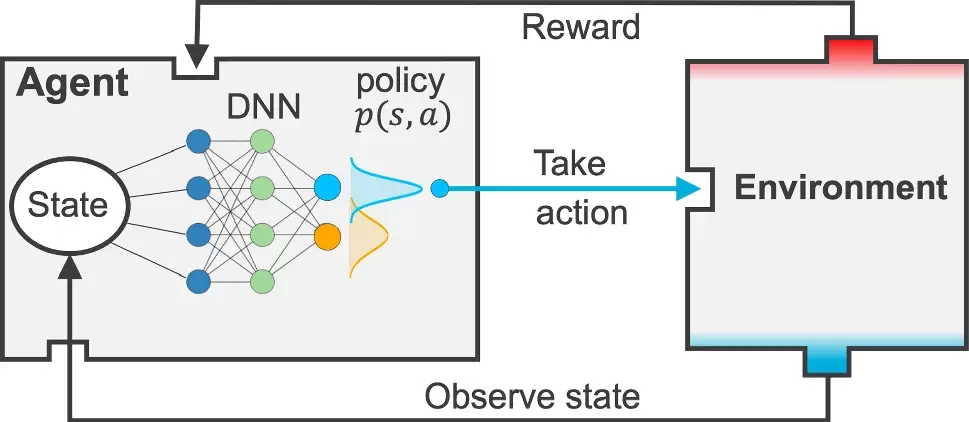
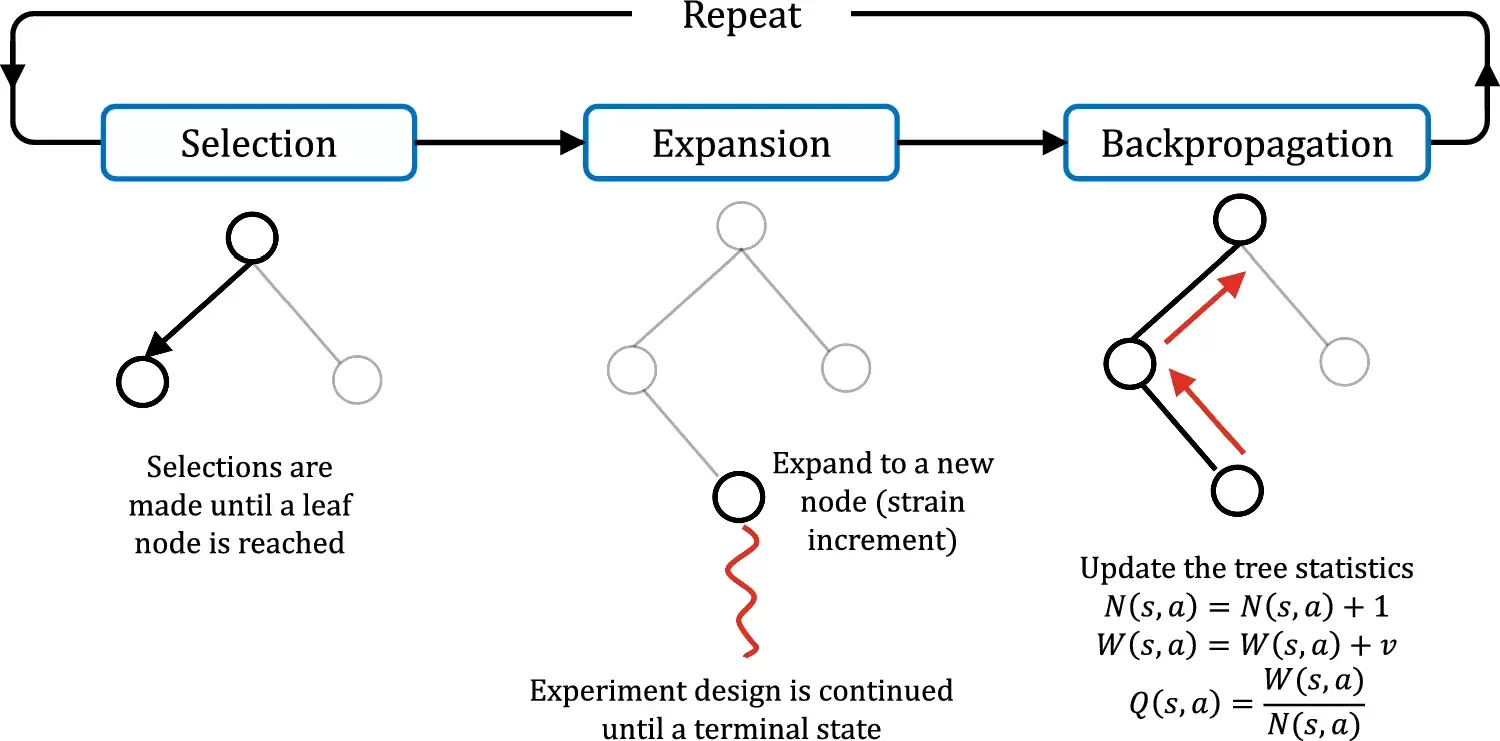
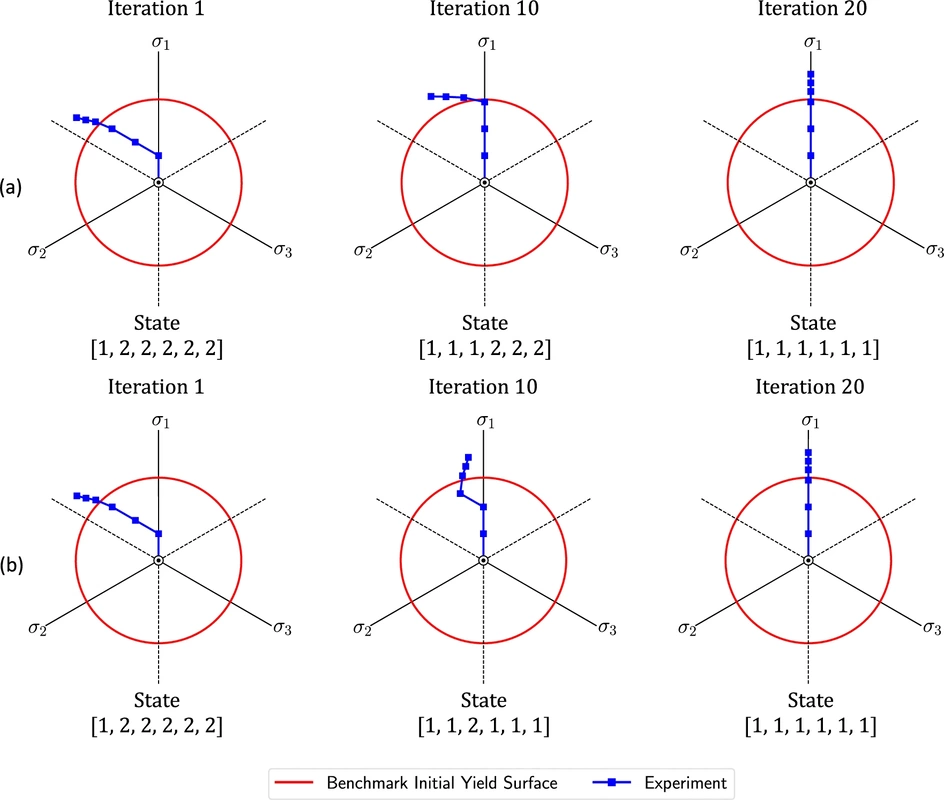
Our collaborative work with Sandia funded by the LDRD project led by Dr. Sharlotte Kramer has just published in the special issue "Machine Learning Theories, Modeling, and Applications to Computational Materials Science, Additive Manufacturing, Mechanics of Materials, Design and Optimization". The article is available in the Computational Mechanics website [URL]. Experimental data are often costly to obtain, which makes it difficult to calibrate complex models. For many models an experimental design that produces the best calibration given a limited experimental budget is not obvious. This paper introduces a deep reinforcement learning (RL) algorithm for design of experiments that maximizes the information gain measured by Kullback–Leibler divergence obtained via the Kalman filter (KF), see figure below. This combination enables experimental design for rapid online experiments where manual trial-and-error is not feasible in the high-dimensional parametric design space. We formulate possible configurations of experiments as a decision tree and a Markov decision process, where a finite choice of actions is available at each incremental step. Once an action is taken, a variety of measurements are used to update the state of the experiment. This new data leads to a Bayesian update of the parameters by the KF, which is used to enhance the state representation. In contrast to the Nash–Sutcliffe efficiency index, which requires additional sampling to test hypotheses for forward predictions, the KF can lower the cost of experiments by directly estimating the values of new data acquired through additional actions. In this work our applications focus on mechanical testing of materials. Numerical experiments with complex, history-dependent models are used to verify the implementation and benchmark the performance of the RL-designed experiments.
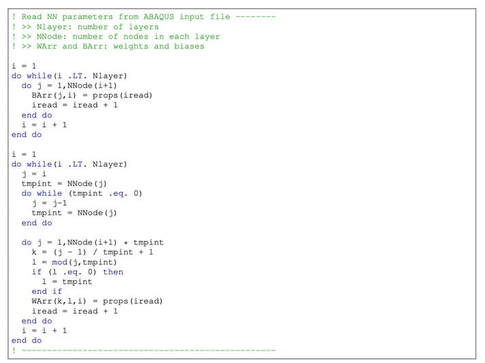 .Our collaborative research with Sandia National Laboratories on pyTorch-UMAT implementation for machine learning models has been accepted by Mechanics of Materials (See preprint [PDF]). This paper introduces a publicly available PyTorch-ABAQUS deep-learning framework of a family of plasticity models where the yield surface is implicitly represented by a scalar-valued function. Our goal is to introduce a practical framework that can be deployed for engineering analysis that employs a user-defined material subroutine (UMAT/VUMAT) for ABAQUS, which is written in FORTRAN (see below) To accomplish this task while leveraging the back-propagation learning algorithm to speed up the neural-network training, we introduce an interface code where the weights and biases of the trained neural networks obtained via the PyTorch library can be automatically converted into a generic FORTRAN code that can be a part of the UMAT/VUMAT algorithm. To enable third-party validation, we purposely make all the data sets, source code used to train the neural-network-based constitutive models, and the trained models available in a public repository. See the link below: https://github.com/hyoungsuksuh/ABAQUS_NN A variety of options (see below) of NN architecture has been pre-trained (see below).. Benchmark material point simulations and finite element simulations in ABAQUS has been provided in the repository. Please feel free to modify the codes and we would appreciate that if you can cite this paper if you use it for your own research. Note: we are actively developing this repository which may contain bugs. If you encounter a bug, please let us (Hyoung Suk Suh, [email protected]; WaiChing Sun, [email protected]) know. Please cite our work if you use it for your own research. We hope that this small tool can encourage and help more researchers from the ABAQUS ecosystem to build their own neural network model. Thank you! Reference:
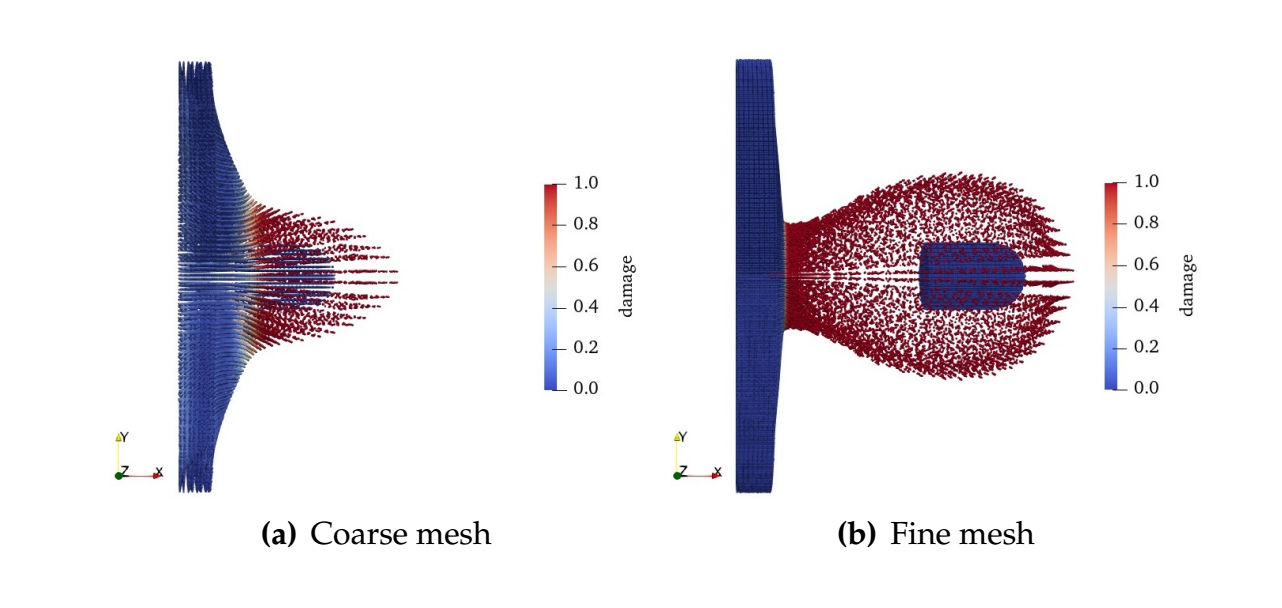
— Steve Sun (@Poromechanics) March 28, 2023
Congratulations again to Nick!
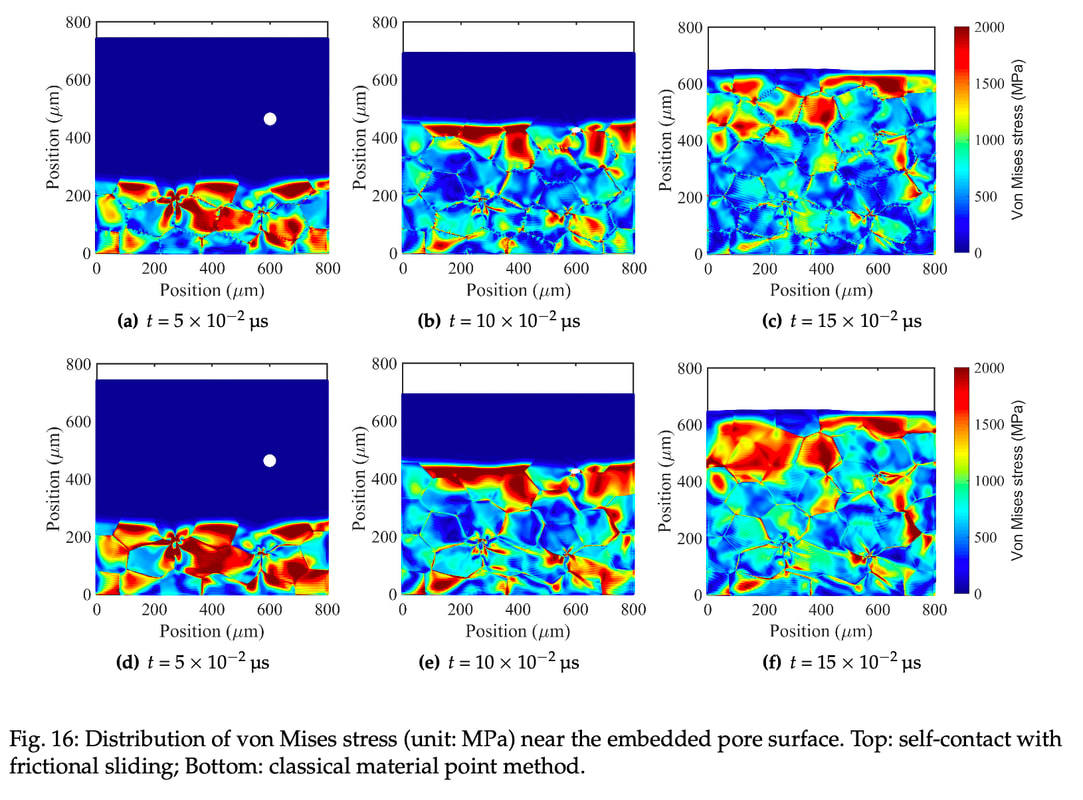
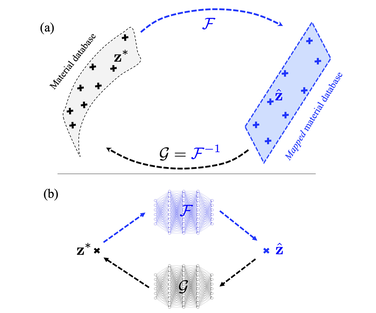
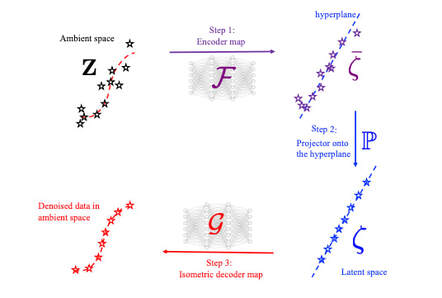 We (first author = Bahador Bahmani) introduce an isometric manifold embedding data-driven paradigm designed to enable model-free simulations with noisy data sampled from a constitutive manifold. The proposed data-driven approach iterates between a global optimization problem that seeks admissible solutions for the balance principle and a local optimization problem that finds the closest point projection of the Euclidean space that isometrically embeds a nonlinear constitutive manifold. To de-noise the database, a geometric autoencoder is introduced such that the encoder first learns to create an approximated embedding that maps the underlying low-dimensional structure of the high-dimensional constitutive manifold onto a flattened manifold. Unlike conventional auto-encoder where the dimension is reduced by reducing the number of neurons in the downstream layers, we reduce the dimension in a geometric sense through the flattening process. We then obtain the noise-free constitutive responses by projecting data onto a de-noised latent space that is completely flat by assuming that the noise and the underlying constitutive signal are orthogonal to each other, leveraging the conformal mapping between the de-noised latent space and the reconstructed de-manifold. Consequently, a projection from the conservative manifold onto this de-noised constitutive latent space enables us to complete the local optimization step of the data-driven paradigm. Our results show that the isometry constraint may prevent the decoder reintroducing noise. Numerical examples are used to both validate the implementation and demonstrate the accuracy, robustness, and limitations of the proposed paradigm. Preprint available [URL]. Authors: Ran Ma, WaiChing Sun, Catalin R. Picu, Tommy Sewell Preprint: [URL] Abstract: Heterogeneous energetic materials (EMs) subjected to mechanical shock loading exhibit complex thermo-mechanical processes which are driven by the high temperature, pressure, and strain rate behind the shock. These lead to spatial energy localization in the microstructure, colloquially known as ``hotspots'', where chemistry may commence possibly culminating in detonation. Shock-induced pore collapse is one of the dominant mechanisms by which localization occurs. In order to physically predict the shock sensitivity of energetic materials under these extreme conditions, we formulate a multiplicative crystal plasticity model with key features inferred from molecular dynamics (MD) simulations. Within the framework of thermodynamics, we incorporate the pressure dependence of both monoclinic elasticity and critical resolved shear stress into the crystal plasticity formulation. Other fundamental mechanisms, such as strain hardening and pressure-dependent melting curves, are all inferred from atomic-scale computations performed across relevant intervals of pressure and temperature. To handle the extremely large deformation and the evolving geometry of the self-contact due to pore collapse, we leverage the capabilities of the Material Point Method (MPM) to track the interface via the Lagrangian motion of material points and the Eulerian residual update to avoid the mesh distortion issue. This combination of features enables us to simulate the shock-induced pore collapse and associated hotspot evolution with a more comprehensive physical underpinning, which we apply to the monoclinic crystal beta-HMX. Treating MD predictions of the pore collapse as ground truth, head-to-head validation comparisons between MD and MPM predictions are made for samples with identical sample geometry and similar boundary conditions, for reverse-ballistic impact speeds ranging from 0.5 to 2km per second. Comparative studies are performed to reveal the importance of incorporating a frictional contact algorithm, pressure-dependent elastic stiffness, and non-Schmid type critical resolved shear stress in the mesoscale model. Case 1: impact velocity = 320 meter per second Case 2: impact velocity = 840 meter per second  Impact simulations for polycrystals
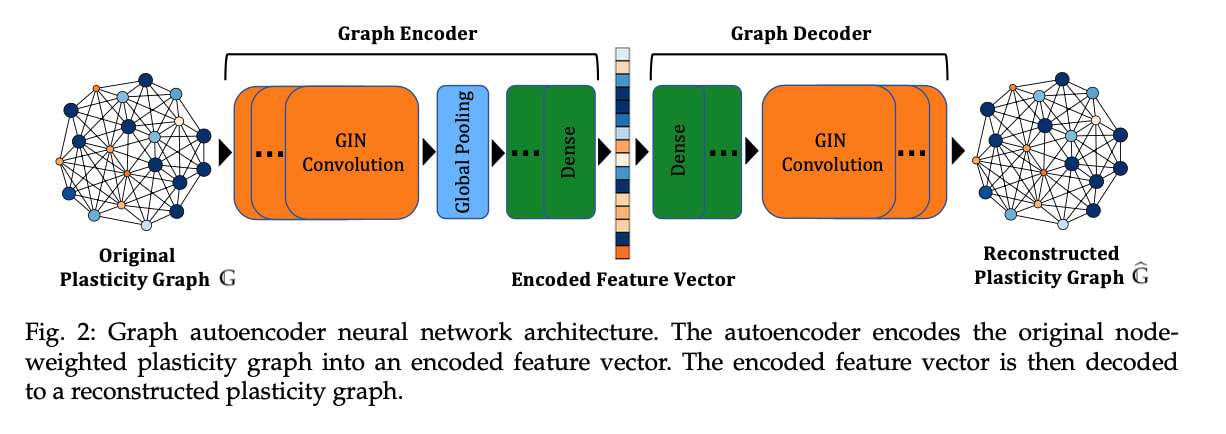
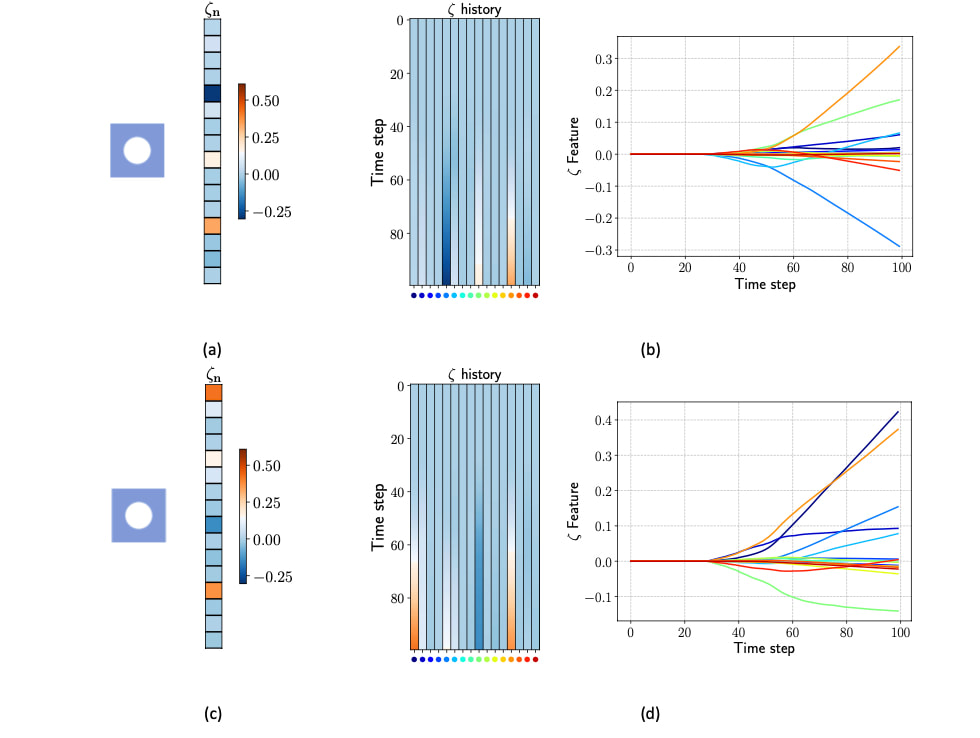
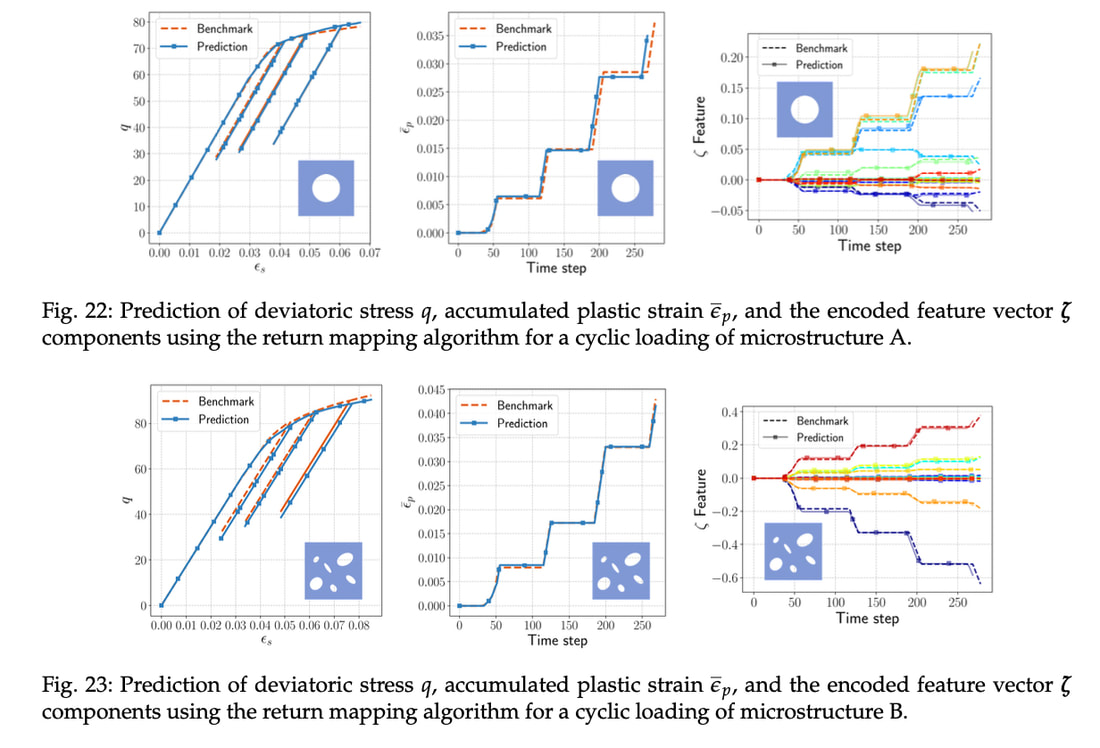
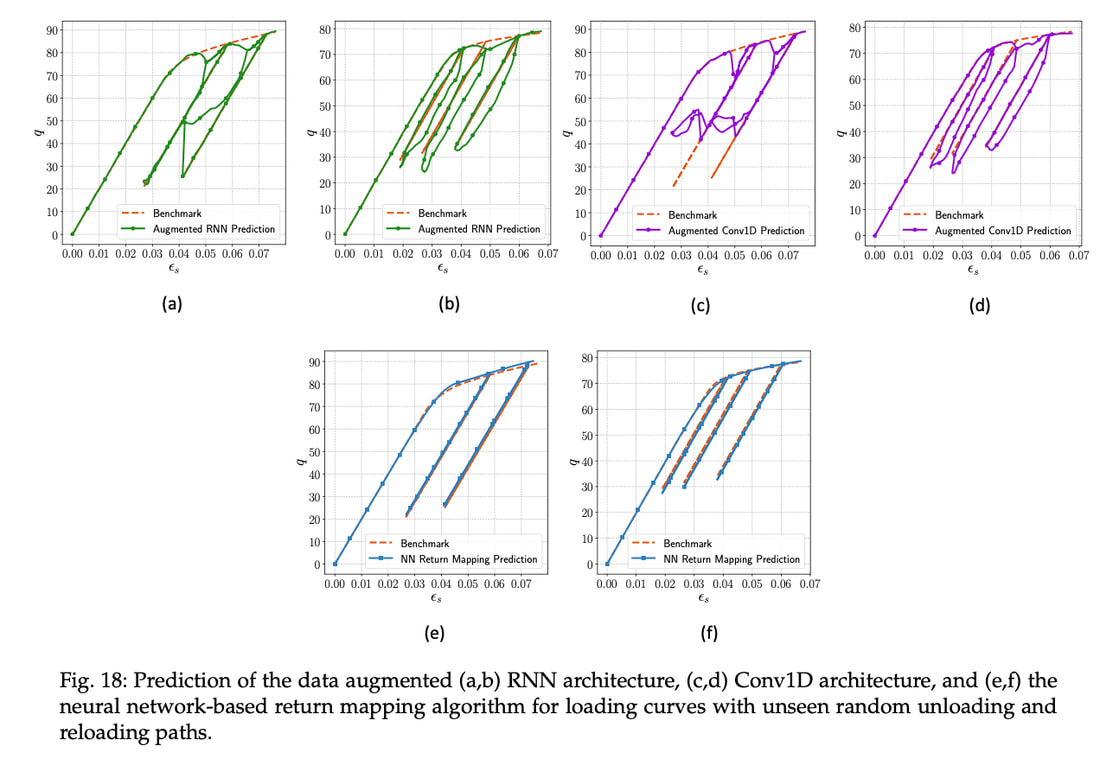
Generally speaking, reduced order modeling and constitutive modeling are considered different disciplines. In Part II of our research on geometric learning for computational Mechanics (see Part I here), we attempt to conduct these two very different ideas by using a graph isomorphism network to learn the low-dimensional representation of finite element solutions of microstructures. Then, instead of reconstructing the low-dimensional dynamics directly via a black-box approach, we use the macroscopic plasticity theory to create additional constraints (e.g., yield function consistency, plastic flow direction) such that the low-dimensional dynamics can be compatible with the macroscopic observations. On the other hand, the autoencoder of the graph isomorphism network also gives us a chance to recast the element of the latent space as the internal variables of the plasticity model and therefore gives more direct and interpretable relations between microstructural deformation patterns and macroscopic plasticity. Our results also indicate that the geometric learning approach may enable us to more explicitly understand the geometry of the data manifested by the shape of the yield function as a function of both stress and elements of latent space of plastic deformation of RVE. This understanding, in return, gives us the opportunity to recast the reduced order modeling problem that can be updated via a classical constitutive law that is now with internal variables that can b be encoded as a snapshot of finite element mesh. The resultant models is found to perform robustly in forward predictions with loading paths different from the training data, in thew sense that there is no spurious patterns that might exhibit in RNN or 1D convolutional NN (see below).
Preprint posted at ResearchGate here. Part III of this series is under progress and will submit soon. In this work, we first use MD data to train a deep neural network to create the "first draft" of the continuum surrogate model, then use well known physics constraints from continuum mechanics (e.g. material frame indifference, material symmetry, growth condition, rank-one convexity) to further fine-tune the neural network. The resultant framework is used to predict the finite strain elasticity of Nitroamine high explosive (HMX), an application that requires robustness and consistency on the forecast quality.
Link to research article: https://onlinelibrary.wiley.com/doi/10.1002/nme.6992 Link to the cover: https://onlinelibrary.wiley.com/doi/epdf/10.1002/nme.7087 Link to research article: onlinelibrary.wiley.com/doi/10.1002/nag.3408
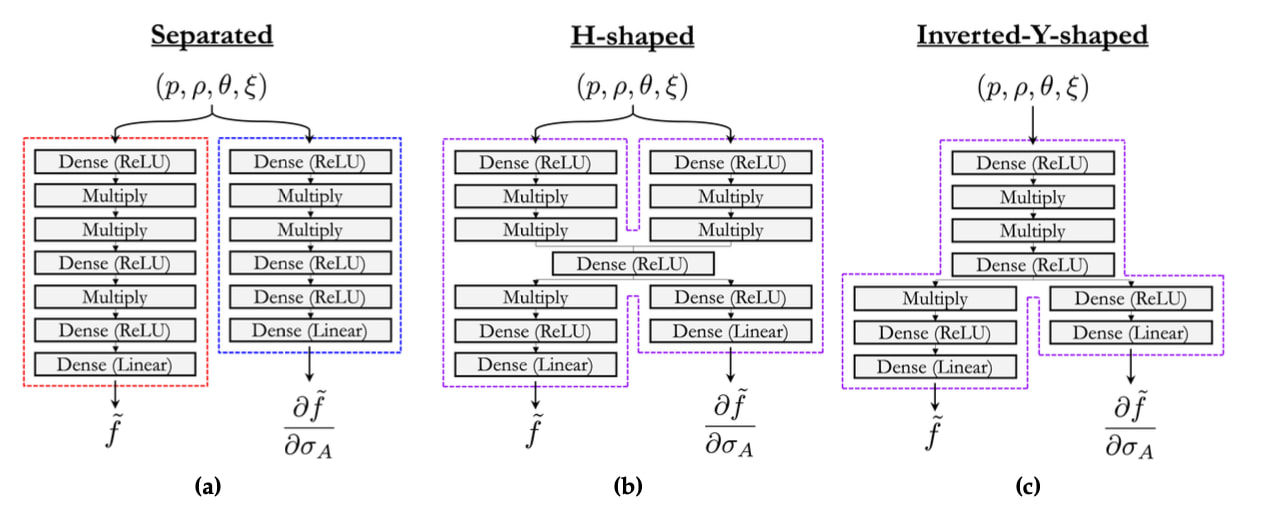
Link to the cover: https://onlinelibrary.wiley.com/doi/epdf/10.1002/nag.3437 When predicting plastic responses of complex microstructures, we often propose mechanisms to explain the physics of the yielding, then propose mathematical expressions to recapture what we describe in words, then propose algorithms to generate the constitutive updates. However, what if the materials are so complex that we cannot easily find a single equation to express them precisely? What if our symbolic regression skill is not sufficient to recover the surface to which those data points belong? The yield function or damage criterion of a material is a common example where our abilities to compose equations precisely and accurately are often put to test. A yield function may take many different types of variables (stress invariants, strain, sometimes also other descriptors such as volume fraction). A simple solution we proposed is to not propose the yield surface as a function in the parametric space but directly regard it as a manifold. In this work (first author = Mian Xiao), Mian and I explore the use of geometric prior to generating the yielding manifold based on point cloud data obtained from direct numerical simulations or experiments. By modifying the geometric approach by Williams, et al. CVPR 2019 to incorporate plastic flow information to regularize the yield surface, we have successfully recovered a highly complex yield surface through the construction of a collection of coordinate charts and the atlas, a task that is difficult to complete via training a single neural network. Meanwhile, we also show that the availability of local patches also enables us to overcome the longstanding slow convergence issue commonly exhibited in classical non-smooth plasticity models and leads to a very robust reconstruction of yield surface even with noisy data. Preprint available via ResearchGate. [PDF] Link to open-access article: https://onlinelibrary.wiley.com/doi/full/10.1002/nag.3380
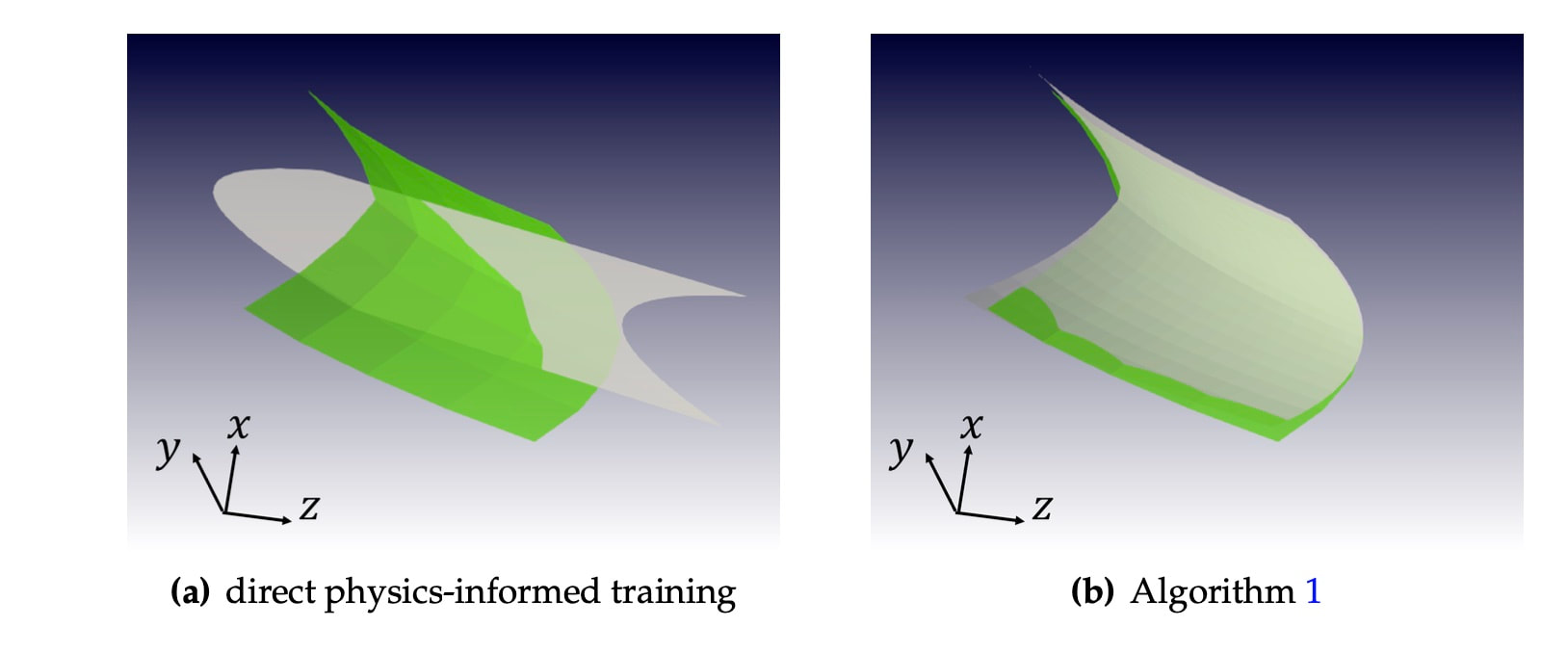
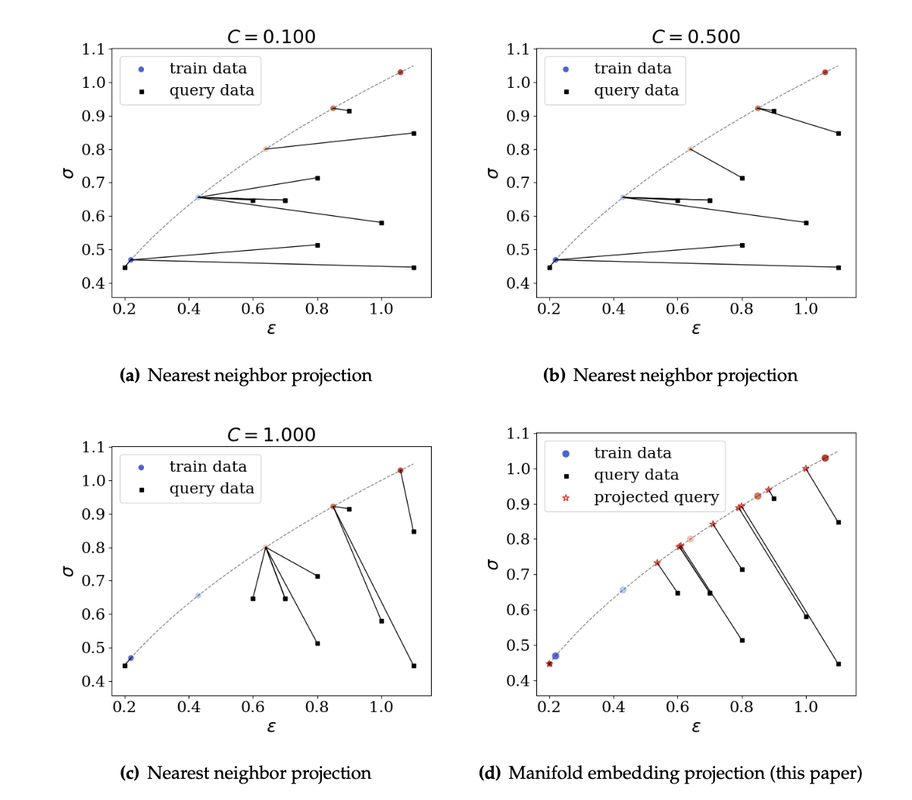
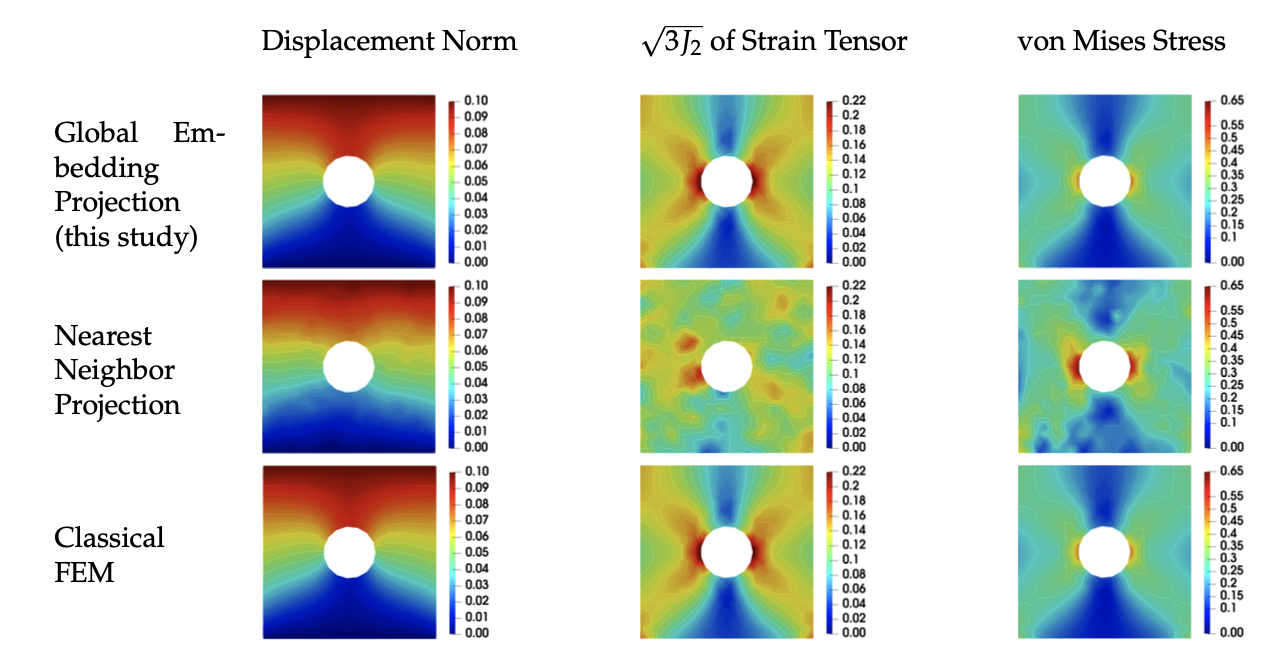
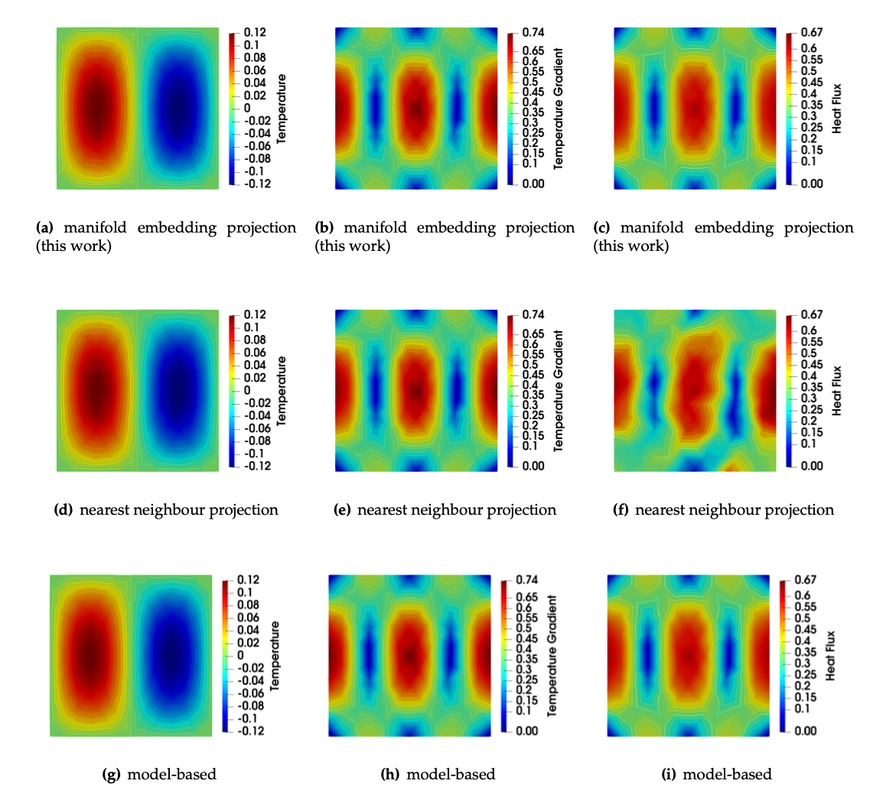
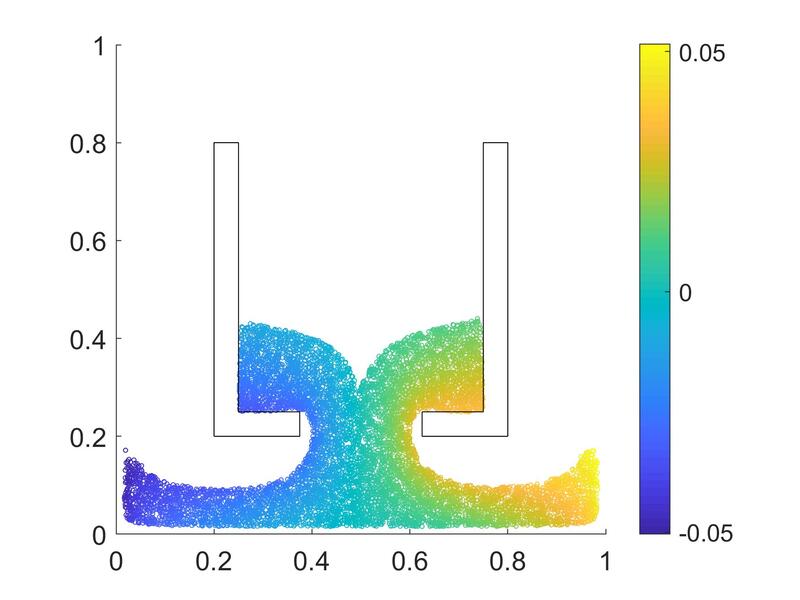
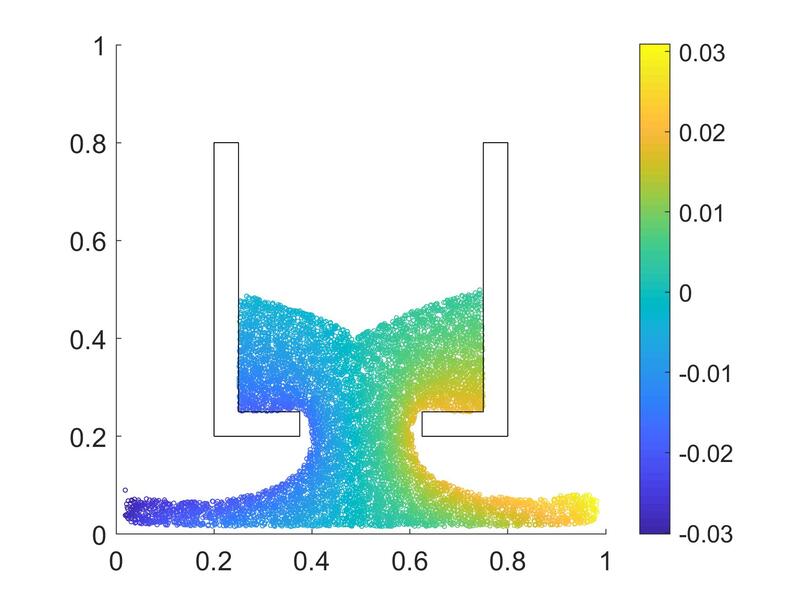
Link to the cover: https://onlinelibrary.wiley.com/doi/10.1002/nag.3429 This article (see [preprint]) presents a multi-phase-field poromechanics model that simulates the growth and thaw of ice lenses and the resultant frozen heave and thaw settlement in multi-constituent frozen soils. In this model, the growth of segregated ice inside the freezing-induced fracture is implicitly represented by the evolution of two phase fields that indicate the locations of segregated ice and the damaged zone, respectively. The evolution of two phase fields is induced by their own driving forces that capture the physical mechanisms of ice and crack growths respectively, while the phase field governing equations are coupled with the balance laws such that the coupling among heat transfer, solid deformation, fluid diffusion, crack growth, and phase transition can be observed numerically. Unlike phenomenological approaches that indirectly capture the freezing influence on the shear strength, the multi-phase-field model introduces an immersed approach where both the homogeneous freezing and the ice lens growth are distinctively captured by the freezing characteristic function and the driving force accordingly. Verification and validation examples are provided to demonstrate the capacities of the proposed models. Support provided by US Army Research Office and National Science Foundation is gratefully acknowledged. The first author of this paper, the 6th graduated PhD of our group, Dr. Hyoung Suk Suh (see picture below) has received the DongJu Lee '03 Memorial Award in recognition of "his superior achievement and in honor of the integrity, curiosity, and creativity exhibited as a student at SEAS of Columbia." Congratulations, Hyoung Suk! I am looking forward for more great news in the upcoming year! This paper (see the preprint available here) introduces a manifold embedding data-driven paradigm to solve small- and finite-strain elasticity problems without a conventional constitutive law. 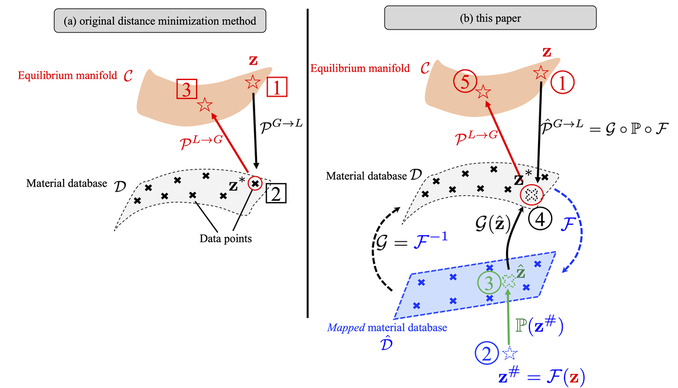 Traditionally, data-driven paradigm often replace a constitutive law with a search that select an experimental data point that is " the closest" to the balance principle. However, how distance or length is measured remains ambiguous. Often time, an arbitrarily energy norm is chosen, but such a practice has shown to be affected which closest data point is getting selected. In particular, in a nonlinear manifold, the shortest distance between two points and the Euclidean distance can be quite different when they are far apart. Furthermore, the resultant model-free simulation could be sensitive to the chosen norm used to measure distance (see figure below). We follows the classical data-driven paradigm by seeking the solution that obeys the balance of linear momentum and compatibility conditions while remaining consistent with the material data through minimizing a distance measure. Our key point of departure is the introduction of a global manifold embedding as a means to learn the geometrical trend of the constitutive data mathematically represented by a smooth manifold. Conventionally, an incremental nonlinear constitutive update is sought by solving a sequence of linearized equations that moves along the admissible range of the constitutive law until the solution is found. Instead of doing this, we propose to simply deform the phase space where the nonlinear constitutive law exists such that the resultant constitutive law in the deformed space appear to be linear. A pair of neural networks (see below) are trained to learn (1) how to deform this nonlinear constitutive manifold to make it flat (i.e. there is one normal vector everywhere in the deformed hyperplane), and (2) how to deform the hyperplane back into a smooth manifold. Consequently, the flatness of the deformed hyperplane then makes it very easy to measure the distance between a point and the hyperplane, while the inverse map allows us to convert the local search result back into a point in the nonlinear constitutive law. By training an invertible neural network to embed the data of an underlying constitutive manifold onto a Euclidean space, we reformulate the local distance-minimization problem such that it replace the computationally intensive combinatorial search to identify the optimal data points closest to the conservation law with a cost-efficient projection step.
Meanwhile, numerical experiments performed on path-independent elastic materials of different material symmetries suggest that the geometrical inductive bias learned by the neural network is helpful to ensure more consistent predictions when dealing with data sets of limited sizes or those with missing data (see examples below). Our paper on capturing evolving anisotropy of freezing clayey soil has been accepted by IJNAMG4/26/2022 Authors: Qing Yin, Edward Andò, Gioacchino Viggiani, WaiChing Sun Abstract: This paper presents a combined experimental-modeling effort to interpret the coupled thermo-hydro-mechanical behaviors of the freezing soil, where an unconfined, fully saturated clay is frozen due to a temperature gradient. By leveraging the rich experimental data from the microCT images and the measurements taken during the freezing process, we examine not only how the growth of ice induces volumetric changes of the soil in the fully saturated specimen but also how the presence and propagation of the freezing fringe front may evolve the anisotropy of the effective media of the soil-ice mixture that cannot be otherwise captured phenomenologically in the isotropic saturation-dependent critical state models for plasticity. The resultant model is not only helpful for providing a qualitative description of how freezing affects the volumetric responses of the clayey material, but also provide a mean to generate more precise predictions for the heaving due to the freezing of the ground. [PDF]  Congratulations to Dr. Hyoung Suk Suh for successfully defending his PhD dissertation (see URL). We are very grateful to other committee members, Professor Ronaldo Borja, Professor George Deodatis, Professor Majid Manzari and Professor Haim Waisman for their suggestions and feedbacks, and the Army Research Office and National Science Foundation for providing the financial support for his PhD study. Hyoung Suk joined my research group in 2018 from Yonsei University. He has published the following works during his tenure at Columbia. His PhD work focuses on the microporomechanics of geomaterials at extreme temperature with implications on how climate changes may affect the freeze-thaw action in frozen soil in Alaska. In addition to his research accomplishment, Hyoung Suk is also a beloved TA and had also been nominated as the candidate for the Presidential awards for outstanding teaching at Columbia twice. Dr. Suh, thank you for the 4 years of hard work and dedications! It is a privilege to serve as your PhD advisor and colleague! Published work:
After 2 years of delay due to pandemic, we are back to the roads now for conferences. Below are two talks, one on phase field modeling of ice lens, one on immersed phase field for fluid-driven fracture with Darcy-Stokes flow. Talk 1: Multi-phase-field approach for modeling ice lens growth and thaw in frozen soil Talk 2: An immersed phase field fracture model in fluid-infiltrating porous media with evolving Beavers-Joseph-Saffman condition  Congratulations to Dr. Kun Wang who has been selected from around 200 applicants by ExxonMobil! He will join Computational Physics Section at EMRE’s Corporate Strategic Research Laboratories as a computational physicist to develop computational methods aimed at solving large-scale physical problems pertaining to the energy industry, with focus in the areas of flow in porous media, multi-scale phenomena, PDE-constrained optimization and uncertainty quantification. Kun has a distinguished career at both Columbia University and Los Alamos National Laboratory. His recent work published in Nature Communication and PNAS has been featured at Economist. During his time at Columbia, he has published 12 papers with the research group, as listed below. Published Work:
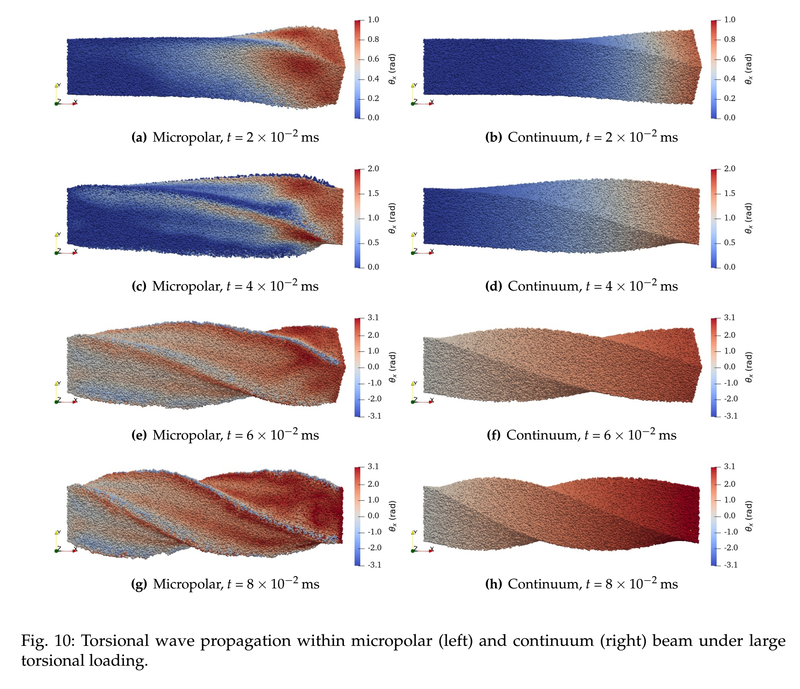
While there are many neural network constitutive laws published, there are relatively little work on focusing on the validation against the physical constraints to make the predictions admissible. In this work, we train the neural network with multiple steps where it first fits the data, then corrections are made through transfer learning to introduce additional physical constraints, such as material frame indifference, material symmetry, as well as checking the ellipticity, growth conditions, stability and uniqueness (through examining the acoustic tensor). Another interesting point is that we are using the gradient and the Hessian data to back calculate the underlying scalar elasticity functional. The neural network model is used to predict the responses of a monoclinic organic molecular crystal, beta-HMX inferred from MD simulations. Accuracy of the blind predictions are tested in the parametric space. Preprint manuscript available at [URL]. Ran Ma and I have our latest work on finite deformation/microrotation MPM for micropolar materials accepted by CMAME before the winter break. There is a great body of work which proves that material point method (MPM) is a great tool to simulate extremely large deformation (even for Lagrangian granular flow). The potential of MPM to handle simulations with large rotation (metal forming, torsional wave...etc) and large micro-rotation for micropolar materials (e.g. sand, meta-materials), is less explored. In this work, we introduce a numerical framework that includes the necessary ingredients, include the explicit time integrator, the Lie-group projections between grid and material points, and a micropolar frictional models for the contact mechanics. Consequentially, the model enables us to introduce a unified approach to simulate dynamic responses of both solid and fluids that exhibit size effects.
To the best of our knowledge, this is the first research successfully enable the simulations of micropolar continuua in MPM in the geometrical nonlinear regime. Preprint available [URL] |
Group NewsNews about Computational Poromechanics lab at Columbia University. Categories
All
Archives
July 2023
|











 RSS Feed
RSS Feed