Our paper with Prof. Vlassis on denoising-diffusion generative model for microstructure design with fined-tuned nonlinear properties has been accepted by CMAME.

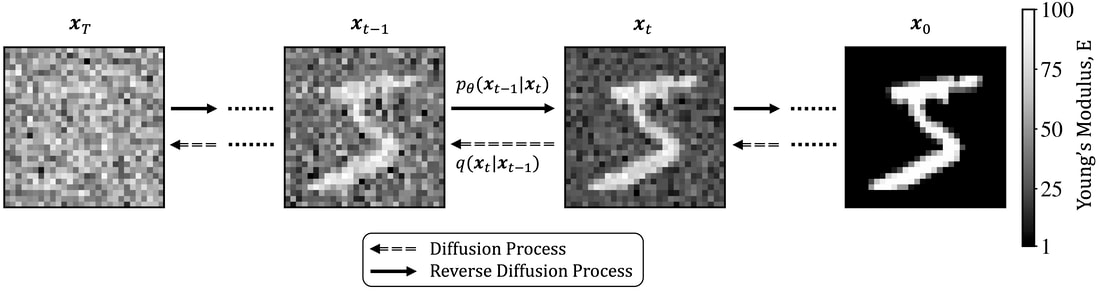
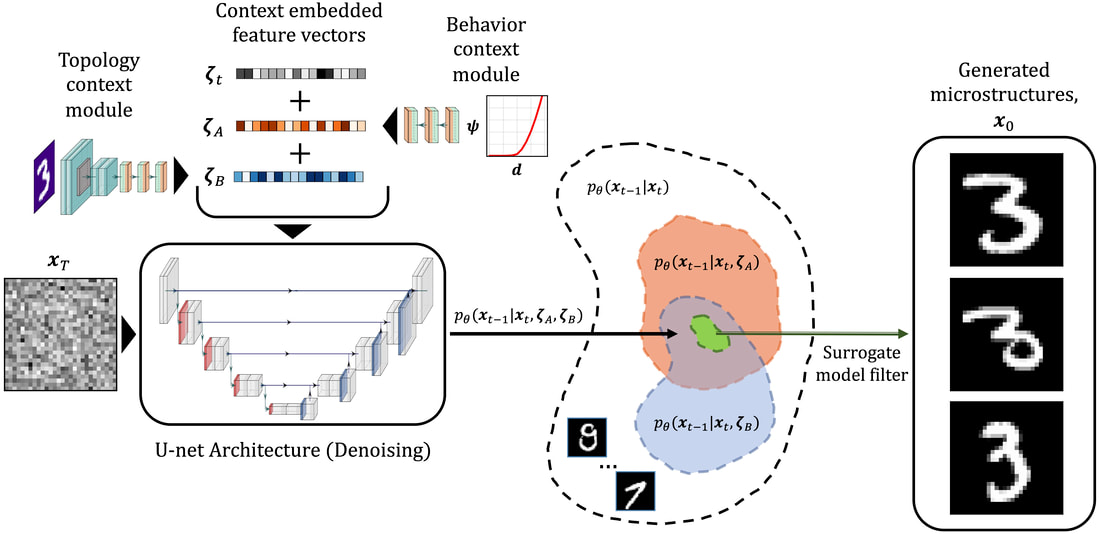
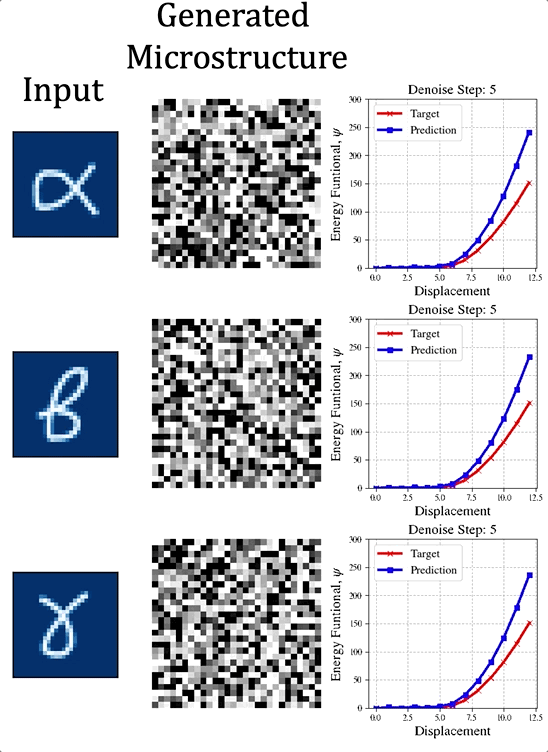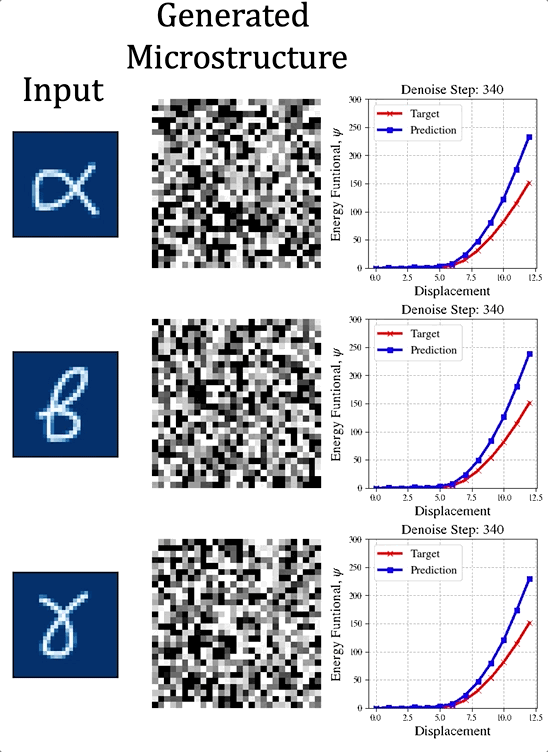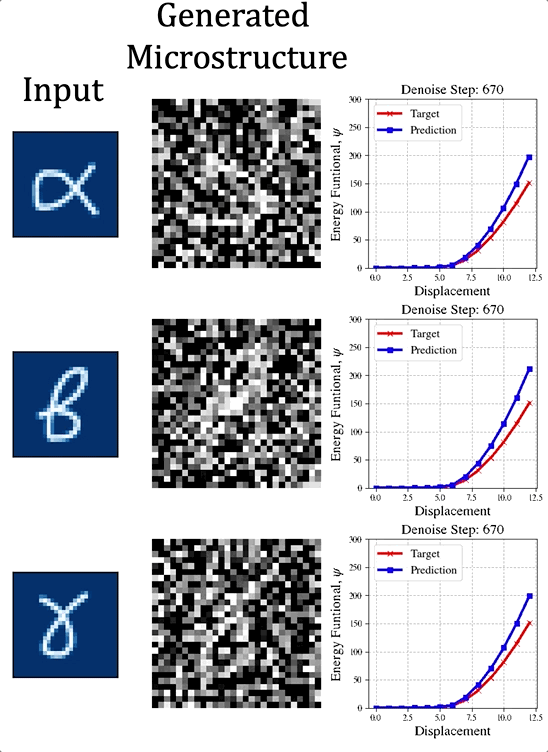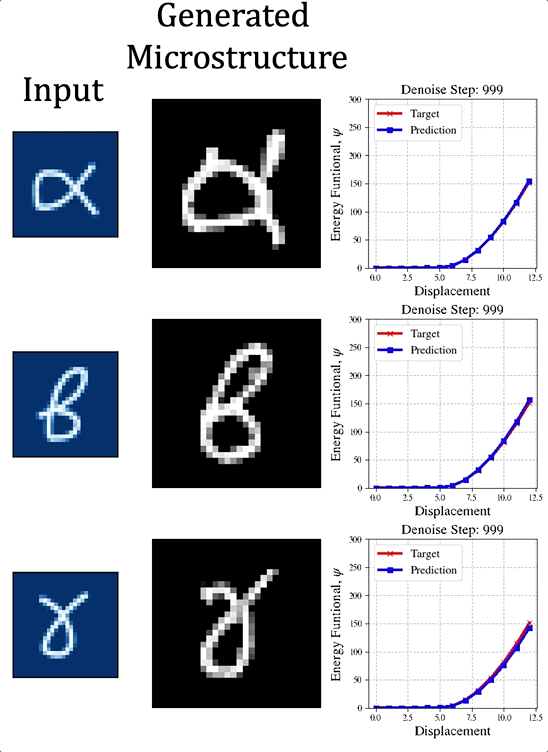
The paper preprint is available at [URL] In this paper, we (first author = Nick Vlassis) introduce a denoising diffusion algorithm to discover microstructures with nonlinear fine-tuned properties. Denoising diffusion probabilistic models are generative models that use diffusion-based dynamics to gradually denoise images and generate realistic synthetic samples. By learning the reverse of a Markov diffusion process, we design an artificial intelligence to efficiently manipulate the topology of microstructures to generate a massive number of prototypes that exhibit constitutive responses sufficiently close to designated nonlinear constitutive responses.

While the unconditional diffusion described in the previous section can readily generate microstructures consistent with the training data set, our goal is to design microstructures that exhibit prescribed mechanical behaviors. To achieve this goal, we use a conditional diffusion process which fine-tunes the resultant microstructures via feature vectors.

To identify the subset of micro-cstructures with sufficiently precise fine-tuned properties, a convolution neural network surrogate is trained to replace high-fidelity finite element simulations to filter out prototypes outside the admissible range. Results of this study indicate that the denoising diffusion process is capable of creating microstructures of fine-tuned nonlinear material properties within the latent space of the training data. More importantly, this denoising diffusion algorithm can be easily extended to incorporate additional topological and geometric modifications by introducing high-dimensional structures embedded in the latent space. Numerical experiments is conducted via the open-source mechanical MNIST data set created by Prof. Lejeune research group (See below). Consequently, this algorithm is not only capable of performing inverse design of nonlinear effective media, but also learns the nonlinear structure-property map to quantitatively understand the multi-scale interplays among the geometry, topology, and their effective macroscopic properties.