|
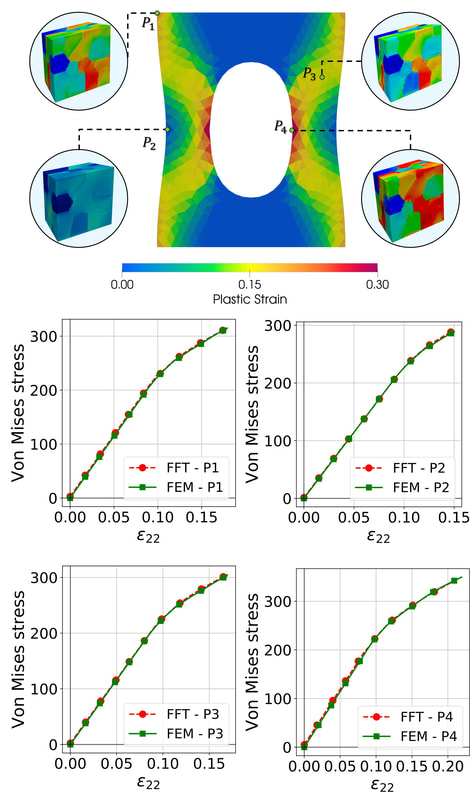
Conventionally, neural network constitutive laws for path-dependent elasto-plastic solids are trained via supervised learning performed on recurrent neural networks, with the time history of strain as input and the stress as input. However, training neural networks to replicate path-dependent constitutive responses requires significantly more data due to the path dependence. This demand on diversity and abundance of accurate data, as well as the lack of interpretability to guide the data generation process, could become major roadblocks for engineering applications. In this work, we attempt to simplify these training processes and improve the interpretability of the trained models by breaking down the training of material models into multiple supervised machine learning programs for elasticity, initial yielding and hardening laws that can be conducted sequentially. To predict pressure-sensitivity and rate dependence of the plastic responses, we reformulate the Hamliton-Jacobi equation such that the yield function is parametrized in a product space spanned by the principal stress, the accumulated plastic strain and time. To test the versatility of the neural network meta-modeling framework, we conduct multiple numerical experiments where neural networks are trained and validated against (1) data generated from known benchmark models (2) data obtained from physical experiments and (3) data inferred from homogenizing sub-scale direct numerical simulations of microstructures. The neural network model is also incorporated into an offline FFT-FEM model to improve the efficiency of the multiscale calculations. Preprint available here [URL]
If the injected fluid is much hotter or colder than the host matrix of the porous media and the specific heat capacities of the solid and fluid constituents are sufficiently different, then the assumption that the two constituents will have the same temperature at the continuum scale may not be correct. In this work, we formulate a dual-heat-transfer theory (in analog to the dual-permeability poromehanics theory) to examine how these local temperature difference affect the fracture patterns and the path-dependent responses at the small time scale and under what condition the one temperature theory is sufficient. To address the issue of the time scale difference of the coupled heat transfer problem, we introduce an asynchronous time integrator for the operator-split algorithm to improve the efficiency of the solver. Preprint available here [URL].  I am excited that the thesis committee (Professor George Deodatis, Professor JS Chen, Professor Richard Regueiro, Professor Marco Giometto and myself) have approved our team member Nick Vlassis's PhD dissertation "Towards Trustworthy Geometric Deep Learning for Elastoplasticity". Nick will continue to collaborate with us on the DOE NNSA project "Center for Micromorphic Multiphysics Porous and Particulate Materials Simulations with Exascale Computing Workflows (MSC)" (by led University of Colorado Boulder) as a Postdoctoral Research Scientist . Nick's work focuses on formulating geometric learning tasks to create meta-models that generate interpretable constitutive laws from MD, DNF, DEM and experimental data across different length scales, often with physical constraints that often involves higher-order derivatives (see list of publication below). During PhD study, Nick has been awarded the Mindlin Scholarship by the Fu Foundation School of Engineering and Applied Science and a few NSF travel fellowships to conferences. Congratulations for the well-deserved distinction, Nick! We are looking forward for your outstanding contribution to the DOE NNSA project! Publications:
In this work, we simulate the fragmentation process of particles by extending the domain partition MPM first introduced by Homel and Herbold 2017 to analyze how the thermal-coupling and surface-conductance affect the contact/fracture mechanics of granular materials. This framework enables us to circumvent the unrealistic crack patterns caused by using the homogenized stress of each particle as a criterion for fragmentation or straight split while capturing the strain-rate sensitivity of the fragmentation process simply through simulating crack branching. Abstract: We propose a material point method (MPM) to model the evolving multi-body contacts due to crack growth and fragmentation of thermo-elastic bodies. By representing particle interface with an implicit function, we adopt the gradient partition techniques introduced by Homel and Herbold 2017 to identify the separation between a pair of distinct material surfaces. This treatment allows us to replicate the frictional heating of the evolving interfaces and predict the energy dissipation more precisely in the fragmentation process. By storing the temperature at material points, the resultant MPM model captures the thermal advection-diffusion in a Lagrangian frame during the fragmentation, which in return affects the structural heating and dissipation across the frictional interfaces. The resultant model is capable of replicating the crack growth and fragmentation without requiring dynamic adaptation of data structures or insertion of interface elements. A staggered algorithm is adopted to integrate the displacement and temperature sequentially. Numerical experiments are employed to validate the diffusion between the thermal contact, the multi-body contact interactions and demonstrate how these thermo-mechanical processes affect the path-dependent behaviors of the multi-body systems. Preprint: Available via ResearchGate: [URL] Video Summary: https://youtu.be/pg535F6bqtQ Starting next month, the PI of Sun Group will join the editorial board of Acta Geotechnica:
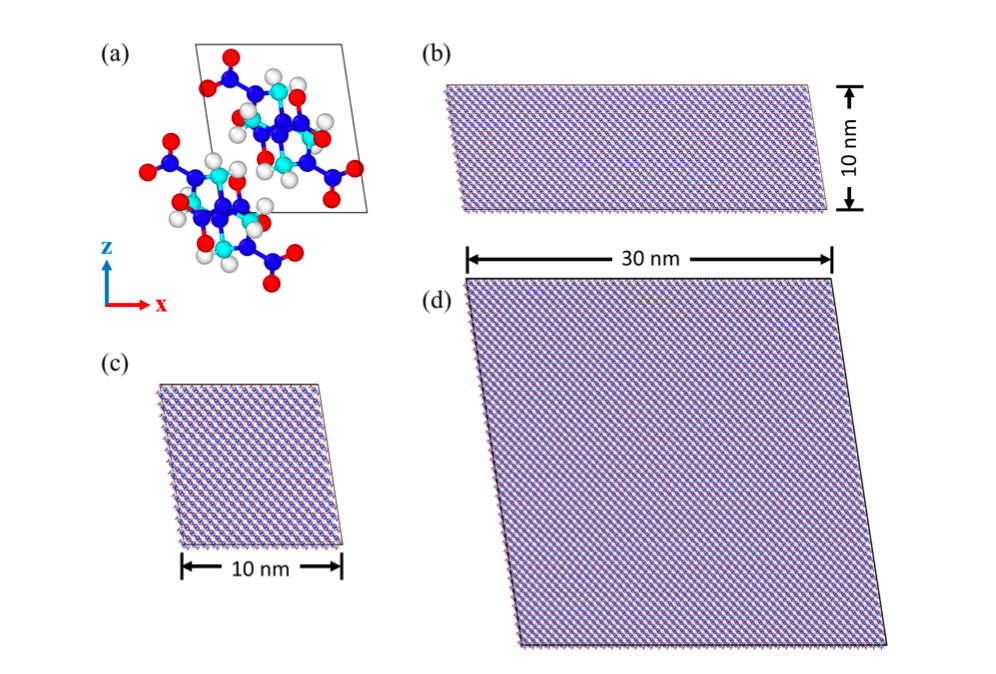
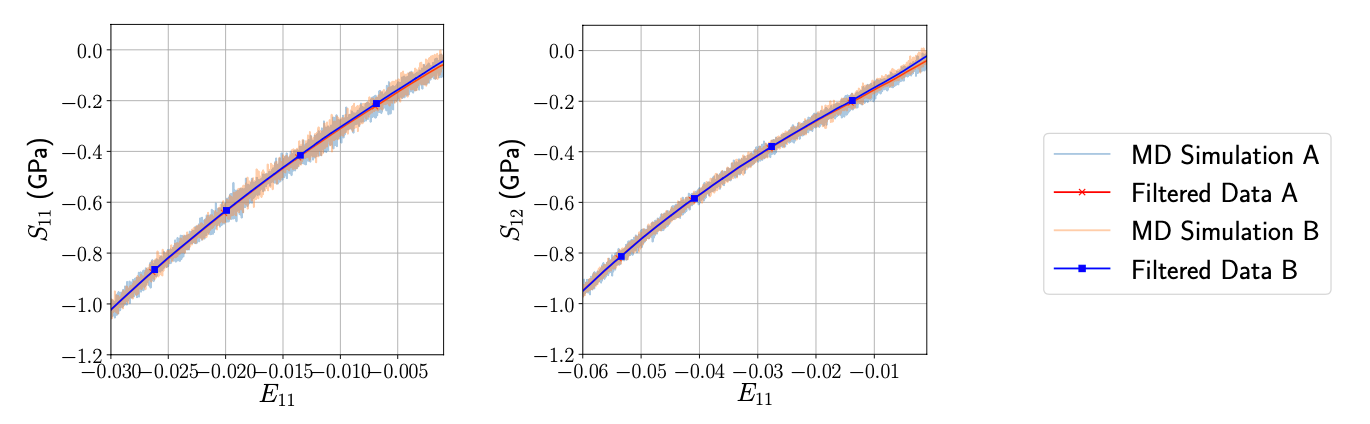
https://www.springer.com/journal/11440/editors Author: Xiao Sun, Bahador Bahmani, Nikolaos N. Vlassis, WaiChing Sun, Yanxun Xu Abstract: This paper presents a computational framework that generates ensemble predictive mechanics models with uncertainty quantification (UQ). We first develop a causal discovery algorithm to infer causal relations among time-history data measured during each representative volume element (RVE) simulation through a directed acyclic graph (DAG). With multiple plausible sets of causal relationships estimated from multiple RVE simulations, the predictions are propagated in the derived causal graph while using a deep neural network equipped with dropout layers as a Bayesian approximation for uncertainty quantification. We select two representative numerical examples (traction-separation laws for frictional interfaces, elastoplasticity models for granular assembles) to examine the accuracy and robustness of the proposed causal discovery method for the common material law predictions in civil engineering applications. The preprint is available at [URL]. The key ideas are to explore if causal discovery algorithm can deduce the plausible causal relations and whether the discovered causal relations match with our current state-of-the-art knowledge discovered by human. One interesting aspect I found quite interesting is that, while incorporating the causal relation into the deep learning constitutive laws might improve the interpretability, it does not always improve the accuracy (for instance, when prediction the properties of the immediate vertices is harder than that of the leaves of the causal graph). Abstract: Cyclotetramethylene-Tetranitramine (HMX) is a secondary explosive used in military and civilian applications. Its plastic deformation is of importance in the initiation of the decomposition reaction, but the details of plasticity are not yet fully understood. It has been recently shown that both the elastic constants and the critical resolved shear stress for plastic deformation are pressure sensitive. Since initiation takes place during shock loading, the pressure sensitivity of plasticity is highly relevant. In this work, we examine the pressure-sensitivity of the dynamic mechanical behavior of HMX. To this end, we use an elastic-plastic continuum constitutive model of single crystal HMX in which the anisotropic elastic constants and direction-dependent yield stress are rendered pressure-sensitive. The pressure sensitivity is calibrated based on input from molecular models. We observe that accounting for pressure sensitivity changes significantly the profile of the elastic-plastic wave and the wave propagation speed upon impact. The accumulated dissipation profile and the total dissipation also exhibit profound differences between the simulations that take account of the pressure-dependence of the plastic deformation and the pressure independent counterpart. Preprint: [PDF] 1. An immersed phase field model for fracture-induced Darcy-Stokes flow (presented by PhD student Hyoung Suk Suh). Invited paper published in Physics of Fluid [URL] 2. An accelerated model-free poroelasticity solver with multifidelity multiphysics data (presented by PhD student Bahador Bahmani). Paper accepted by CMAME [URL] 3. AI-generated interpretable plasticity theory (presented by PhD student Nick Vlassis). Paper accepted by CMAME [URL] 4. Crystal plasticity with precipitation creeping, crack growth and healing in rock salt (presented by associate research scientist Dr. Ran Ma). Paper accepted in CMAME [URL] 5. Domain Partitioning MPM for thermomechanical contact mechanics with fragmentation (presented by PhD student Mian Xiao). Paper under review. 6. ILS-MPM: an implicit level-set-based material point method for contact mechanics (presented by former postdoctoral research scientist, now associate professor of Chinese Academy of Sciences, Prof. Chuanqi Liu). Paper accepted in CMAME [URL] 7. Digital rock physics via FFT Solver (presented by PhD student Zeyu Xiong). 8. Numerical Investigation on freezing and thawing of saturated soil (presented by postdoc research scientist Dr. Qing Yin). Title: A kd-tree-accelerated hybrid data-driven/model-based approach for poroelasticity problems with multi-fidelity multi-physics dataata Abstract: We present a hybrid model/model-free data-driven approach to solve poroelasticity problems. Extending the data-driven modeling framework originated from Kirchdoerfer & Ortiz 2016, we introduce one model-free and two hybrid model-based/data-driven formulations capable of simulating the coupled diffusion-deformation of fluid-infiltrating porous media with different amounts of available data. To improve the efficiency of the model-free data search, we introduce a distance-minimized algorithm accelerated by a k-dimensional tree search. To handle the different fidelities of the solid elasticity and fluid hydraulic constitutive responses, we introduce a hybridized model in which either the solid and the fluid solver can switch from a model-based to a model-free approach depending on the availability and the properties of the data. Numerical experiments are designed to verify the implementation and compare the performance of the proposed model to other alternatives. Preprint Link: [URL] Short Video Introduction:  PhD student Hyoung Suk Suh has been selected as a top 10 finalist for the 2021 Presidential Awards for Outstanding Teaching by a Graduate Student Instructor. Hyoung Suk was a teaching assistant for the soil mechanics course for the last spring semester, and was selected among nearly 500 candidates from across the University. Congratulations, Hyoung Suk for this important distinction! 
PhD student Nick Vlassis passed the qualification exam. Nick's work focuses on incorporating geometric learning for computational plasticity problems with special emphasis on applications related to polycrystalline and energetic materials. In the proposal presentation, Nick presented the work of two of his recent papers published in CMAME (see list below). Nick also recently received the WCCM Fellowship to attend the conference at Paris but the meeting has been converted into virtual format due to the pandemic (see video below). Congratulations for this accomplishment, Nick!
Reference:
Link for the seminar: https://lnkd.in/ePAJrUYPredicting the hysteresis retention behaviors of wetted porous media with a hand-crafted model can be a difficult task, especially for deformable porous media undergoing multiple wetting and drying cycles. In this, work, we introduce a model-free reinforcement learning algorithm that functions as an AI agent to design a recurrent neural network that predicts the water recurrent of a porous medium. As such, the AI agent may conduct numerous trial-and-errors to fine-tune the hyperparameters and design the neural network that yields the optimal performance. Preprint available at [URL].
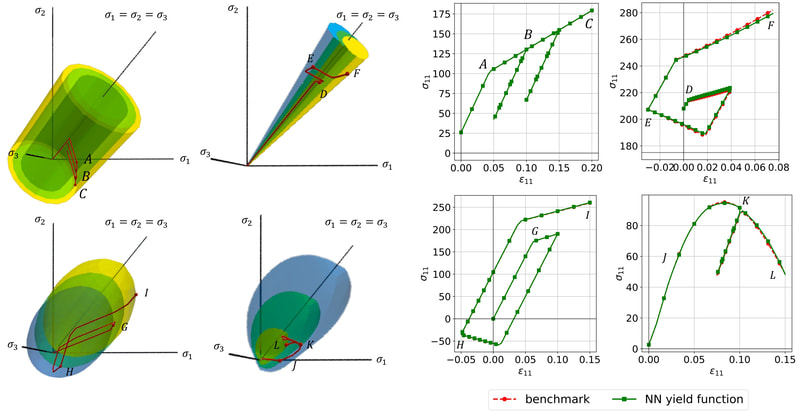
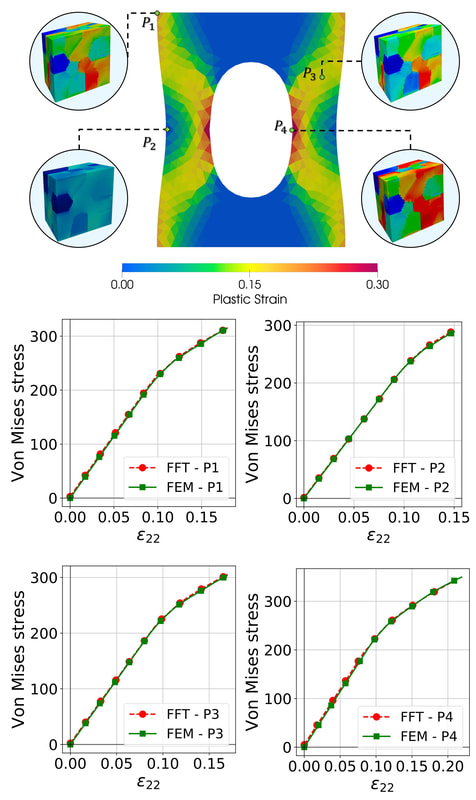
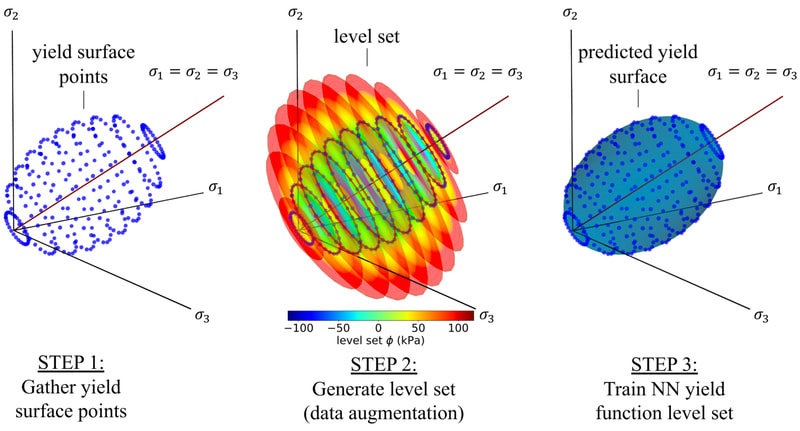
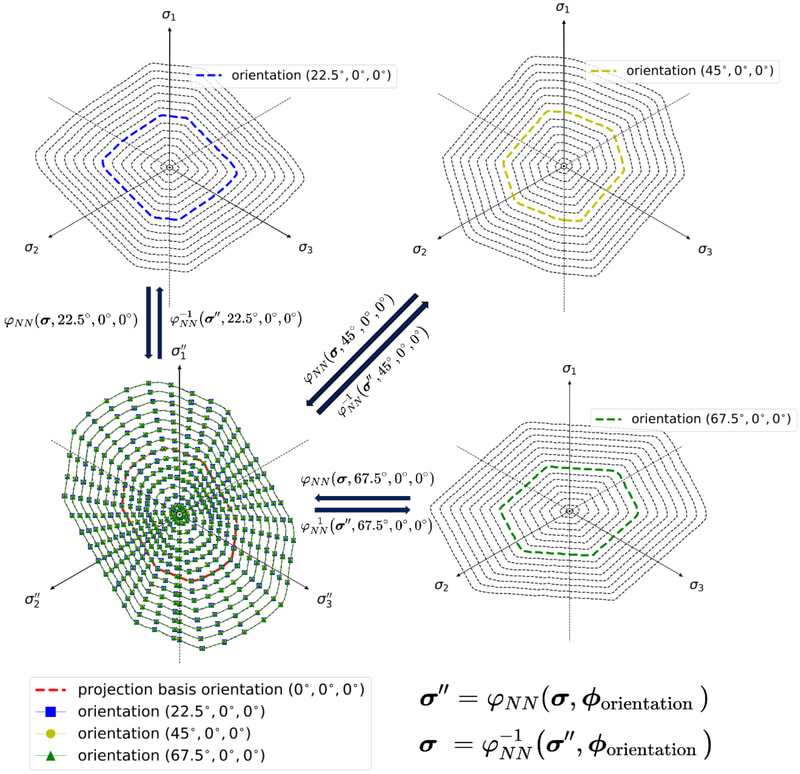
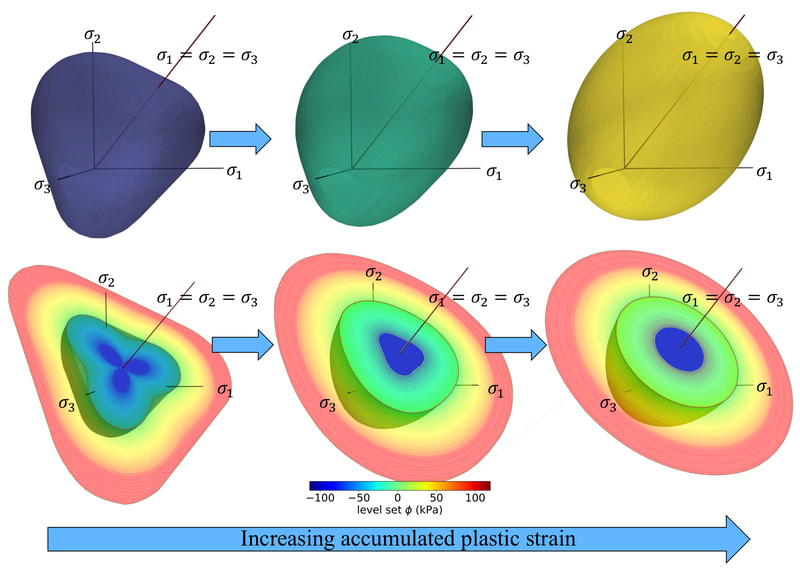
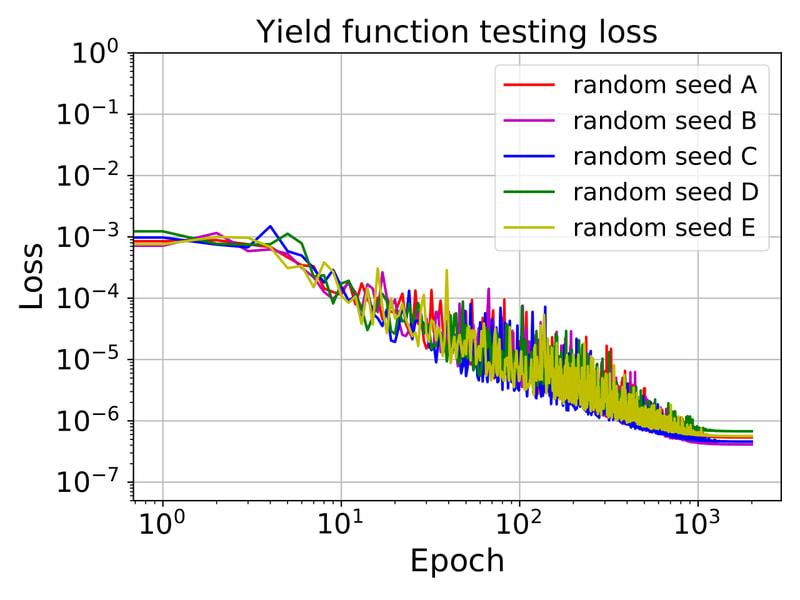
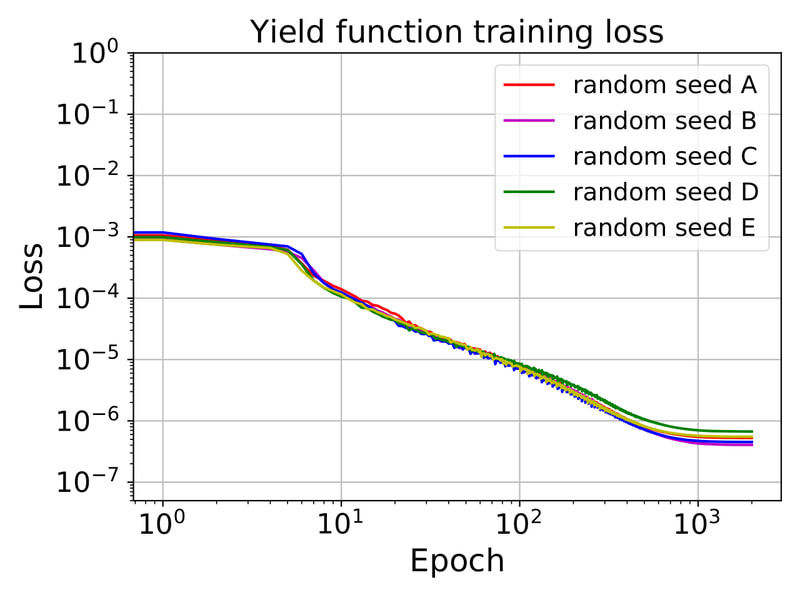
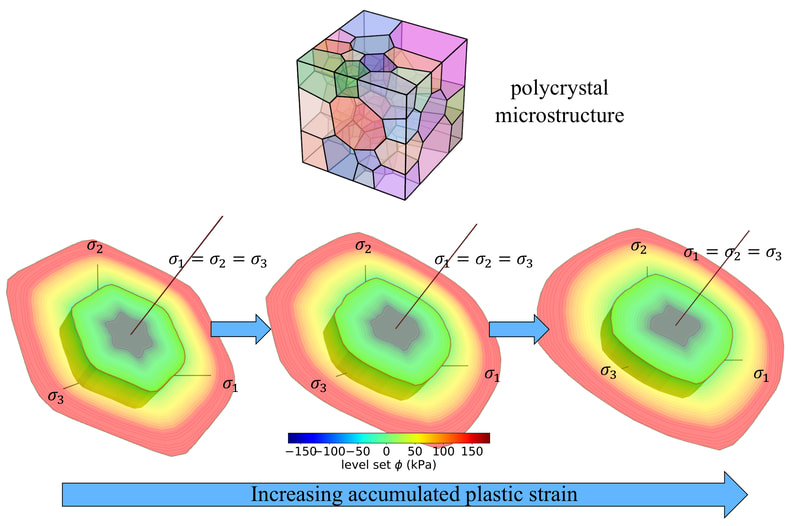
In this work, our goal is to create a generic meta-model that generates constitutive laws for any rate-independent elastoplastic solid with non-vanishing yield surface. Instead of introducing complex neural network to facilicate the machine learning, we break down the process of writing constitutive laws into multiple parts (elasticity, yield surface evolution and plastic flow) each associated with a supervised learning problem designed for generating functionals with properties. This meta-model enable us to (1) more effectively explore the parametric space (i.e. knowing which experiments will improve the model performance), (2) discover previously unknown hardening/softening mechanisms (e.g. any deformation and translation of the yield surface in the principal stress space and the extension to general stress space), and (3) enforce/examine thermodynamic constraints (e.g. Drucker's Postulate) #machinelearning4mechanics #materialmodels. Preprint available [here]. An immersed phase field fracture model for microporomechanics with Darcy–Stokes flow
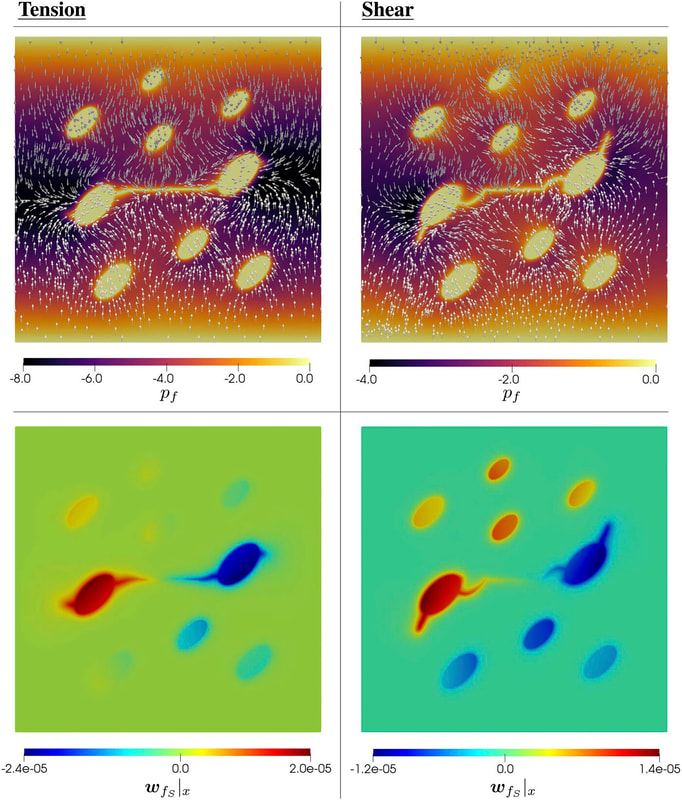
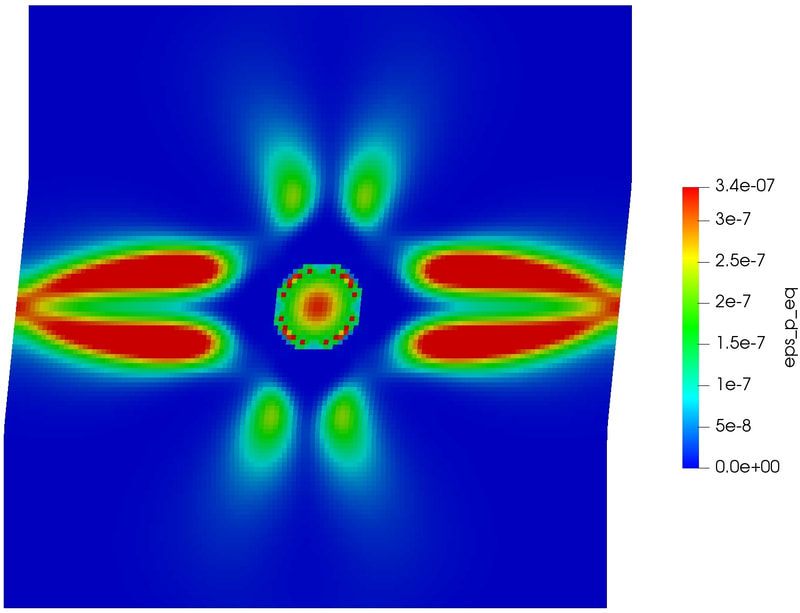
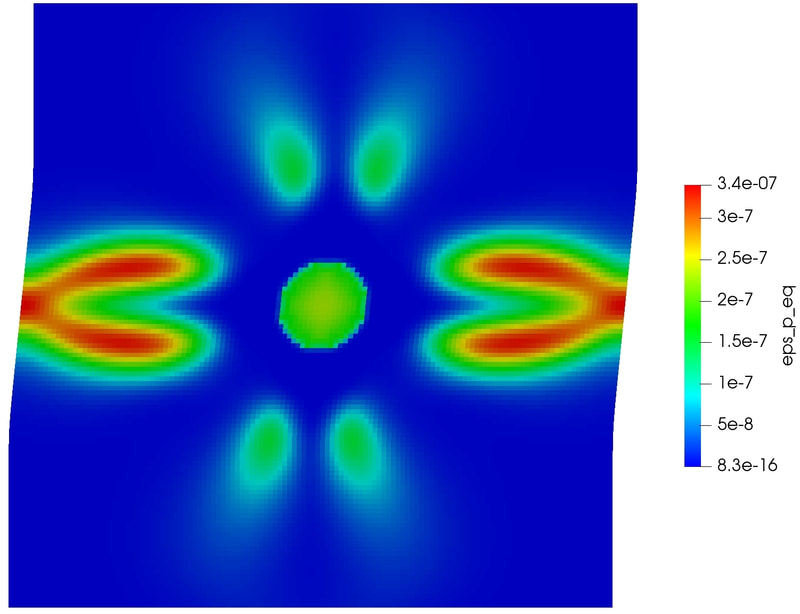
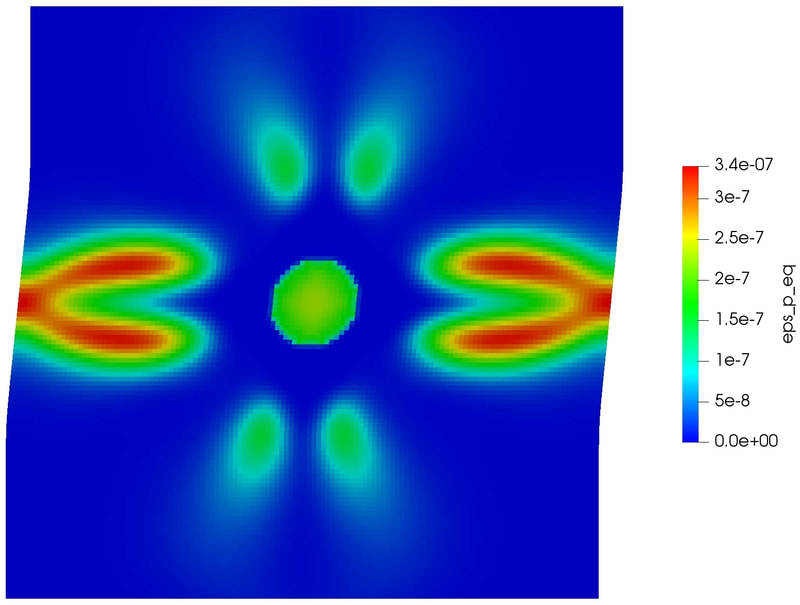
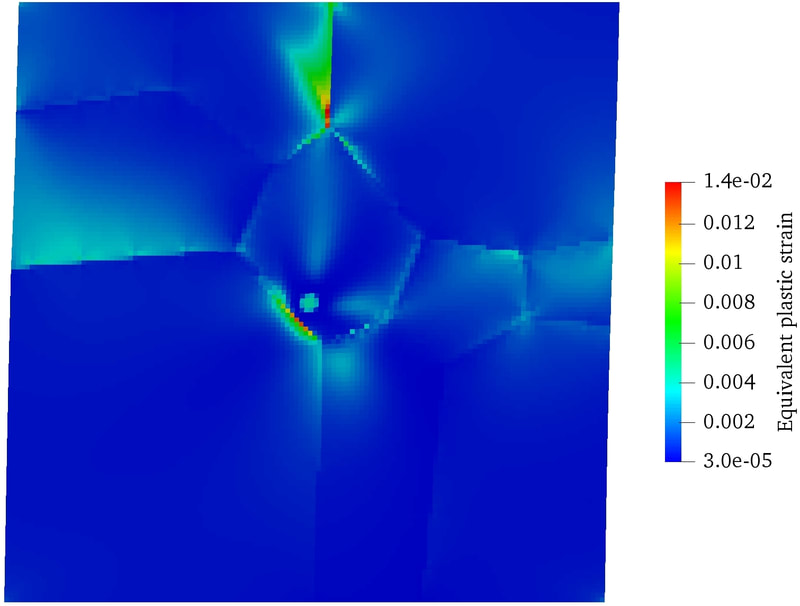
Physics of Fluids 33, 016603 (2021); https://doi.org/10.1063/5.0035602 Hyoung Suk Suh (서형석) and WaiChing Sun (孫維正) ABSTRACT This paper presents an immersed phase field model designed to predict the fracture-induced flow due to brittle fracture in vuggy porous media. Due to the multiscale nature of pores in the vuggy porous material, crack growth may connect previously isolated pores, which leads to flow conduits. This mechanism has important implications for many applications such as disposal of carbon dioxide and radioactive materials and hydraulic fracture and mining. To understand the detailed microporomechanics that causes the fracture-induced flow, we introduce a new phase field fracture framework where the phase field is not only used as an indicator function for damage of the solid skeleton but also used as an indicator of the pore space. By coupling the Stokes equation that governs the fluid transport in the voids, cavities, and cracks and Darcy’s flow in the deformable porous media, our proposed model enables us to capture the fluid–solid interaction of the pore fluid and solid constituents during crack growth. Numerical experiments are conducted to analyze how the presence of cavities affects the accuracy of predictions based on the homogenized effective medium during crack growth. For some polycrystalline materials such as austenitic stainless steel, magnesium, TATB, and HMX, twinning is a crucial deformation mechanism when the dislocation slip alone is not enough to accommodate the applied strain. To predict this coupling effect between crystal plasticity and deformation twinning, we introduce a mathematical model and the corresponding monolithic and operator splitting solver that couples the crystal plasticity material model with a phase field twining model such that the twinning nucleation and propagation can be captured via an implicit function. While a phase-field order parameter is introduced to quantify the twinning induced shear strain and corresponding crystal reorientation, the evolution of the order parameter is driven by the resolved shear stress on the twinning system. To avoid introducing an additional set of slip systems for dislocation slip within the twinning region, we introduce a Lie algebra averaging technique to determine the Schmid tensor throughout the twinning transformation. Three different numerical schemes are proposed to solve the coupled problem, including a monolithic scheme, an alternating minimization scheme, and an operator splitting scheme. Three numerical examples are utilized to demonstrate the capability of the proposed model,
as well as the accuracy and computational cost of the solvers. [preprint] There are many journal articles dedicated to constitutive models that show good matches on selected data. However, how useful are these models if we don't report or know their weakness? Our recently accepted CMAME paper uses deep reinforcement learning and game theory to explore this important question. By conceptualizing the efforts to validating and falsifying the model as a competing activities, we introduce AI agents to compete against each others to explore each others' weakness and through competition improving the resultant model and finding the Nash equilibrium that represents the limits of the state-of-the-art of each model, hand-crafted or AI-generated. The interesting aspect is that this competition can be applied to any material laws and data set. Please consider submit data/model to us and we can validate and falsify the model for you. More information can be found in the preprint [PDF]. The lectures for the entire 3-day workshop can be found at the official website of ALERT. alertgeomaterials.eu/2020/10/videos-of-the-doctoral-school-2020/ Special thanks to the organizers, Professors Wei Wu and Manuel Pastor, and the colleagues who attend the talks. PhD student Hyoung Suk Suh passed the qualification exam. His work is on modeling the thawing and freezing of frozen porous media. In the proposal talk, Hyoung Suk introduces the mathematical framework requires to simulate the freezing and thawing of porous media at the pore scale (see the rehearsal Youtube Video below). Since joining the research group in Fall 2018, Hyoung Suk has published two journal articles and one conference paper.
H.S. Suh, D. O'Conner, W.C. Sun, A phase field model for cohesive fracture in micropolar continua, Computer Methods in Applied Mechanics and Engineering, doi:10.1016/j.cma.2020.113181, 2020. H.S. Suh, W.C. Sun, An open source FEniCS implementation of a phase field fracture model for micropolar continua, International Journal of Multiscale Computational Engineering, doi:10.1615/IntJMultCompEng.2020033422, 2019. [open source code] H.S. Suh, W.C. Sun, An immersed phase field fracture model in fluid-infiltrating porous media with evolving Beavers-Joseph-Saffman condition, 2nd International Conference on Energy Geotechnics, La Jolla, California, USA, 2021. Congratulations, Hyoung Suk!  I am excited to announce that our PhD student Eric Bryant has successfully defended his dissertation "Capturing Evolving Size-Dependent Anisotropy from Brittle Fracture to Plasticity for Geological Materials" and will join Los Alamos National Laboratory as postdoc research associate. His primary appointment will be with the fluid dynamics and solid mechanics group of the Theoretical Division (T-3). During his tenure in the Sun research group, Eric has been awarded the Presidential Fellowship and the Guggenheim Fellowship. His PhD work focuses on modeling the size effect of evolving anisotropy of fracture and plastic deformation. Traditionally, one may introduce scaling law to incorporate how shear and tensile strengths depend on the size of the specimen. In his work, the main focus is also to investigate how does the rotation among the principal directions of the elastic strain, tensorial internal variables and stress tensor evolves across length scales and during the deformation process. He is the authors of 4 journal articles and one manuscript very close to completion. Among them, three of them published in Computer Methods in Applied Mechanics and Engineering, and one in International Journal of Fracture as listed below. Congratulations, Eric! Published work:
Author: Nikolas Vlassis, WaiChing Sun
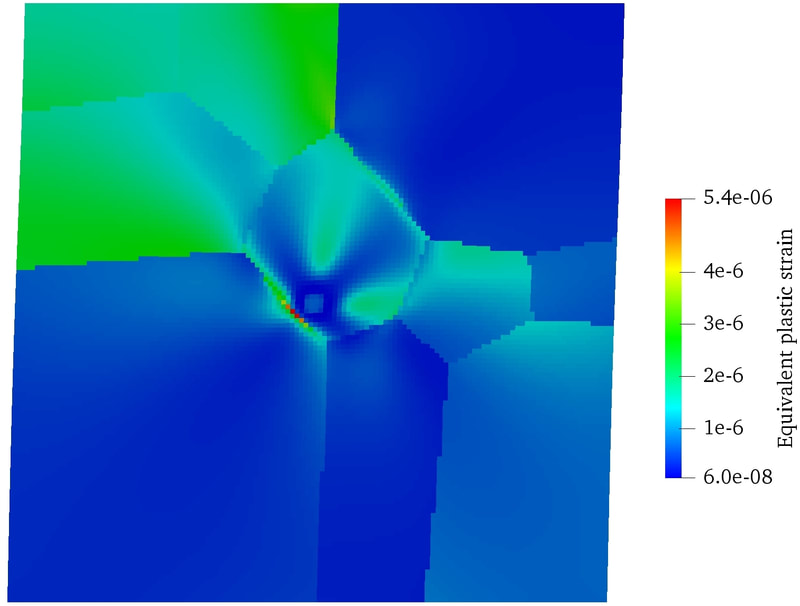
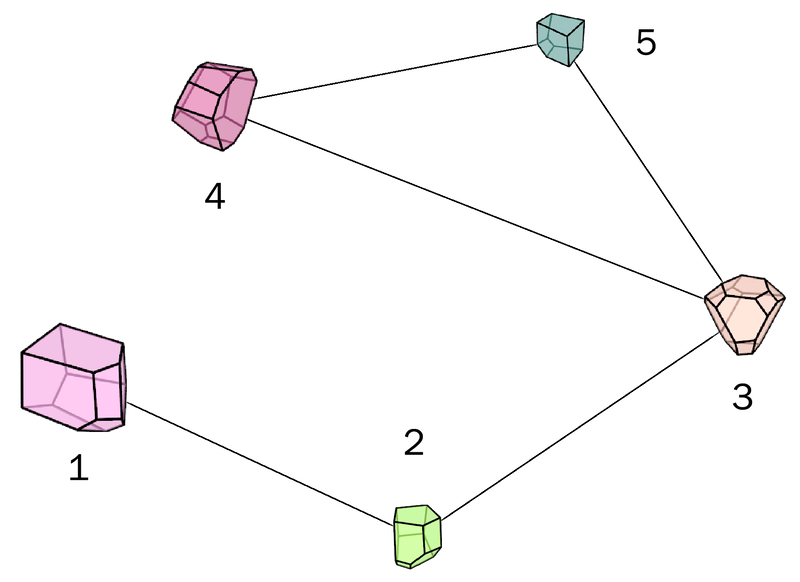
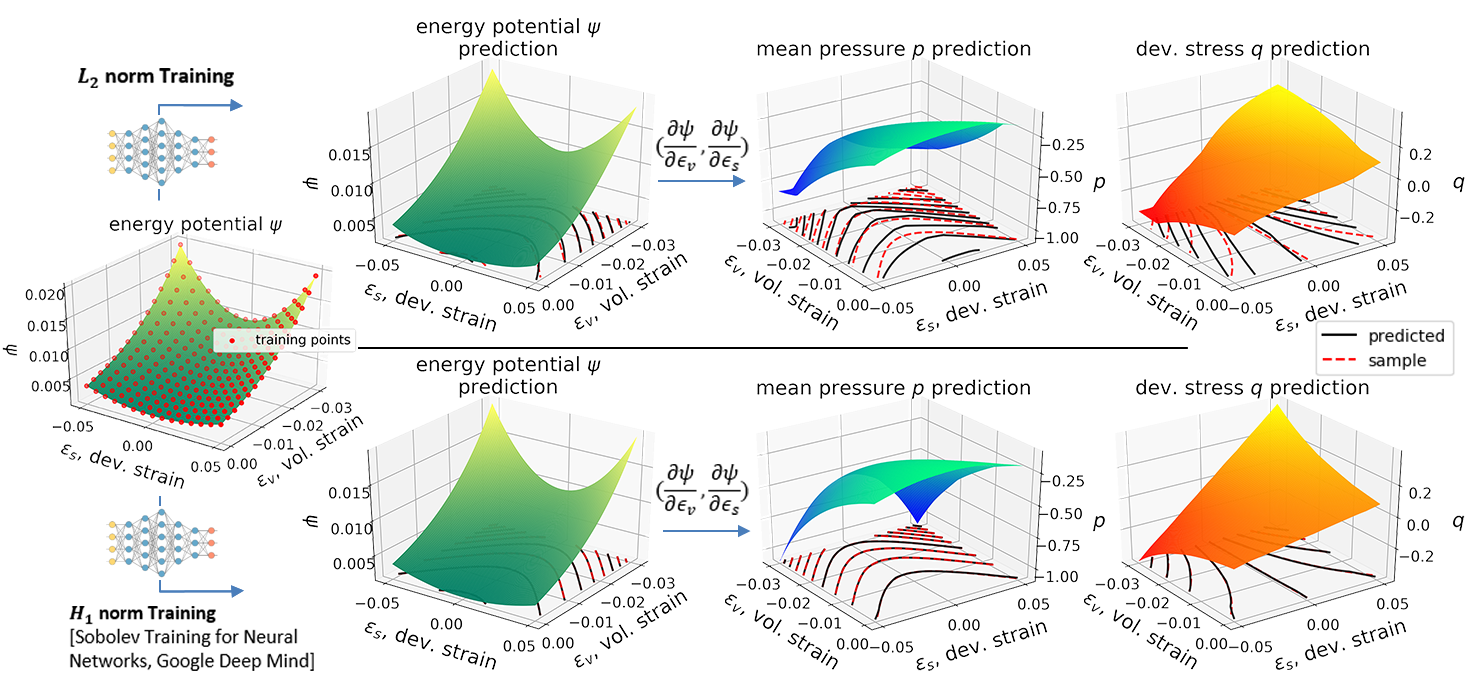
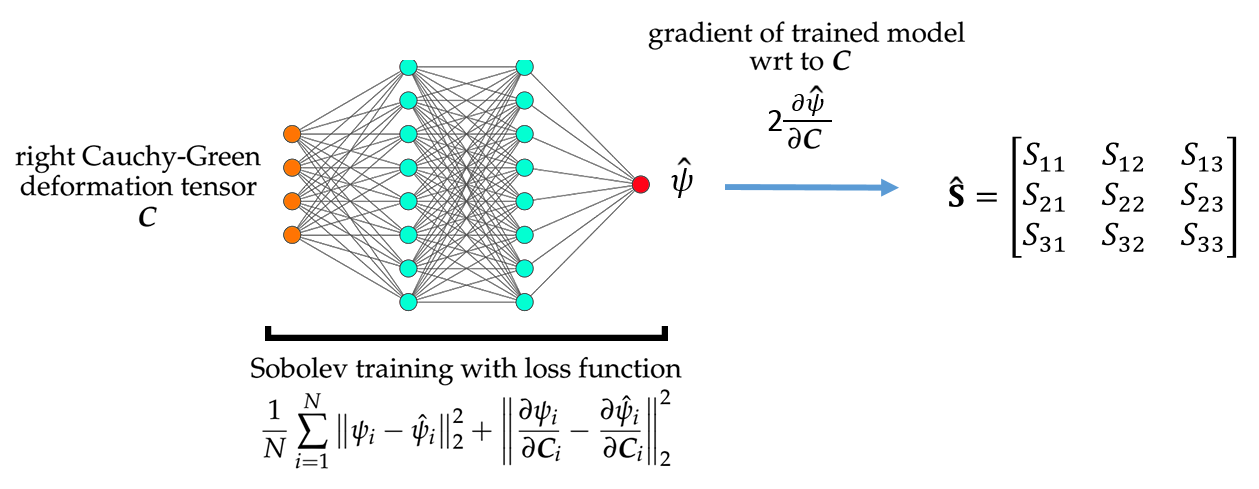
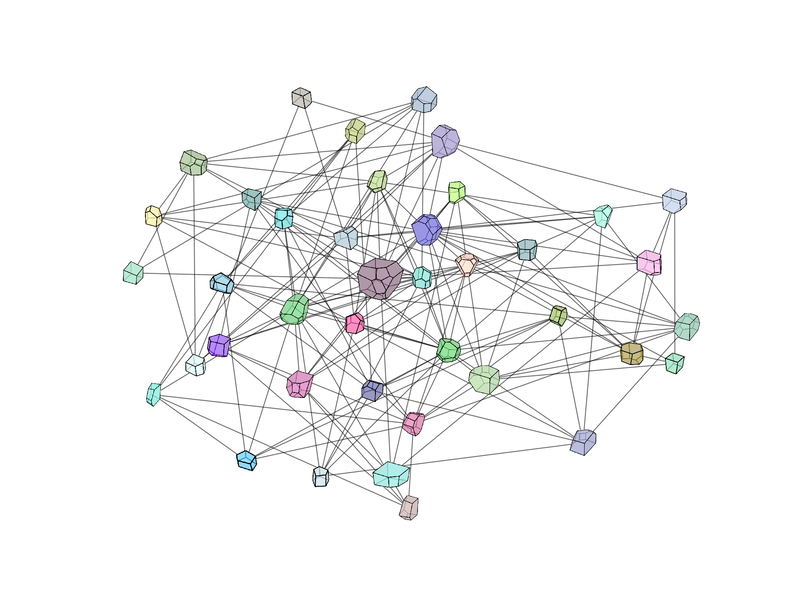
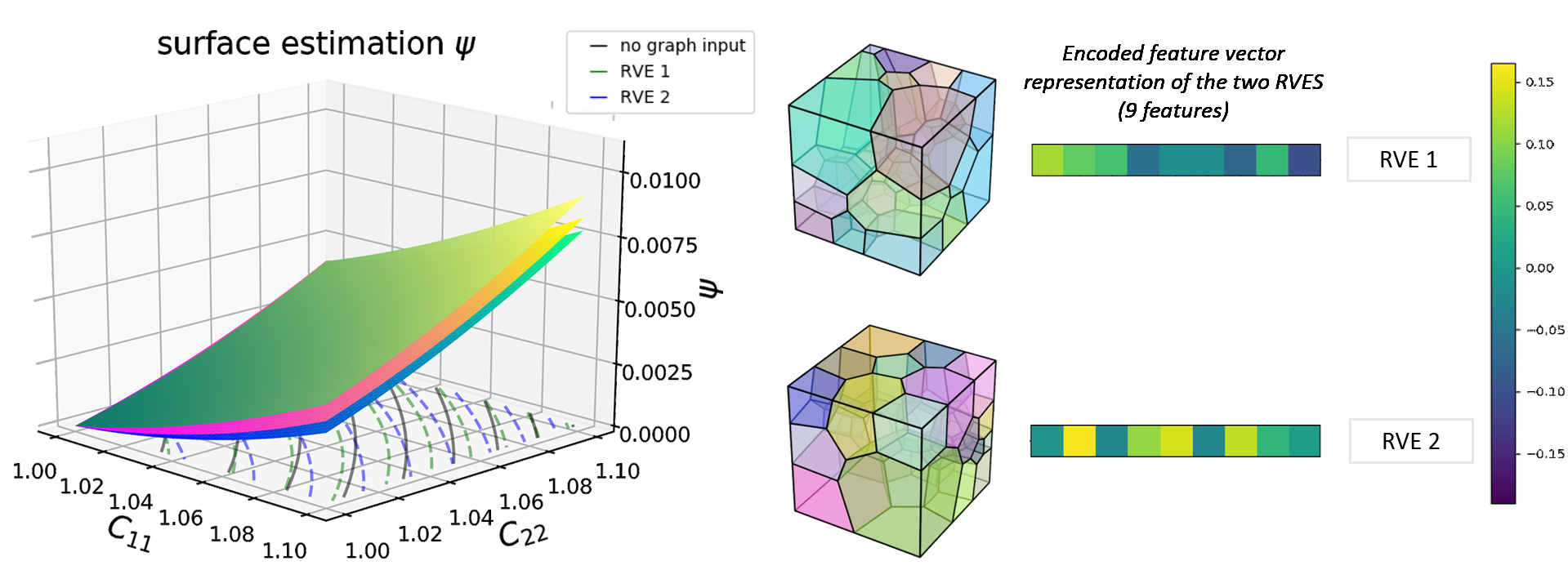
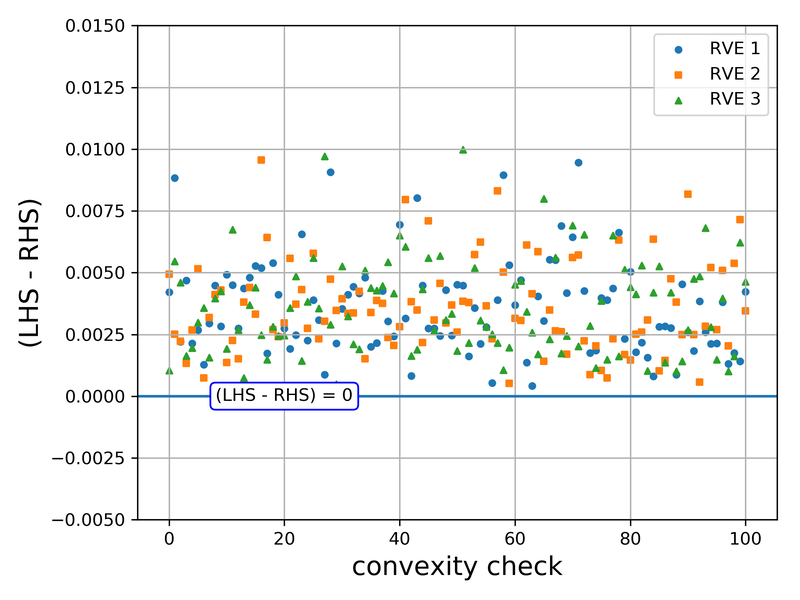
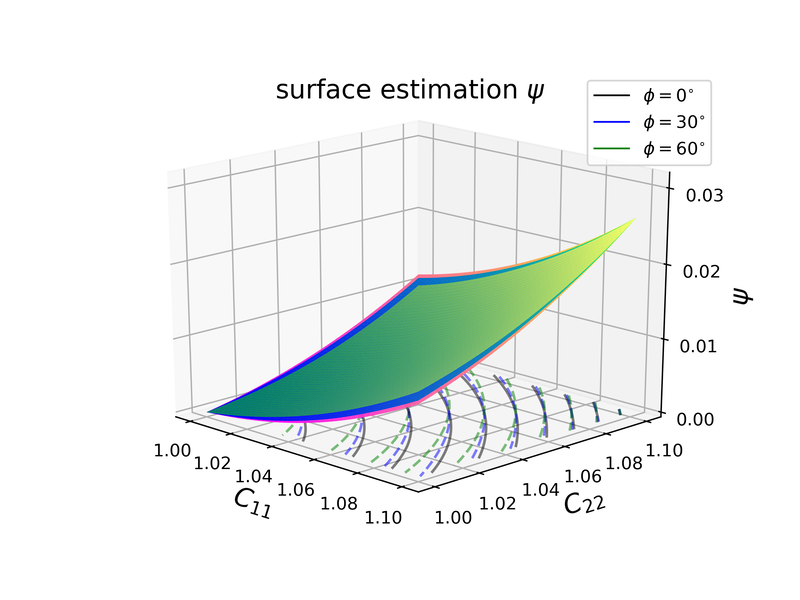
Abstract: We present a machine learning approach that integrates geometric deep learning and Sobolev training to generate a family of finite strain anisotropic hyperelastic models that predict the homogenized responses of polycrystals previously unseen during the training. While hand-crafted hyperelasticity models often incorporate homogenized measures of microstructural attributes, such as the porosity or the averaged orientation of constitutes, these measures may not adequately reflect the topological structures of the attributes. We fill this knowledge gap by introducing the concept of the weighted graph as a new high-dimensional descriptor that represents topological information, such as the connectivity of anisotropic grains in an assemble. By leveraging a graph convolutional deep neural network in a hybrid machine learning architecture previously used in Frankel et al. 2019, the artificial intelligence extracts low-dimensional features from the weighted graphs and subsequently learns the influence of these low-dimensional features on the resultant stored elastic energy functionals. To ensure smoothness and prevent unintentionally generating a non-convex stored energy functional, we adopt the Sobolev training method for neural networks such that a stress measure is obtained implicitly by taking directional derivatives of the trained energy functional. Results from numerical experiments suggest that Sobolev training is capable of generating a hyperelastic energy functional that predicts both the elastic energy and stress measures more accurately than the classical training that minimizes L2 norm. Verification exercises against unseen benchmark FFT simulations and phase-field fracture simulations using the geometric learning generated elastic energy functional are conducted to demonstrate the quality of the predictions. [manuscript]
|
Group NewsNews about Computational Poromechanics lab at Columbia University. Categories
All
Archives
July 2023
|




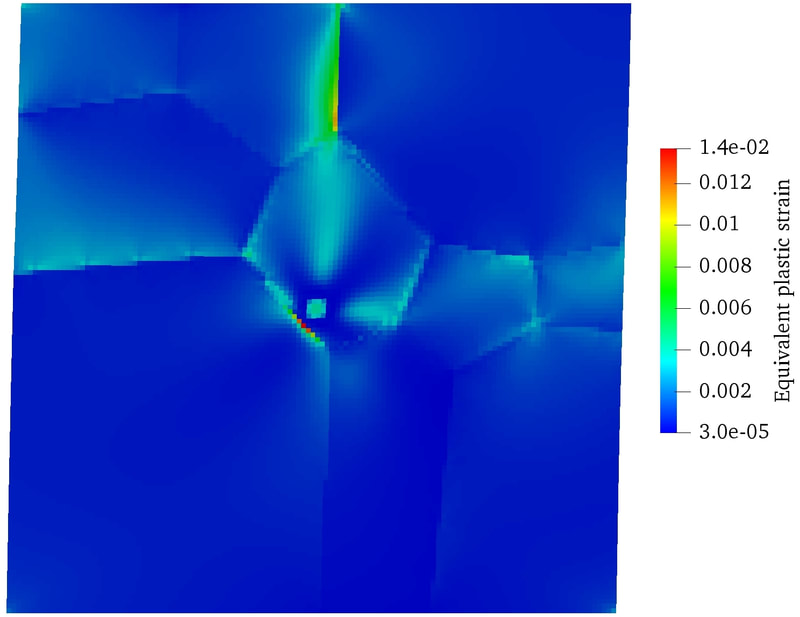
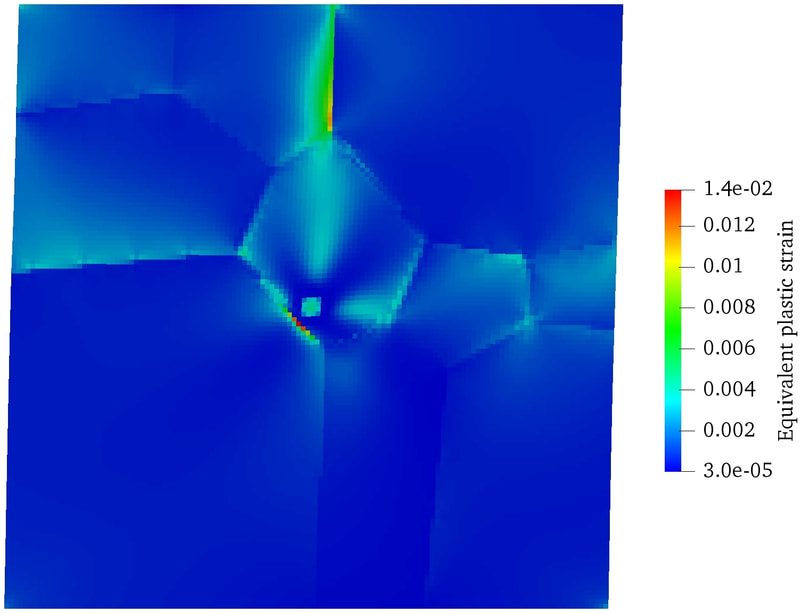
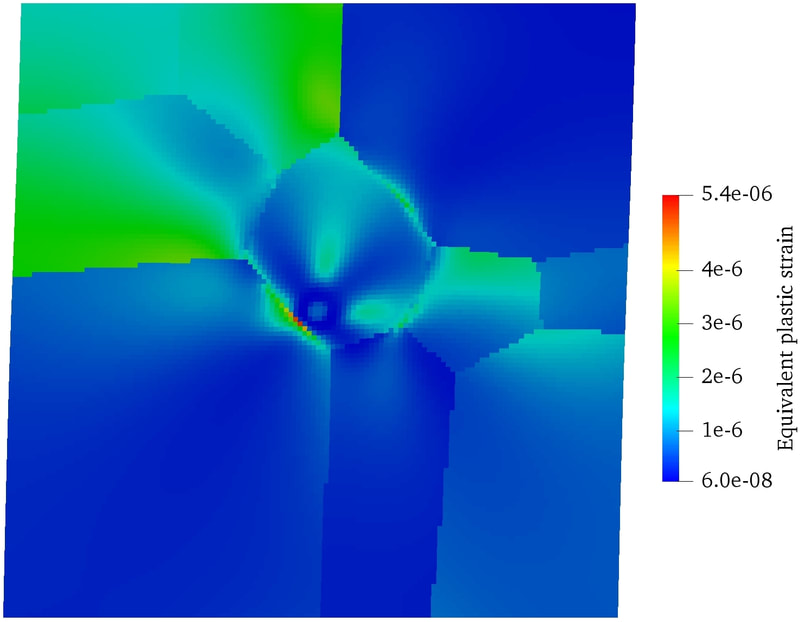
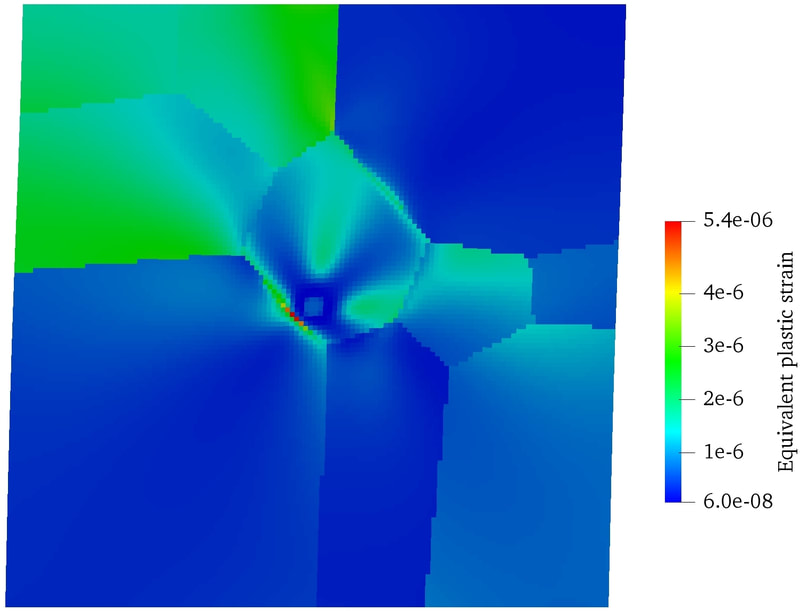


 RSS Feed
RSS Feed