Part I of our paper series on geometric learning and Sobolev training for computational mechanics has been accepted by CMAME

Author: Nikolas Vlassis, WaiChing Sun
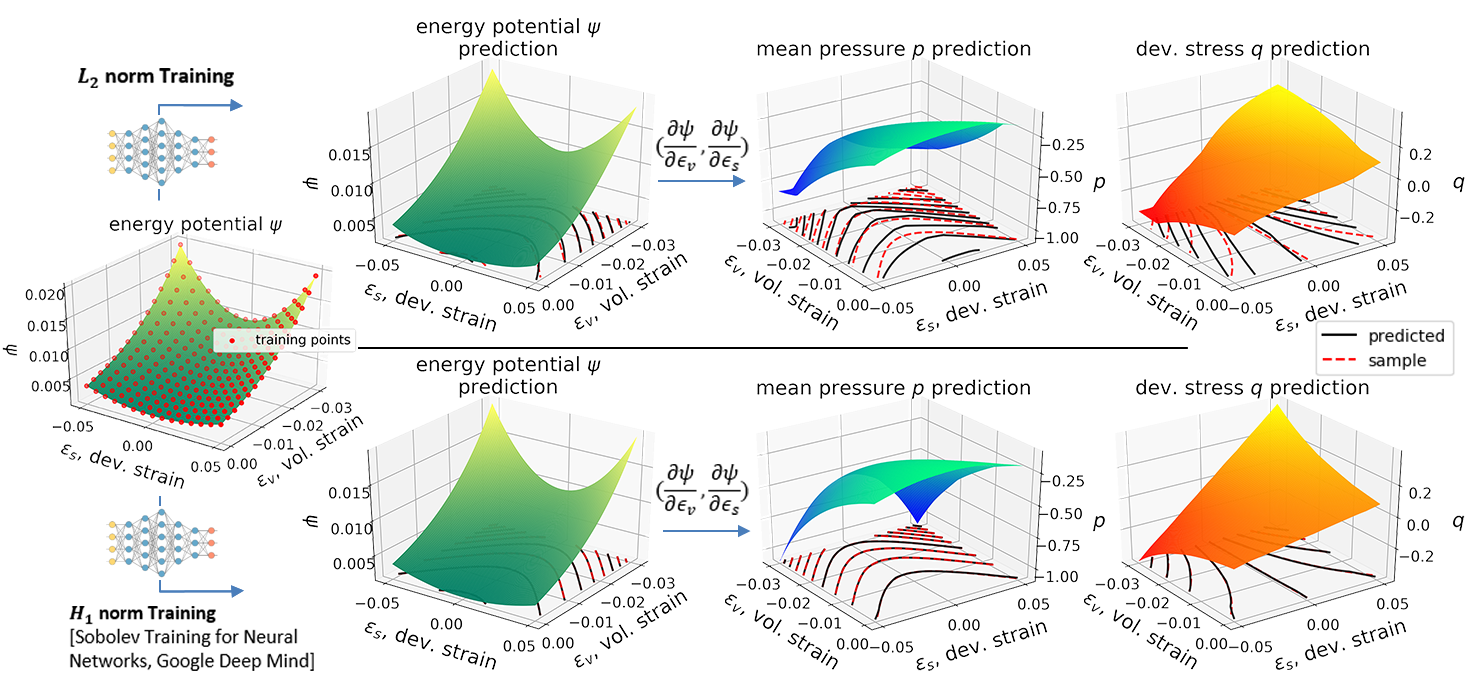
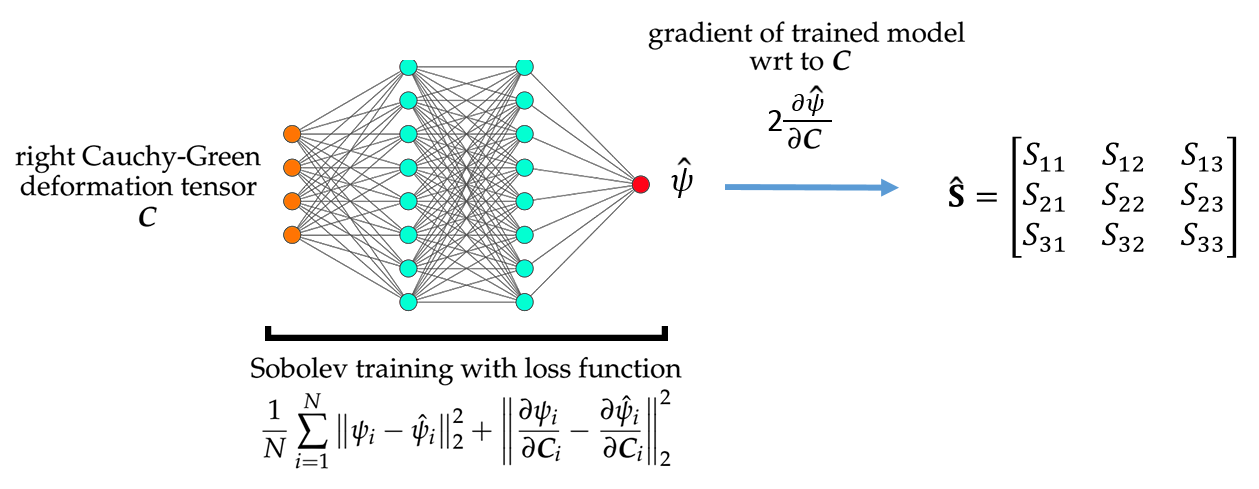
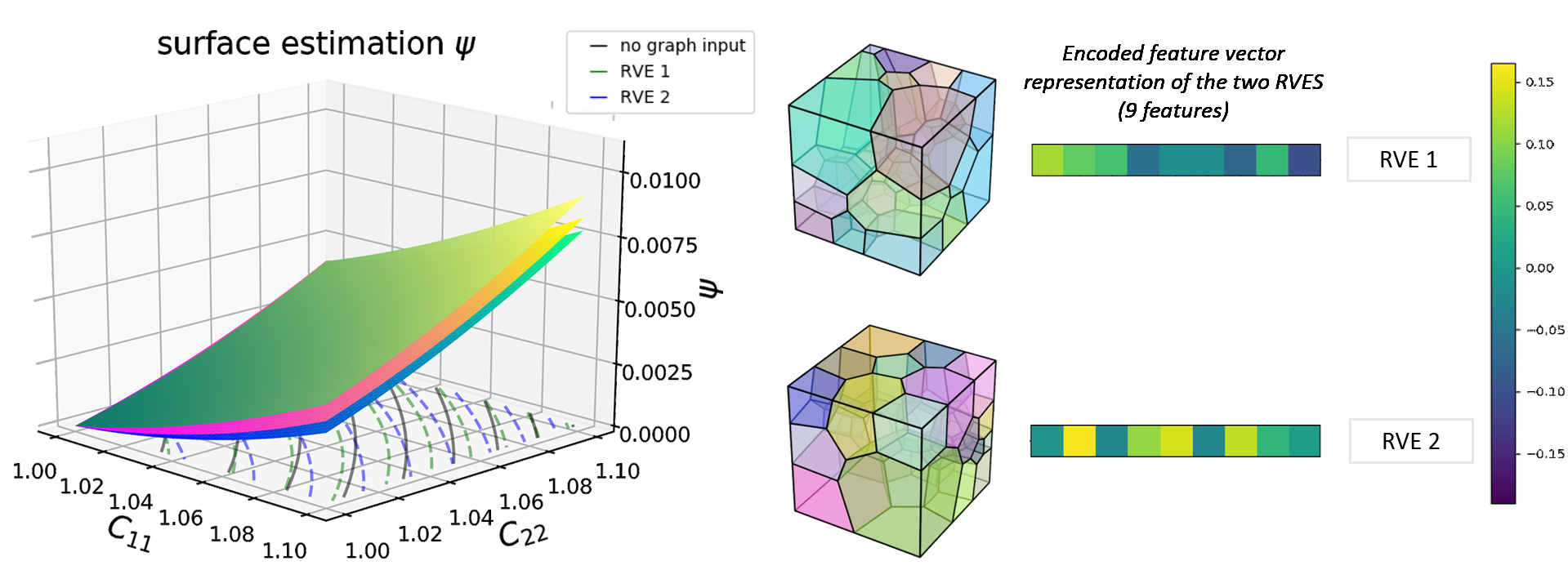
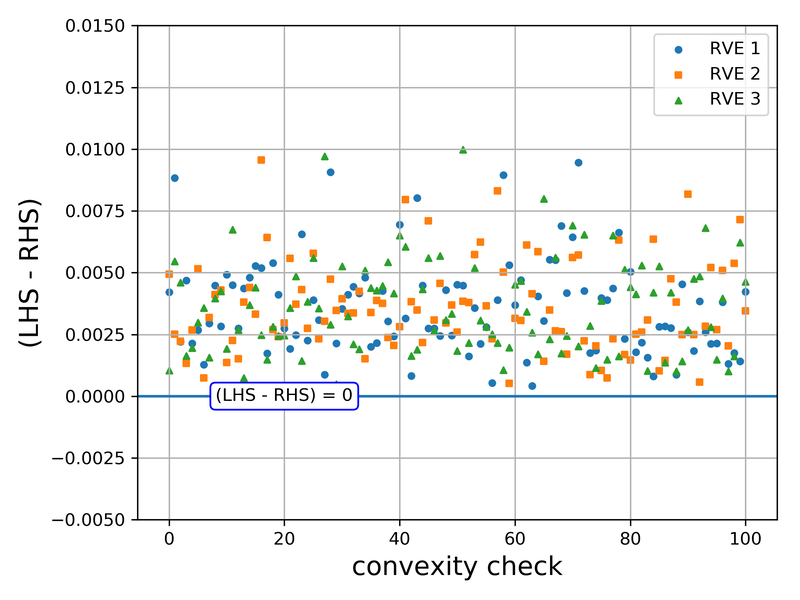
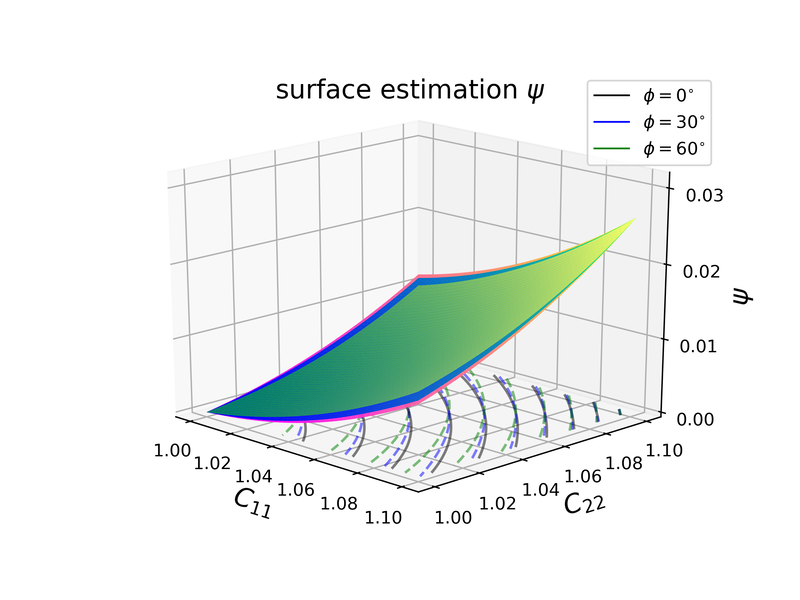
Abstract: We present a machine learning approach that integrates geometric deep learning and Sobolev training to generate a family of finite strain anisotropic hyperelastic models that predict the homogenized responses of polycrystals previously unseen during the training. While hand-crafted hyperelasticity models often incorporate homogenized measures of microstructural attributes, such as the porosity or the averaged orientation of constitutes, these measures may not adequately reflect the topological structures of the attributes. We fill this knowledge gap by introducing the concept of the weighted graph as a new high-dimensional descriptor that represents topological information, such as the connectivity of anisotropic grains in an assemble. By leveraging a graph convolutional deep neural network in a hybrid machine learning architecture previously used in Frankel et al. 2019, the artificial intelligence extracts low-dimensional features from the weighted graphs and subsequently learns the influence of these low-dimensional features on the resultant stored elastic energy functionals. To ensure smoothness and prevent unintentionally generating a non-convex stored energy functional, we adopt the Sobolev training method for neural networks such that a stress measure is obtained implicitly by taking directional derivatives of the trained energy functional. Results from numerical experiments suggest that Sobolev training is capable of generating a hyperelastic energy functional that predicts both the elastic energy and stress measures more accurately than the classical training that minimizes L2 norm. Verification exercises against unseen benchmark FFT simulations and phase-field fracture simulations using the geometric learning generated elastic energy functional are conducted to demonstrate the quality of the predictions. [manuscript]