|
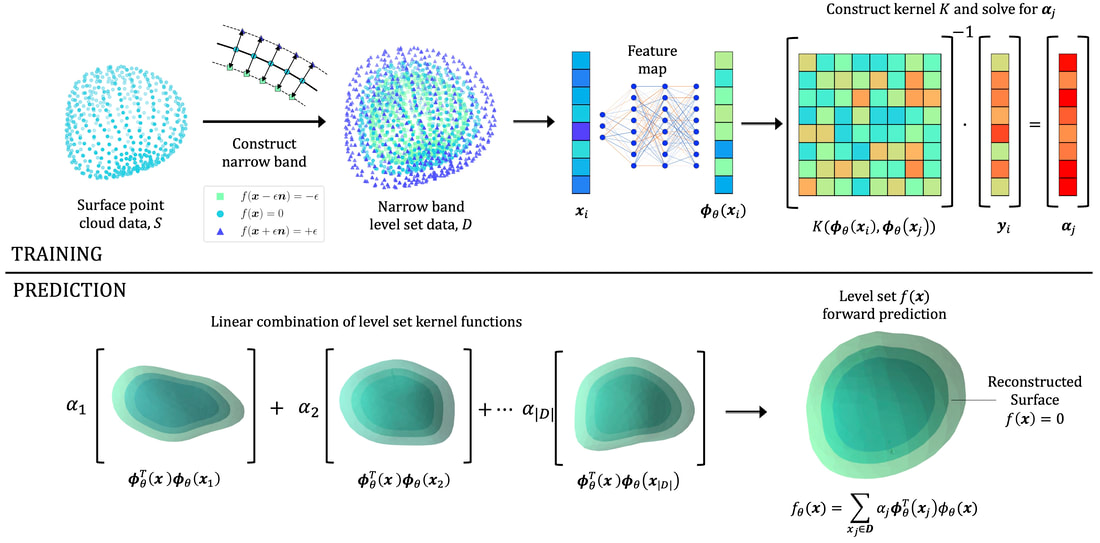
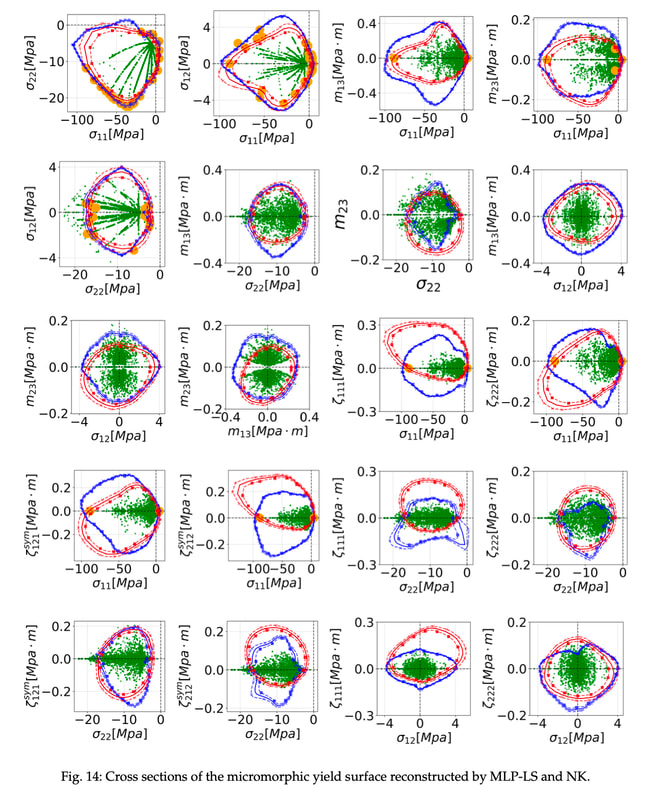
Most of the constitutive laws leverages symmetry to reduce the dimensionality of the models. A classical example is the assumption of material isotropy. However, there are cases in which the minimal dimension of the material models must increase to sufficiently describe the physics. An example is micropolar and micromorphic theories (see below). This increase of dimensionality makes it more difficult to derive constitutive laws manually, as our curve-fitting ability and sense of geometry often not extend beyond 3D. This paper introduces a neural kernel approach to generate high-dimensional micropolar and micromorphic plasticity models. Here we want to leverage the robustness and interpretability of the kernel method afforded by the feature space while generating a data-dependent kernel tailored to our specific need to capture the high-dimensional constitutive responses of the materials with complex internal structures. This treatment provides us with a unified data-driven approach to recognize the pattern of the data (through the data-dependent kernel), regardless of the data dimensions. Combined with a simple kernel ridge regression, we may generate a yield function of arbitrary input space dimensions without explicitly handcrafting the feature space. This trait is important for us to automate the process of generating yield surface from data of dimensions higher than 3, especially when data is sparse. The Figure below shows the learned micromorphic yield surface inferred from RVE projected onto 2D stress components. An interesting aspect we observe is that there could be multiple hypothesized yield surface fits the same data and they can be quite difference. Nevertheless, the feature space obtained from the kernels does seem to provide a regularization that lead to a more convex yield surface, which can be important to ensure thermodynamics consistency. More in-depth discussion can be found by the preprint [URL].
0 Comments
Leave a Reply. |
Group NewsNews about Computational Poromechanics lab at Columbia University. Categories
All
Archives
July 2023
|

 RSS Feed
RSS Feed