Our paper on using manifold embedding to enable distance-minimizing model-free/data-driven simulations for finite elasticity problems has been accepted by JMPS

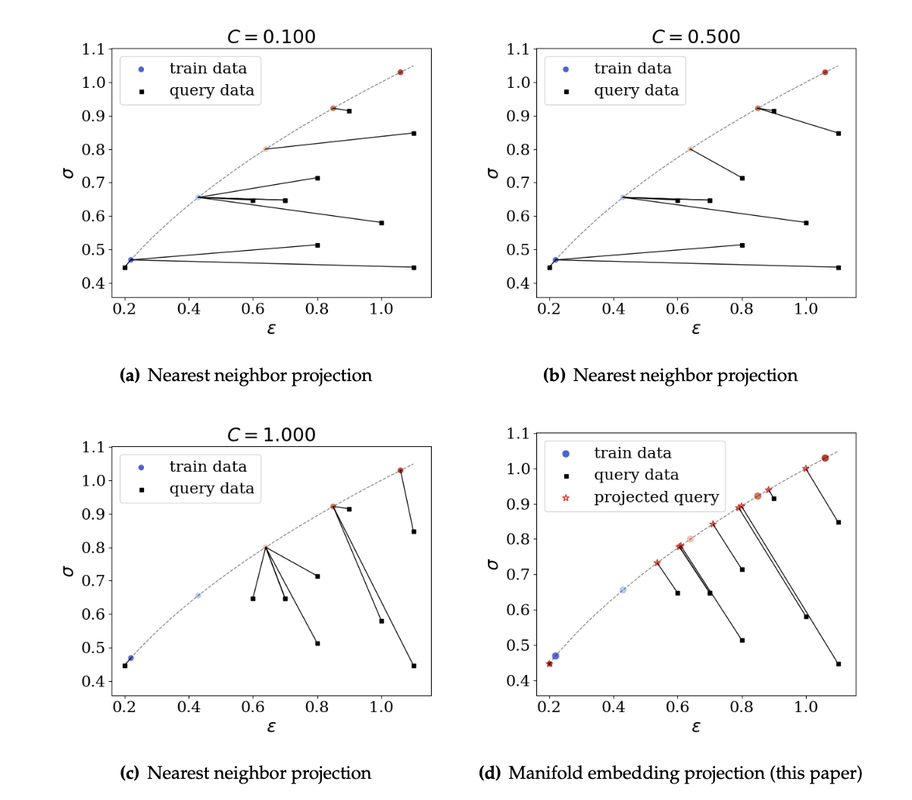
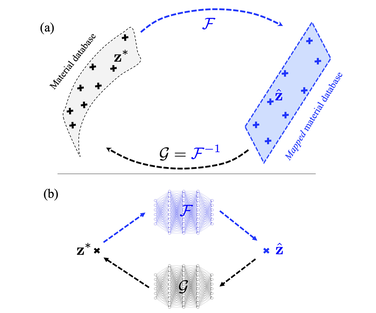
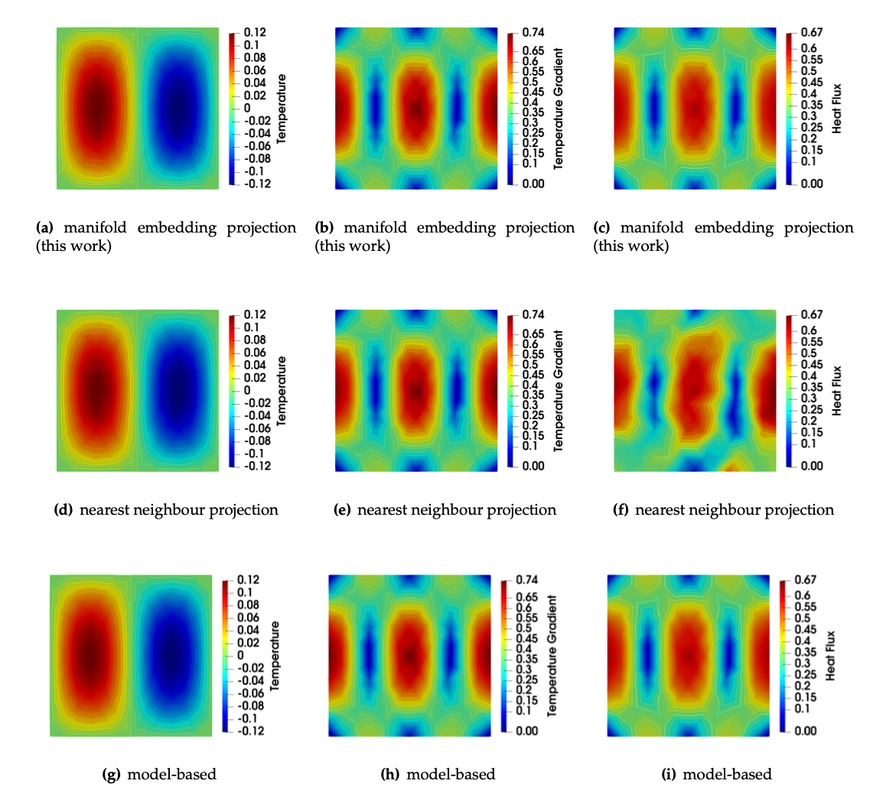
This paper (see the preprint available here) introduces a manifold embedding data-driven paradigm to solve small- and finite-strain elasticity problems without a conventional constitutive law. ​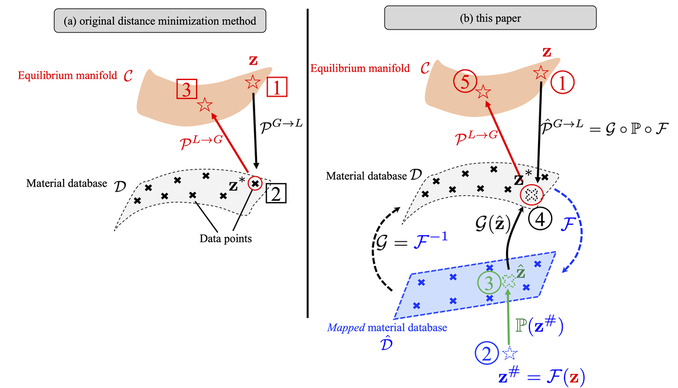

​

---

Traditionally, data-driven paradigm often replace a constitutive law with a search that select an experimental data point that is " the closest" to the balance principle. However, how distance or length is measured remains ambiguous. Often time, an arbitrarily energy norm is chosen, but such a practice has shown to be affected which closest data point is getting selected. In particular, in a nonlinear manifold, the shortest distance between two points and the Euclidean distance can be quite different when they are far apart. Furthermore, the resultant model-free simulation could be sensitive to the chosen norm used to measure distance (see figure below). ​

We follows the classical data-driven paradigm by seeking the solution that obeys the balance of linear momentum and compatibility conditions while remaining consistent with the material data through minimizing a distance measure. Our key point of departure is the introduction of a global manifold embedding as a means to learn the geometrical trend of the constitutive data mathematically represented by a smooth manifold.

Conventionally, an incremental nonlinear constitutive update is sought by solving a sequence of linearized equations that moves along the admissible range of the constitutive law until the solution is found. Instead of doing this, we propose to simply deform the phase space where the nonlinear constitutive law exists such that the resultant constitutive law in the deformed space appear to be linear. 

A pair of neural networks (see below) are trained to learn (1) how to deform this nonlinear constitutive manifold to make it flat (i.e. there is one normal vector everywhere in the deformed hyperplane), and (2) how to deform the hyperplane back into a smooth manifold. Consequently, the flatness of the deformed hyperplane then makes it very easy to measure the distance between a point and the hyperplane, while the inverse map allows us to convert the local search result back into a point in the nonlinear constitutive law. 

By training an invertible neural network to embed the data of an underlying constitutive manifold onto a Euclidean space, we reformulate the local distance-minimization problem such that it replace the computationally intensive combinatorial search to identify the optimal data points closest to the conservation law with a cost-efficient projection step.

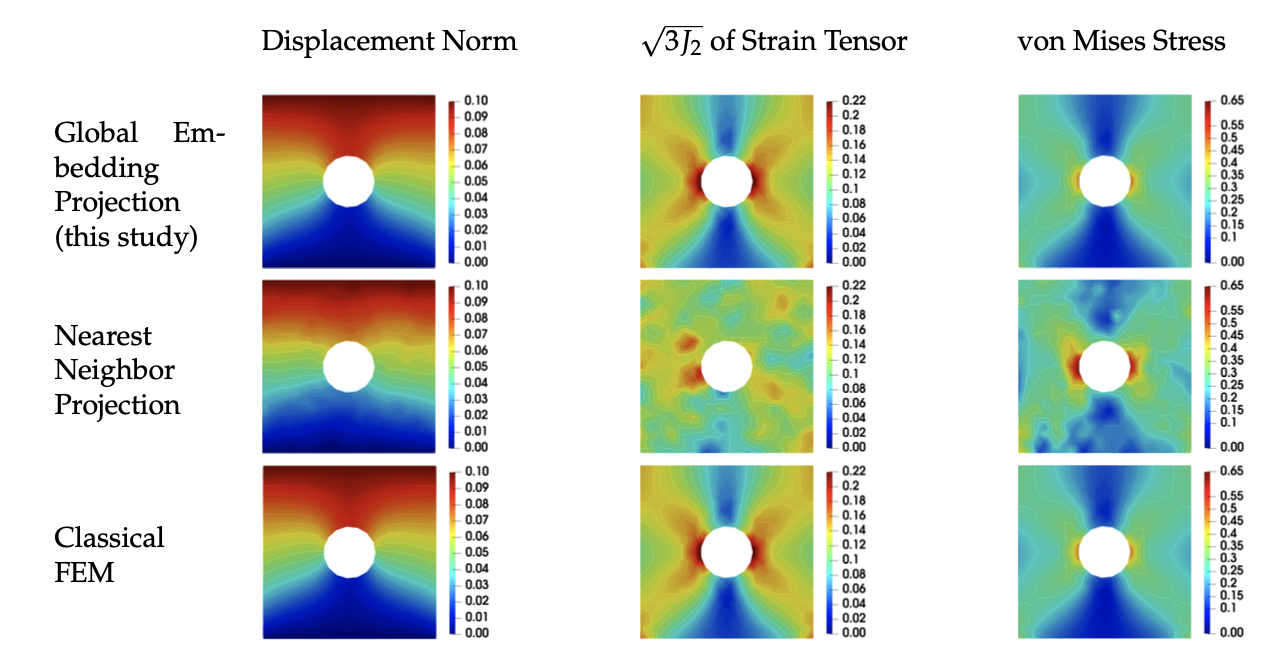
Meanwhile, numerical experiments performed on path-independent elastic materials of different material symmetries suggest that the geometrical inductive bias learned by the neural network is helpful to ensure more consistent predictions when dealing with data sets of limited sizes or those with missing data (see examples below).