Geometric Learning for physics-constrained response surface for geometrically nonlinear shell has been accepted by CMAME

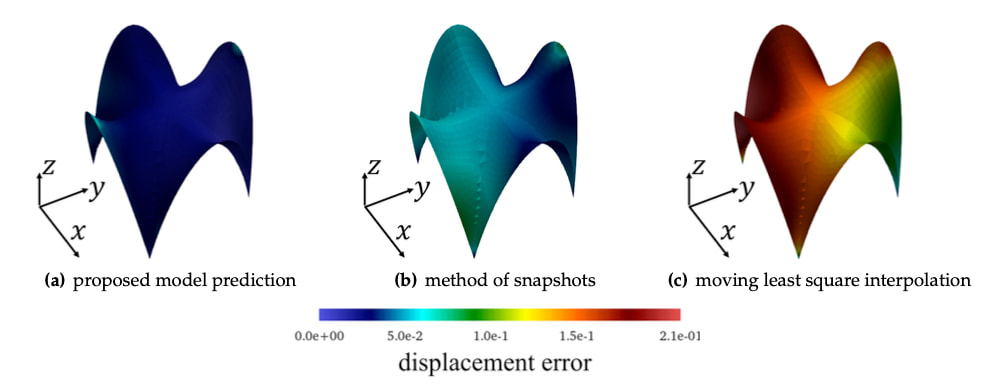
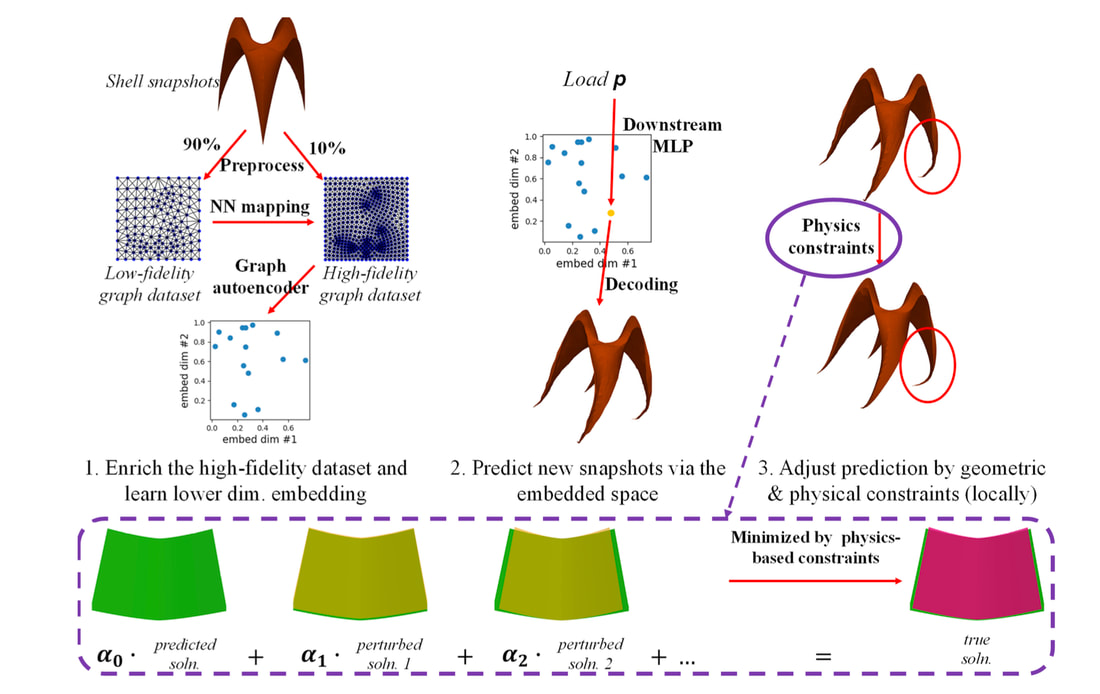
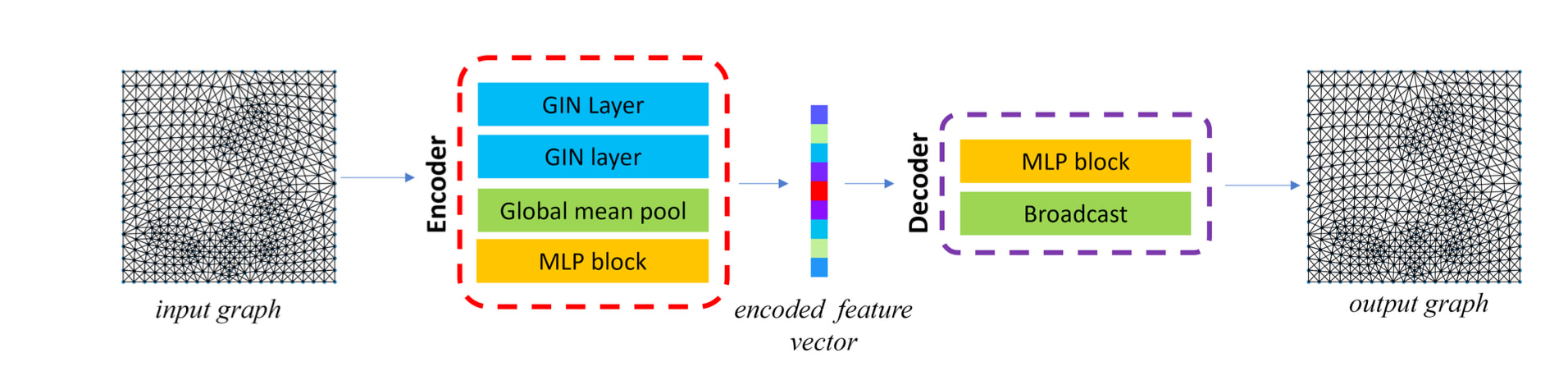
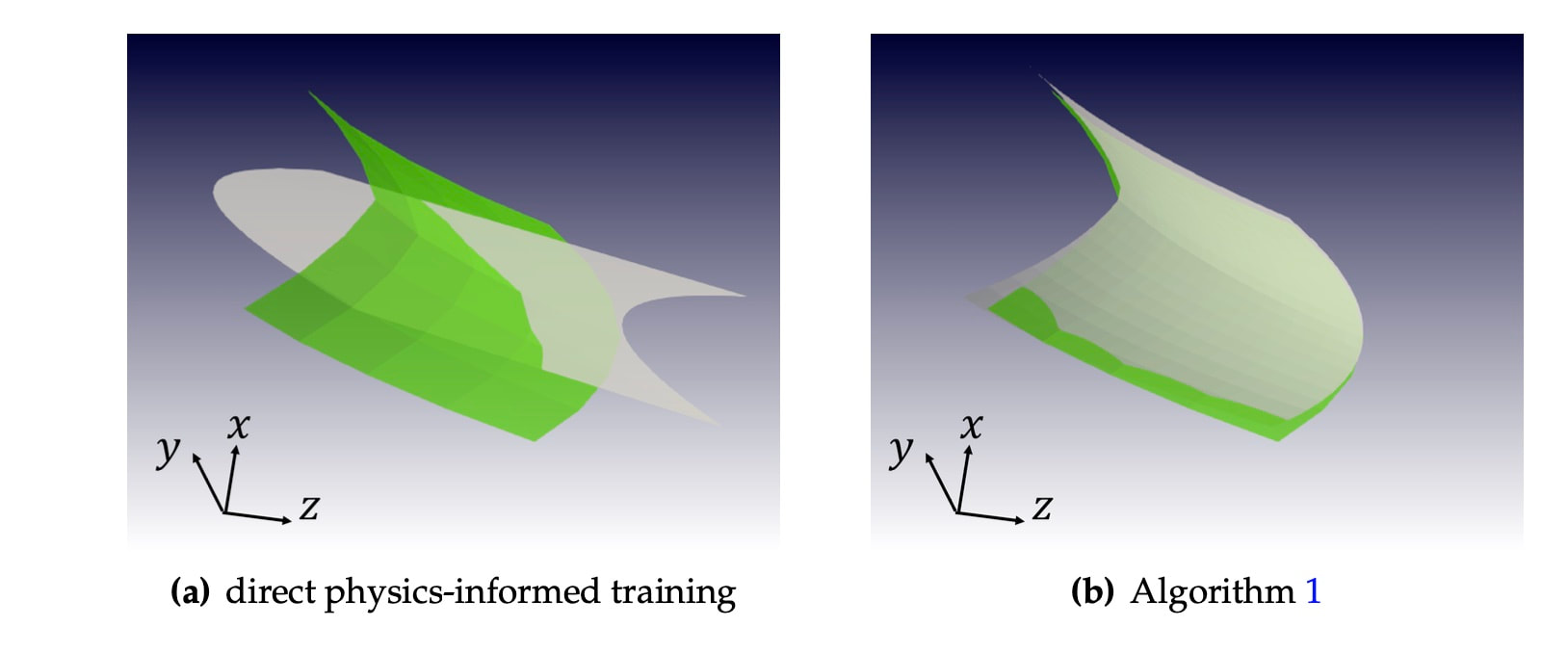
Classical finite element simulation often solves one boundary value problem at a time. However, for many engineering applications, a response surface for a family of boundary value problems is often needed to understand how a structure responds to a variety of external loadings. In principle, run multiple finite element simulations to populate the parametric space and then interpolate the responses. However, due to the high dimensionality of the problems (which is equal to the number of degrees of freedom), the traditional interpolation technique may lead to significant errors (see figure below for the Simo-Fox-Rifai shell).

In this work, we have two goals. First, we want to introduce a technique in which we can use multi-resolution latent space deduced from the weighted graph of finite elements to predict high-fidelity finite element simulations with a mixture of low-fidelity data. Second, we want to introduce the physics constraints without introducing an underlying non-convex optimization (see the overall design). 

​To achieve both goals, we use the graph isomorphism layer to construct an encoder for nonlinear dimensional reduction. While the graph isomorphism layer enables us to introduce message-passing mechanisms to aggregate information among the finite element nodes, the graph pooling and the multilayer-perceptron enable us to combine the nodal information to complete the graph embedding. This treatment lets us extrapolate the finite element solutions in the latent space (see Figure below).

While this seems like a curve-fitting in a high-dimensional space, the trick to enhance the physics compatibility of the model is to use the solutions generated from the graph auto-encoder to form another Galerkin projection spanned by a very few potential candidate solutions. In other words, instead of assuming that the GNN predicts the finite element solutions, we only assume that the GNN may prediction something quite close. We then leverage this proximity to sample a few snapshots of the response surface to form a temporary space spanned by those candidate solutions. This allows us to solve the Galerkin projection of the balance principle with just the coefficient of the candidate solutions as unknown. Unlike classical reduced order modeling where a linear embedding is used throughout the entire simulations, our new model may generate different Euclidean space at different locations of the parametric space due to the nonlinear embedding afforded by the GNN.  A key benefit of the proposed method is that it does not require searching for the optimal set of parameters in a highly nonlinear landscape (of neural networks). Hence, it does not get stuck in a local minimizer, while it enables the GNN-enabled reduced order simulations to perform with a consistent calculation time. 

Preprint available at ResearchGate [URL]. This paper is Part III of our quest on introducing geometric learning for a variety of computational mechanics problems. The first two parts can be found below. 

1. N. Vlassis, R. Ma", W.C. Sun, Geometric deep learning for computational mechanics Part I: Anisotropic Hyperelasticity, Computer Methods in Applied Mechanics and Engineering, doi:10.1016/j.cma.2020.113299, 2020. [PDF]
2. N.N. Vlassis, W.C. Sun, Geometric deep learning for computational mechanics Part II: Graph embedding for interpretable multi-scale plasticity, Computer Methods in Applied Mechanics and Engineering, doi:10.1016/j.cma.2022.115768, 2023. [Preprint]