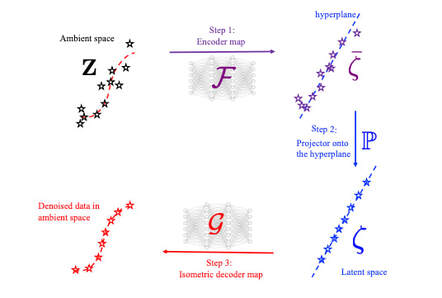
 We (first author = Bahador Bahmani) introduce an isometric manifold embedding data-driven paradigm designed to enable model-free simulations with noisy data sampled from a constitutive manifold. The proposed data-driven approach iterates between a global optimization problem that seeks admissible solutions for the balance principle and a local optimization problem that finds the closest point projection of the Euclidean space that isometrically embeds a nonlinear constitutive manifold. To de-noise the database, a geometric autoencoder is introduced such that the encoder first learns to create an approximated embedding that maps the underlying low-dimensional structure of the high-dimensional constitutive manifold onto a flattened manifold. Unlike conventional auto-encoder where the dimension is reduced by reducing the number of neurons in the downstream layers, we reduce the dimension in a geometric sense through the flattening process. We then obtain the noise-free constitutive responses by projecting data onto a de-noised latent space that is completely flat by assuming that the noise and the underlying constitutive signal are orthogonal to each other, leveraging the conformal mapping between the de-noised latent space and the reconstructed de-manifold. Consequently, a projection from the conservative manifold onto this de-noised constitutive latent space enables us to complete the local optimization step of the data-driven paradigm. Our results show that the isometry constraint may prevent the decoder reintroducing noise. Numerical examples are used to both validate the implementation and demonstrate the accuracy, robustness, and limitations of the proposed paradigm. Preprint available [URL].
0 Comments
Leave a Reply. |
Group NewsNews about Computational Poromechanics lab at Columbia University. Categories
All
Archives
July 2023
|


 RSS Feed
RSS Feed