|
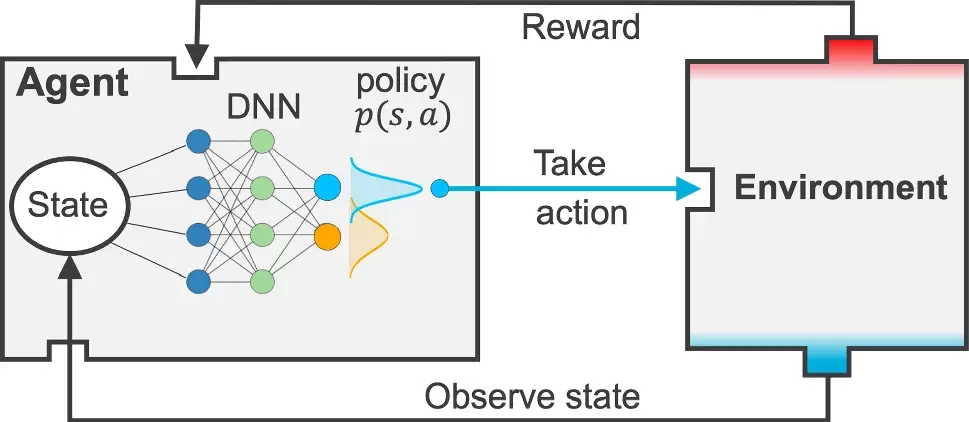
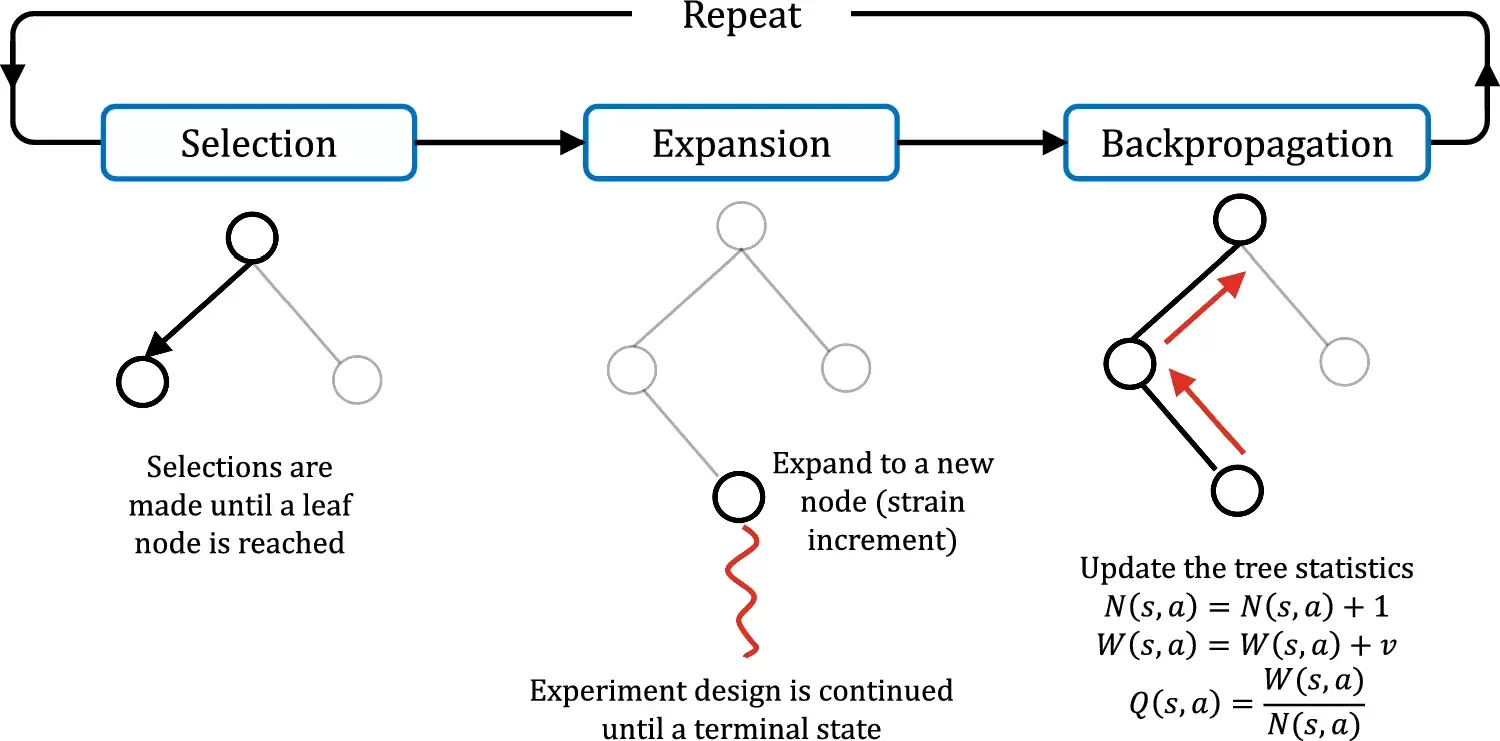
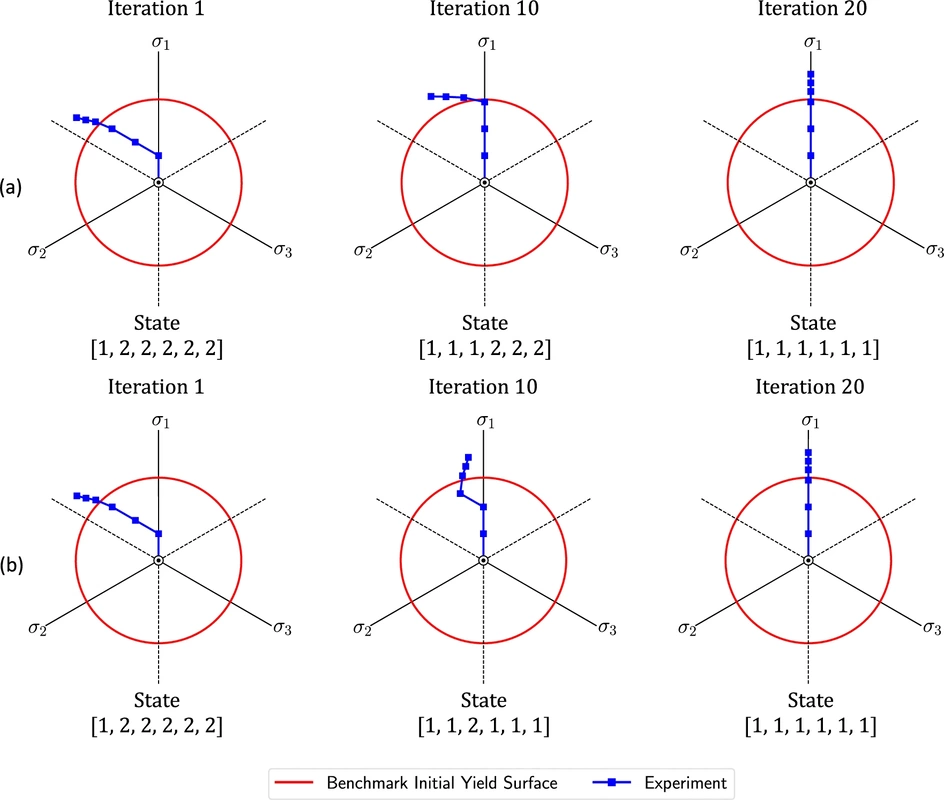
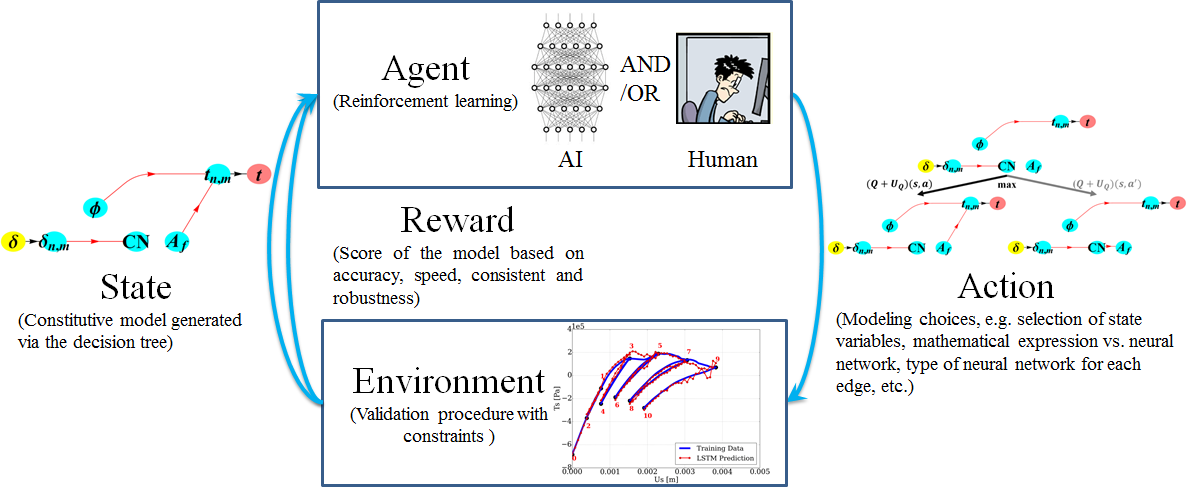
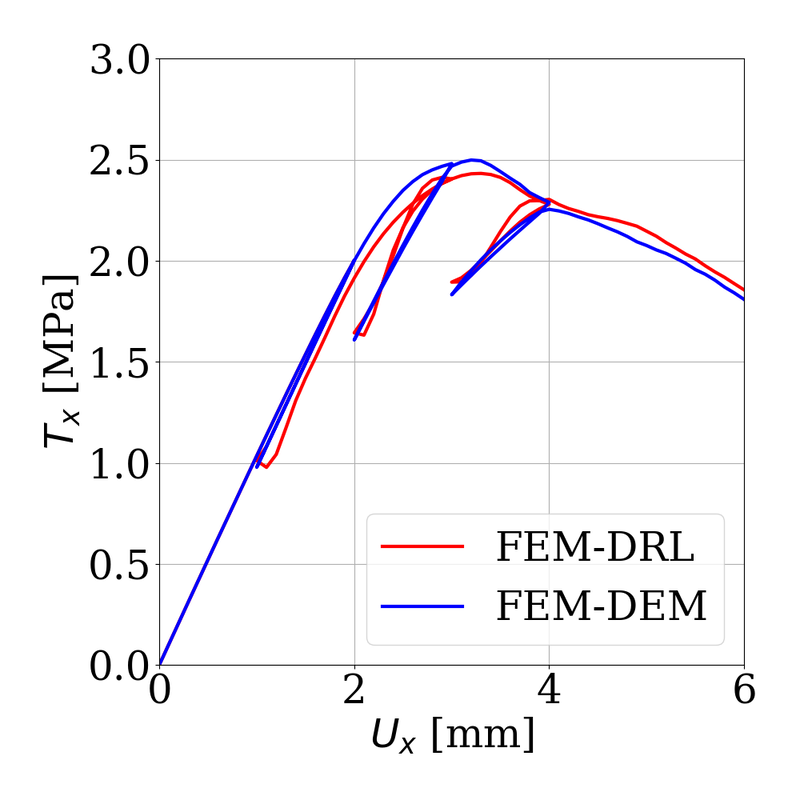
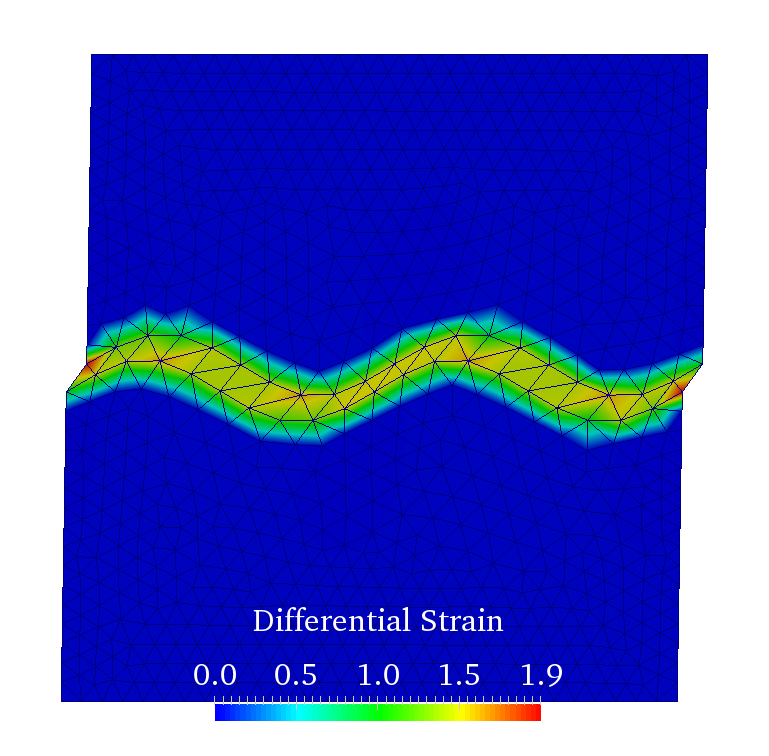
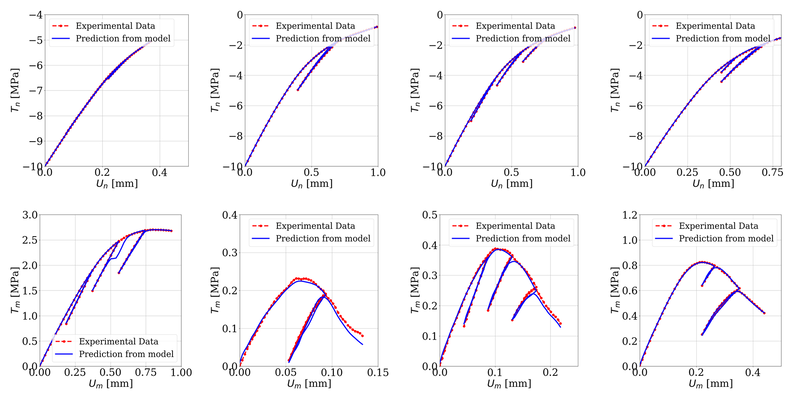
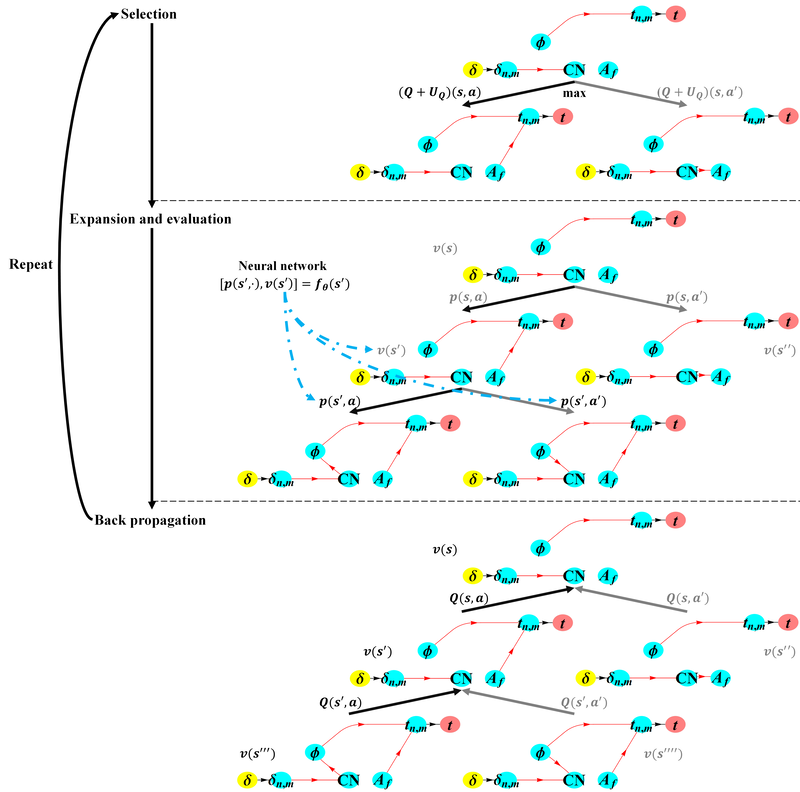
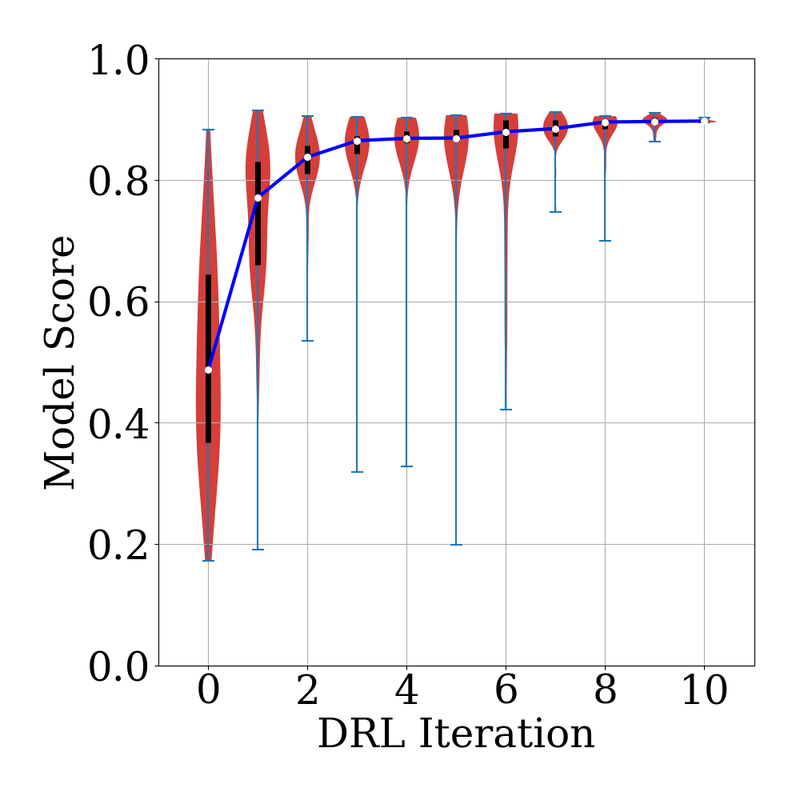
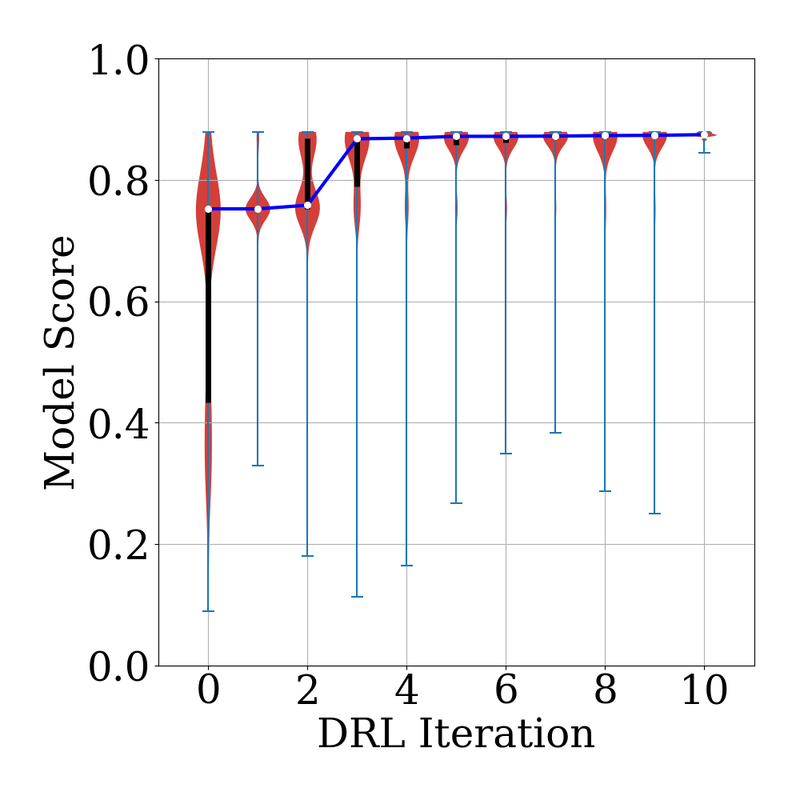
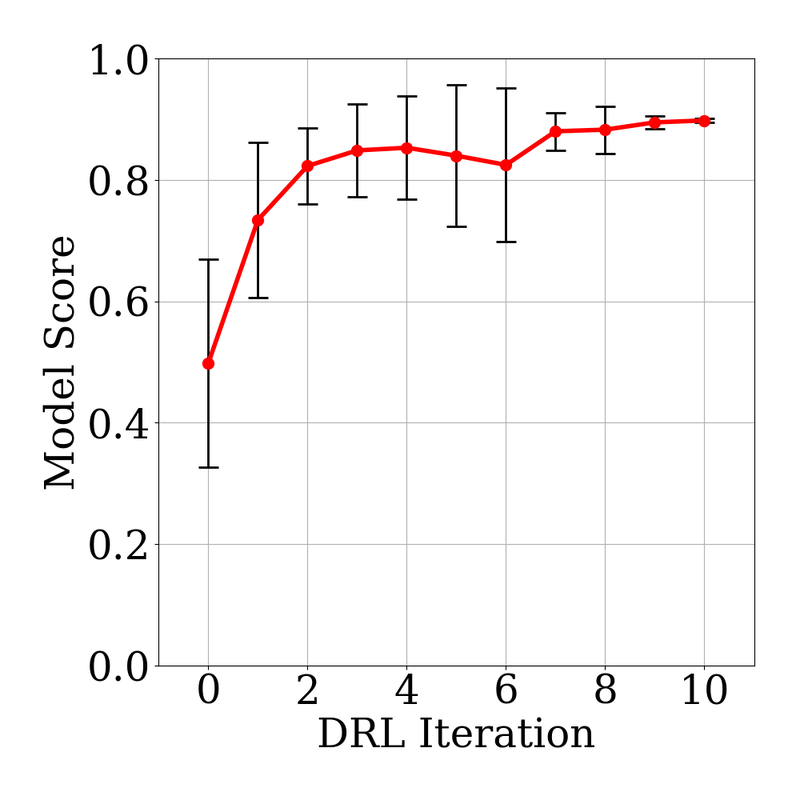
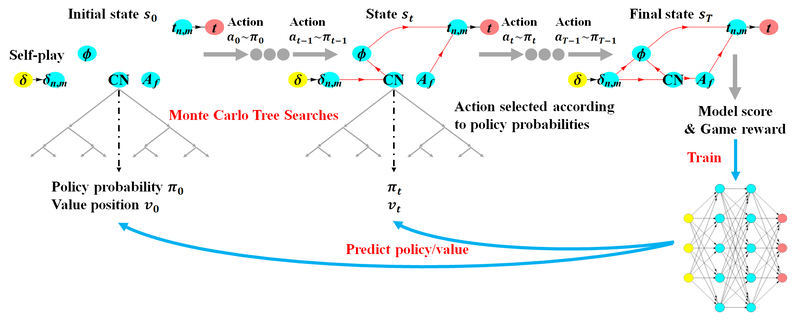
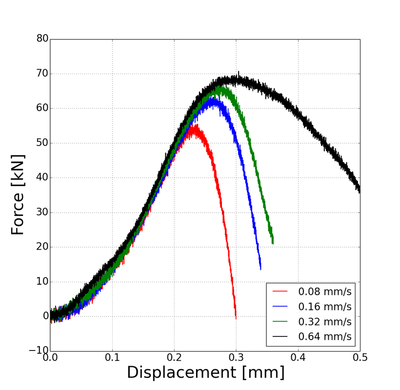
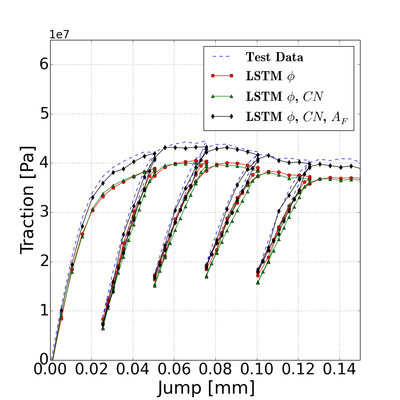
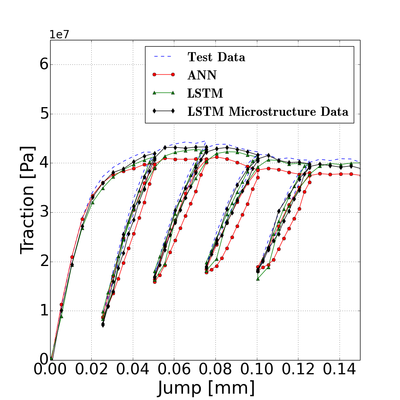
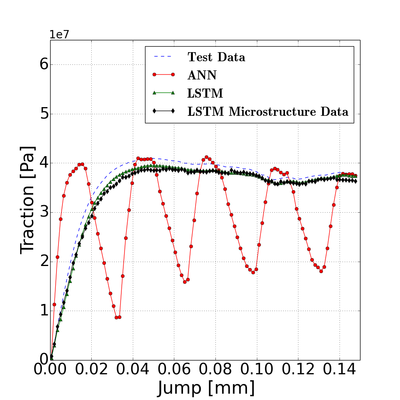
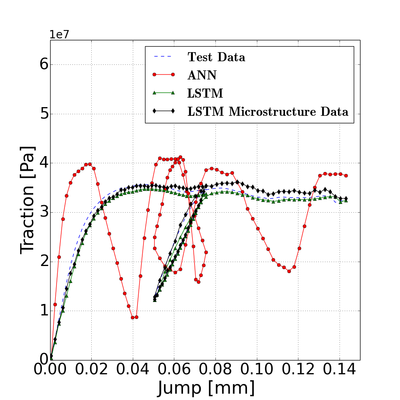
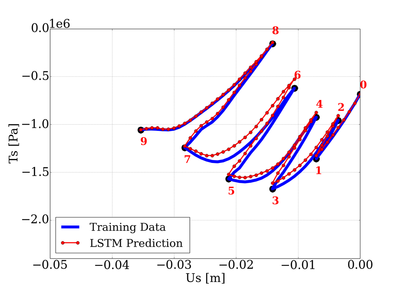
Our collaborative work with Sandia funded by the LDRD project led by Dr. Sharlotte Kramer has just published in the special issue "Machine Learning Theories, Modeling, and Applications to Computational Materials Science, Additive Manufacturing, Mechanics of Materials, Design and Optimization". The article is available in the Computational Mechanics website [URL]. Experimental data are often costly to obtain, which makes it difficult to calibrate complex models. For many models an experimental design that produces the best calibration given a limited experimental budget is not obvious. This paper introduces a deep reinforcement learning (RL) algorithm for design of experiments that maximizes the information gain measured by Kullback–Leibler divergence obtained via the Kalman filter (KF), see figure below. This combination enables experimental design for rapid online experiments where manual trial-and-error is not feasible in the high-dimensional parametric design space. We formulate possible configurations of experiments as a decision tree and a Markov decision process, where a finite choice of actions is available at each incremental step. Once an action is taken, a variety of measurements are used to update the state of the experiment. This new data leads to a Bayesian update of the parameters by the KF, which is used to enhance the state representation. In contrast to the Nash–Sutcliffe efficiency index, which requires additional sampling to test hypotheses for forward predictions, the KF can lower the cost of experiments by directly estimating the values of new data acquired through additional actions. In this work our applications focus on mechanical testing of materials. Numerical experiments with complex, history-dependent models are used to verify the implementation and benchmark the performance of the RL-designed experiments.
0 Comments
An immersed phase field fracture model for microporomechanics with Darcy–Stokes flow
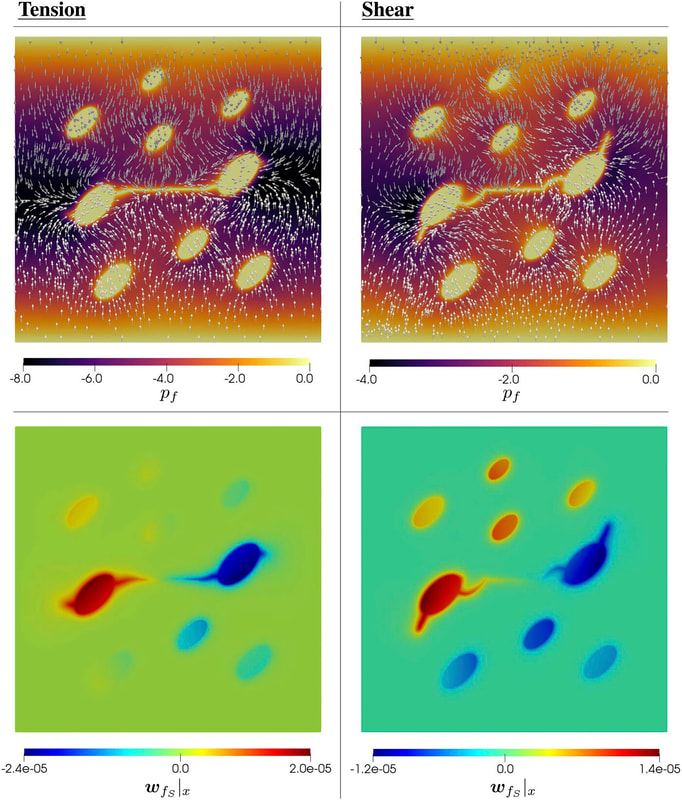
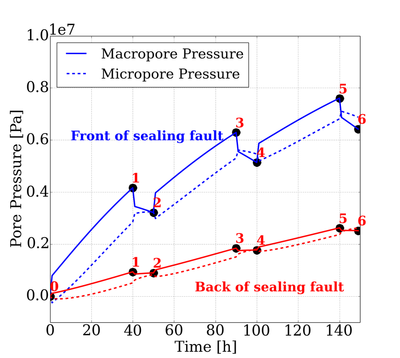
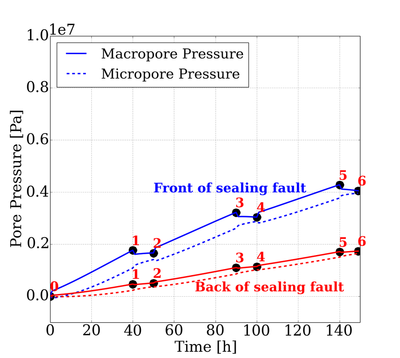
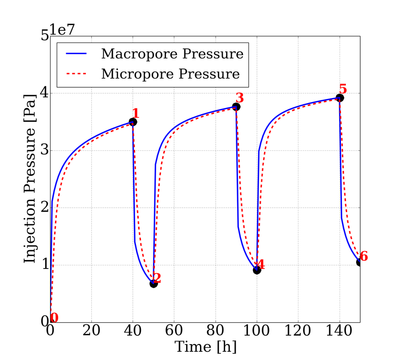
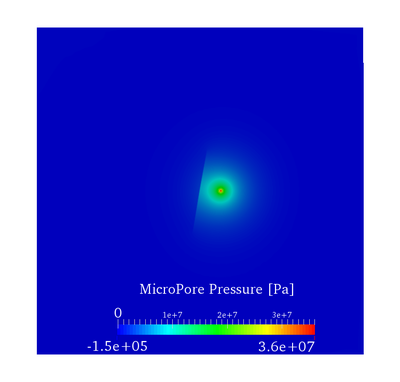
Physics of Fluids 33, 016603 (2021); https://doi.org/10.1063/5.0035602 Hyoung Suk Suh (서형석) and WaiChing Sun (孫維正) ABSTRACT This paper presents an immersed phase field model designed to predict the fracture-induced flow due to brittle fracture in vuggy porous media. Due to the multiscale nature of pores in the vuggy porous material, crack growth may connect previously isolated pores, which leads to flow conduits. This mechanism has important implications for many applications such as disposal of carbon dioxide and radioactive materials and hydraulic fracture and mining. To understand the detailed microporomechanics that causes the fracture-induced flow, we introduce a new phase field fracture framework where the phase field is not only used as an indicator function for damage of the solid skeleton but also used as an indicator of the pore space. By coupling the Stokes equation that governs the fluid transport in the voids, cavities, and cracks and Darcy’s flow in the deformable porous media, our proposed model enables us to capture the fluid–solid interaction of the pore fluid and solid constituents during crack growth. Numerical experiments are conducted to analyze how the presence of cavities affects the accuracy of predictions based on the homogenized effective medium during crack growth. Author: Nikolas Vlassis, WaiChing Sun
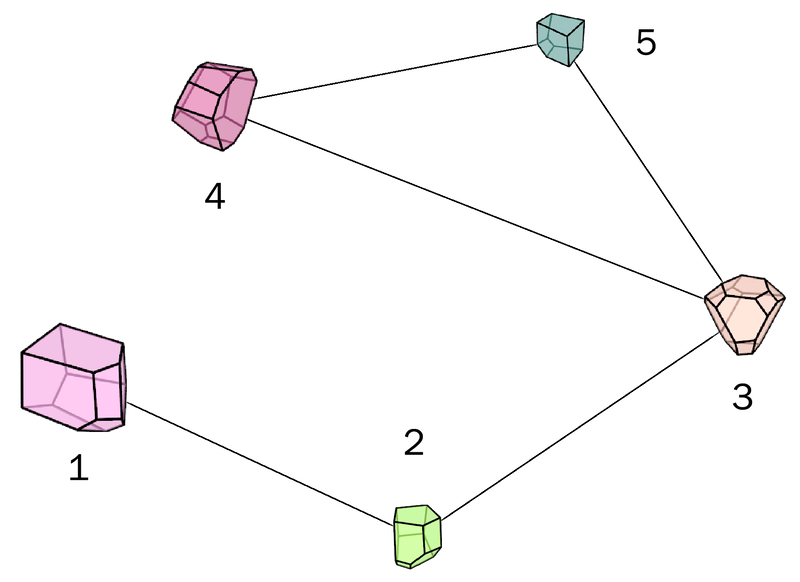
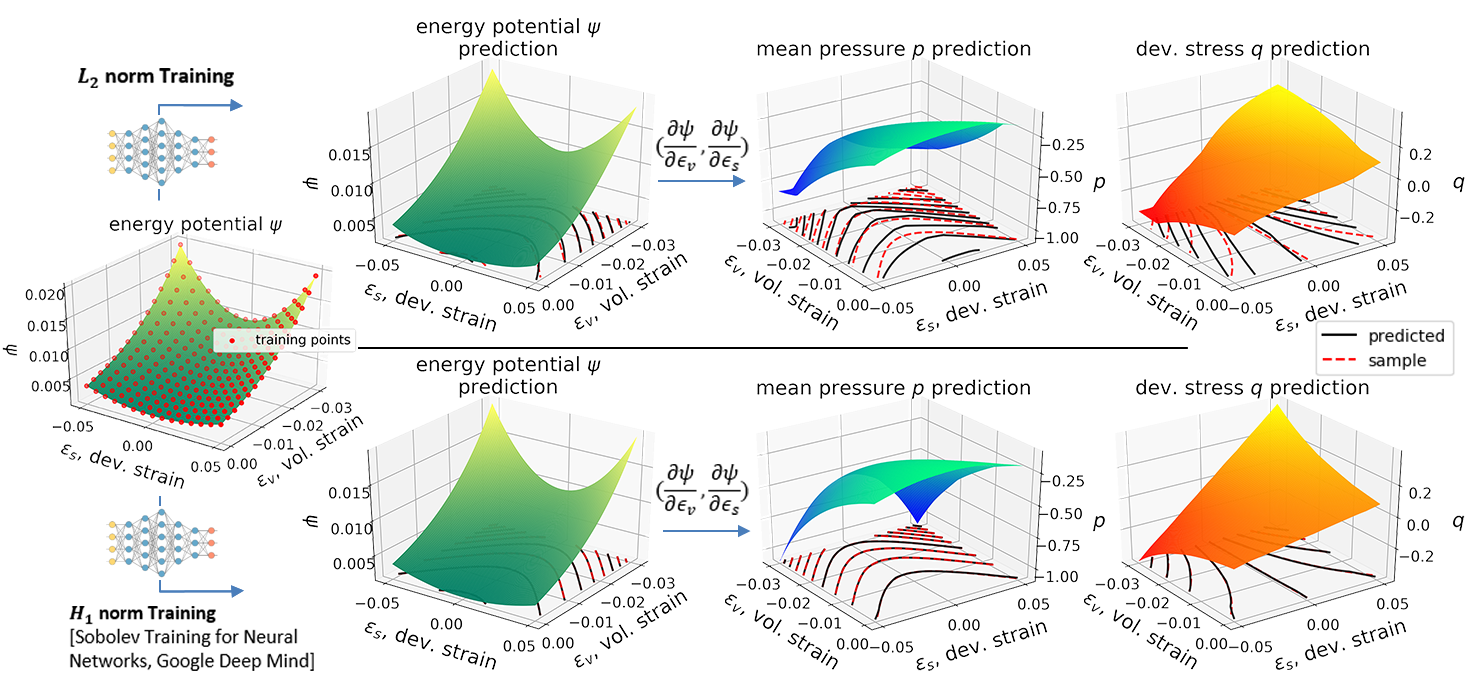
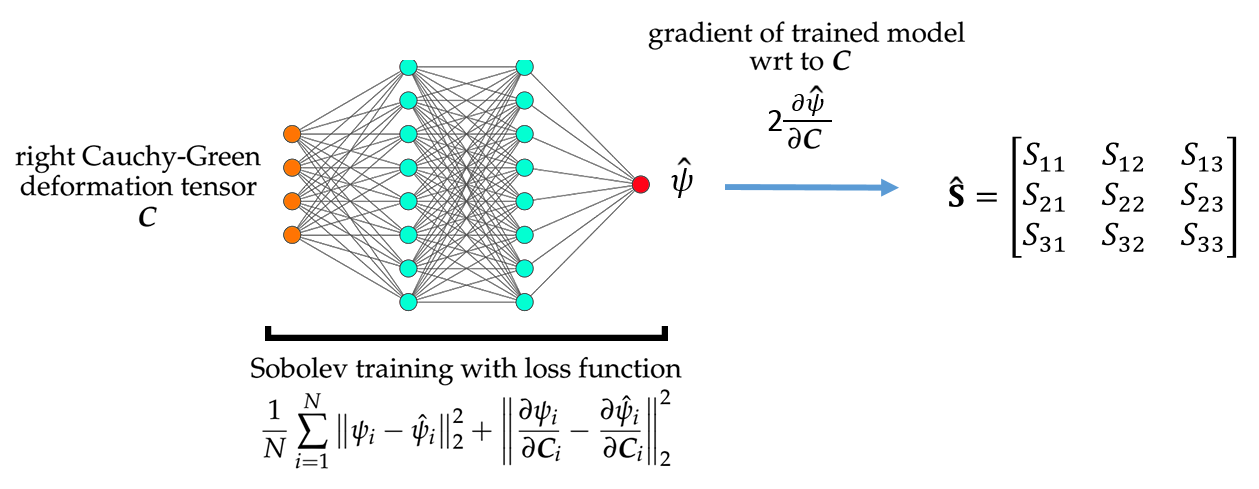
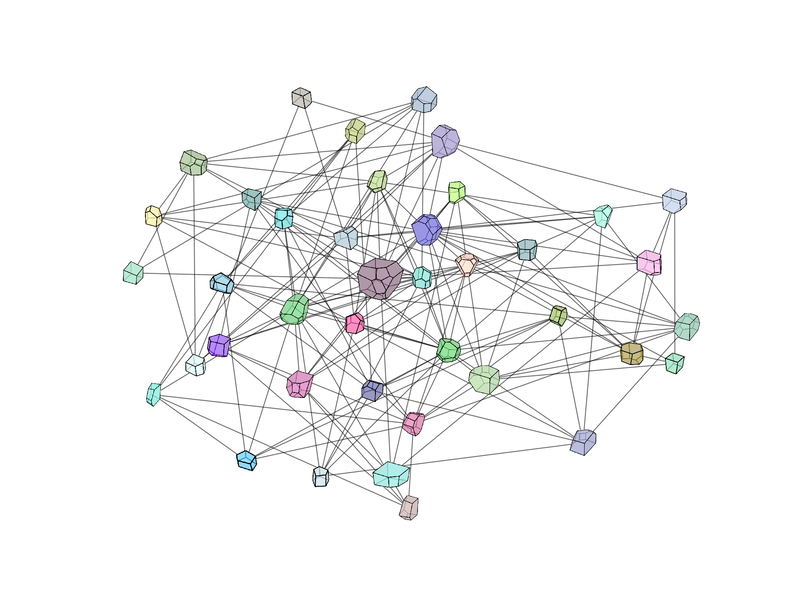
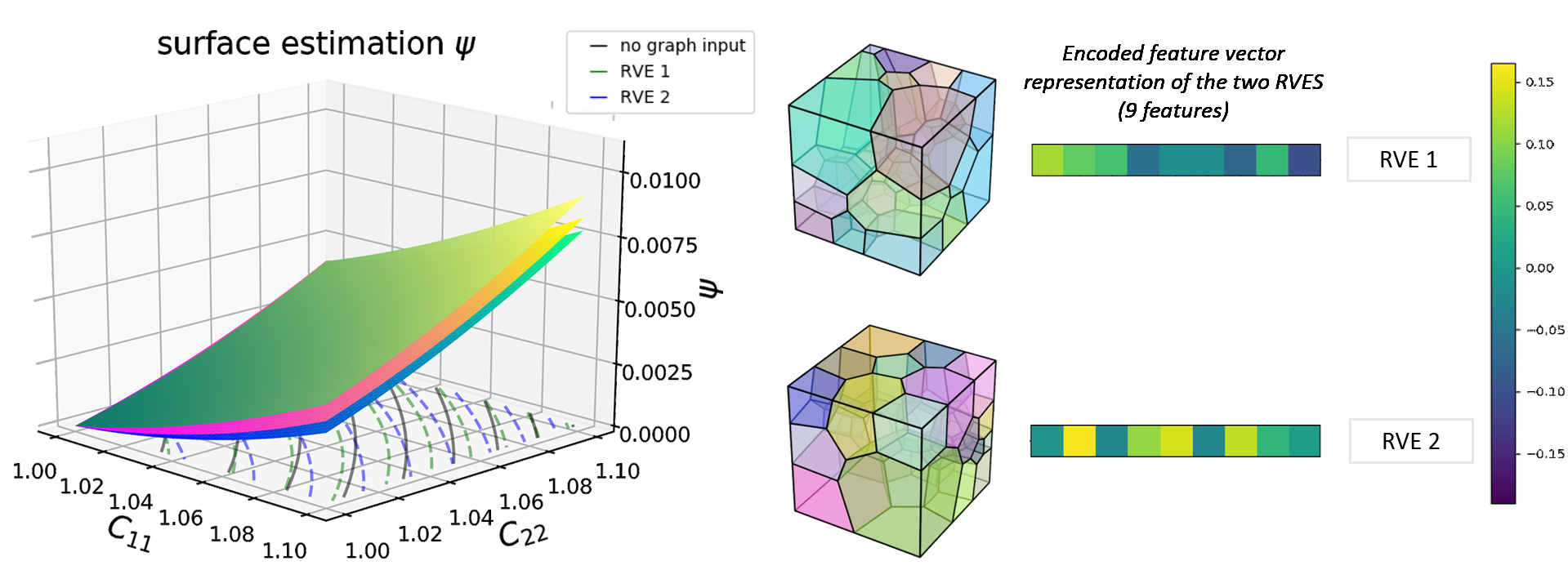
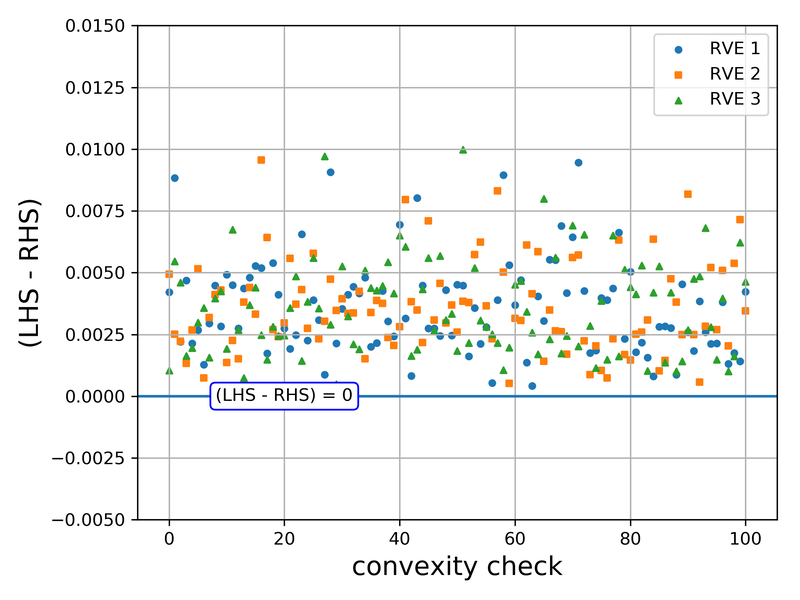
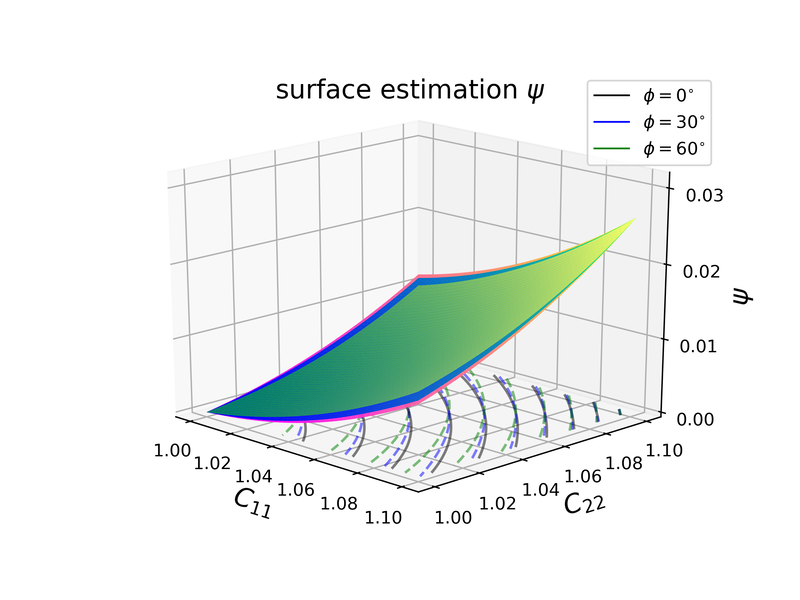
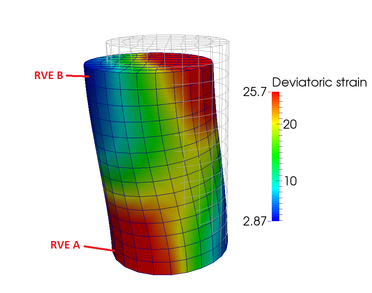
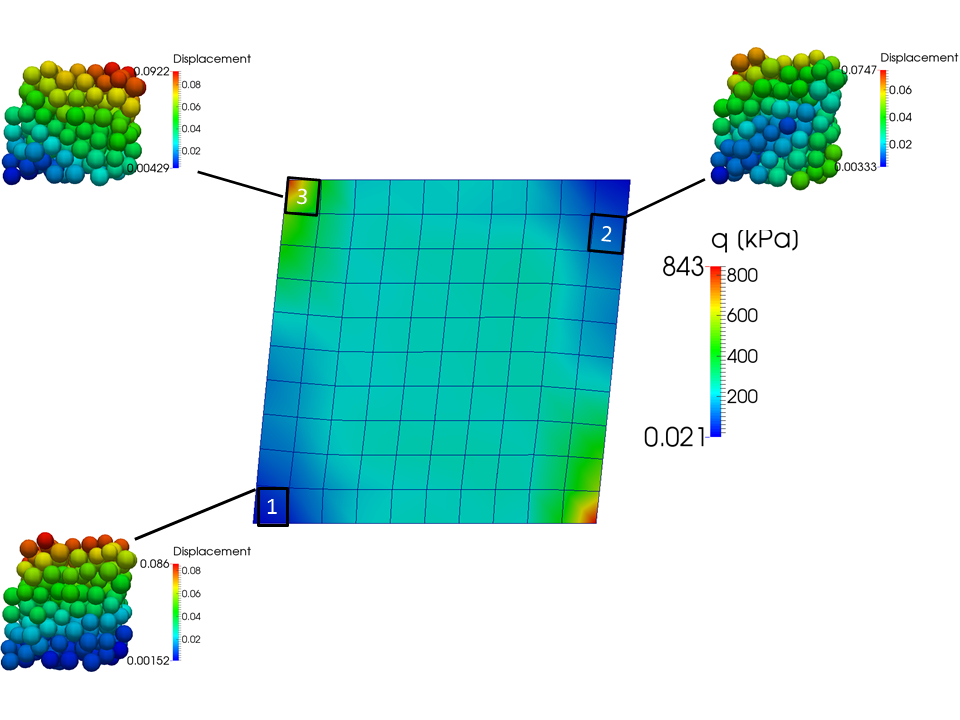
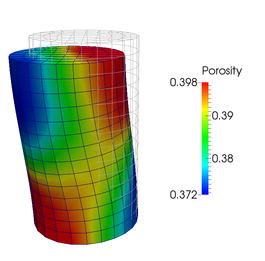
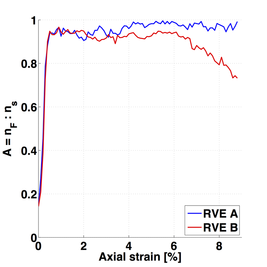
Abstract: We present a machine learning approach that integrates geometric deep learning and Sobolev training to generate a family of finite strain anisotropic hyperelastic models that predict the homogenized responses of polycrystals previously unseen during the training. While hand-crafted hyperelasticity models often incorporate homogenized measures of microstructural attributes, such as the porosity or the averaged orientation of constitutes, these measures may not adequately reflect the topological structures of the attributes. We fill this knowledge gap by introducing the concept of the weighted graph as a new high-dimensional descriptor that represents topological information, such as the connectivity of anisotropic grains in an assemble. By leveraging a graph convolutional deep neural network in a hybrid machine learning architecture previously used in Frankel et al. 2019, the artificial intelligence extracts low-dimensional features from the weighted graphs and subsequently learns the influence of these low-dimensional features on the resultant stored elastic energy functionals. To ensure smoothness and prevent unintentionally generating a non-convex stored energy functional, we adopt the Sobolev training method for neural networks such that a stress measure is obtained implicitly by taking directional derivatives of the trained energy functional. Results from numerical experiments suggest that Sobolev training is capable of generating a hyperelastic energy functional that predicts both the elastic energy and stress measures more accurately than the classical training that minimizes L2 norm. Verification exercises against unseen benchmark FFT simulations and phase-field fracture simulations using the geometric learning generated elastic energy functional are conducted to demonstrate the quality of the predictions. [manuscript] We present a new thermal-mechanical-chemical-phase field model that captures the multi-physical coupling effects of precipitation creeping, crystal plasticity, anisotropic fracture, and crack healing in polycrystalline rock at various temperature and strain-rate regimes. This model is solved via a fast Fourier transfer solver with an operator-split algorithm to update displacement, temperature and phase field, and chemical concentration incrementally. In nuclear waste disposal in salt formation, brine inside the crystal salt may migrate along the grain boundary and cracks due to the gradient of interfacial energy and pressure. This migration has a significant implication on the permeability evolution, creep deformation, and crack healing within rock salt but is difficult to incorporate implicitly via effective medium theories compared with computational homogenization. As such, we introduce a thermodynamic framework and a corresponding computational implementation that explicitly captures the brine diffusion along the grain boundary and crack at the grain scale. Meanwhile, the anisotropic fracture and healing are captured via a high-order phase field that represents the regularized crack region in which a newly derived non-monotonic driving force is used to capture the fracture and healing due to the solution precipitation. Numerical examples are presented to demonstrate the capacity of the thermodynamic framework to capture the multiphysics material behaviors of rock salt. This paper is Part II of our work on modeling polycrystal salt for nuclear waste disposal. Reference
One key drawback of classical discrete/distinct/granular element methods for particulate mechanics is that they cannot generate any kinetic and kinematics information at the sub-grain scales. Nevertheless, many dissipative mechanisms of granular materials are actually originated from path-dependent behaviors at the sub-grain scales where wear, damage, fracture and fragmentation occurs. This simplification therefore may lead to a departure of force chain topology and therefore make the resultant simulations inaccurate. Recovery of these sub-scale information while capturing the geometry and form of each individual grains is inherently a difficult task.
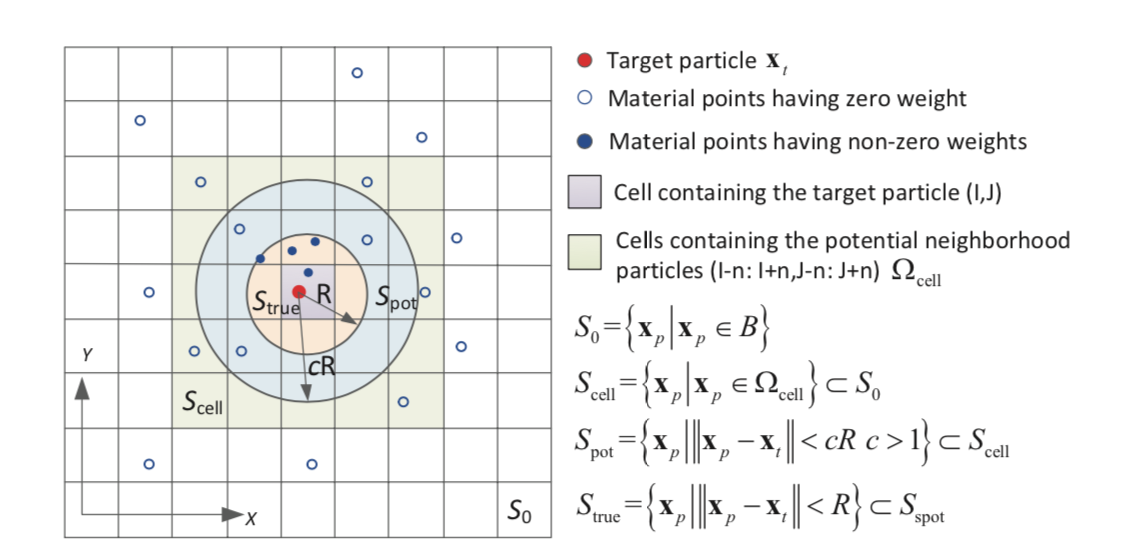
In this work, our postdoc Dr. Chuanqi Liu introduces an implicit material point method designed to bypass meshing of bodies by employing level set functions to represent boundaries at structured grids. This implicit function representation provides an elegant means to link an unbiased intermediate reference surface with the true boundaries by closest point projection as shown Leichner et al. 2019. We then enforce the contact constraints by a penalty method where the Coulomb friction law is implemented as an elastoplastic constitutive model such that a return mapping algorithm can be used to provide constitutive updates for both the stick and slip states. To evolve the geometry of the contacts properly, the Hamilton-Jacobi equation is solved incrementally such that the level set and material points are both updated according to the deformation field. To improve the accuracy and regularity of the numerical integration of the material point method, a moving least square method is used to project numerical values of the material points back to the standard locations for Gaussian-Legendre quadrature. Several benchmarks are used to verify the proposed model. Comparisons with discrete element simulations are made to analyze the importance of stress fields on predicting the macroscopic responses of granular assemblies. [manuscript] Abstract: This paper presents the application of a fast Fourier transform (FFT) based method to solve two phase field models designed to simulate crack growth of strongly anisotropic materials in the brittle regime. By leveraging the ability of the FFT-based solver to generate solutions with global continuities, we design two simple algorithms to capture the complex fracture patterns (e.g. sawtooth, and curved crack growth) common in materials with strongly anisotropic surface energy via the multi-phase-field and high-order phase-field frameworks. A staggered operator-split solver is used where both the balance of linear momentum and the phase field governing equations are formulated in the periodic domain. The unit phase field of the initial failure region is prescribed by the penalty method to alleviate the sharp material contrast between the initial failure region and the base material. The discrete frequency vectors are generalized to estimate the second and fourth order gradients such that the Gibbs effect near shape interfaces or jump conditions can be suppressed. Furthermore, a pre-conditioner is adopted to improve the convergence rate of the iterative linear solver. Three numerical experiments are used to systematically compare the performance of the FFT-based method in the multi-phase-field and high-order phase-field frameworks. [PDF] A phase field framework for capillary-induced fracture in unsaturated porous media: drying-induced vs. hydraulic cracking Abstract: This article introduces a unified mathematical framework to replicate both desiccation-induced and hydraulic fracturing in low-permeable unsaturated porous materials observed in experiments. The unsaturated porous medium is considered as a three-phase solid-liquid-gas effective medium of which each constituent occupies a fraction of the representative elementary volume. As such, an energy-minimization-based phase-field model (PFM) is formulated along with the Biot's poroelasticity theory to replicate the sub-critical crack growth in the brittle regime. Unlike hydraulic fracturing where the excess pore liquid pressure plays an important role at the onset and propagation of cracks, desiccation cracks are mainly driven by deformation induced by water retention. Therefore, the wettability of the solid skeleton may affect the evolution of the capillary pressure (suction) and change the path-dependent responses of the porous media. This air-water-solid interaction may either hinder or enhance the cracking occurrence. This difference of capillary effect on crack growth during wetting and drying is replicated by introducing retention-sensitive degradation mechanisms in our phase field fracture approach. To replicate the hydraulic behaviors of the pore space inside the host matrix and that of the cracks, the path-dependent changes of the intrinsic permeability due to crack growth and porosity changes are introduced to model the flow conduit in open and closed cracks. Numerical examples of drying-induced and hydraulic fracturing demonstrate the capability of the proposed model to capture different fracture patterns, which qualitatively agrees with the fracture mechanisms of related experiments documented in the literature. [PDF] A configurational force for adaptive re-meshing of gradient-enhanced poromechanics problems with history-dependent variables SeonHong Na, Eric C Bryant, Waiching Sun We introduce a mesh-adaption framework that employs a multi-physical configurational force and Lie algebra to capture multi-physical responses of fluid-infiltrating geological materials while maintaining the efficiency of the computational models. To resolve sharp changes of both displacement and pore pressure, we introduce an energy-estimate-free re-meshing criterion by extending the configurational force theory to consider the energy dissipation due to the fluid diffusion and the gradient-dependent plastic flow. To establish new equilibria after re-meshing, the local tensorial history-dependent variables at the integration points are first decomposed into spectral forms. Then, the principal value and direction are projected onto a smooth field interpolated by the basis function of the finite element space via the Lie-algebra mapping. Our numerical results indicate that this Lie algebra operator, in general, leads to a new trial state closer to the equilibrium than the ones obtained from the tensor component mapping approach. A new configurational force for dissipative fluid-infiltrating porous materials that exhibit gradient-dependent plastic flow is introduced such that the re-meshing may accommodate the need to resolve the sharp pressure gradient as well as the strain localization. The predicted responses are found to be not influenced by the mesh size due to the micromorphic regularization, while the adaptive meshing enables us to capture the width of deformation bands without the necessity of employing fine mesh everywhere in the domain. [PDF] Abstract:
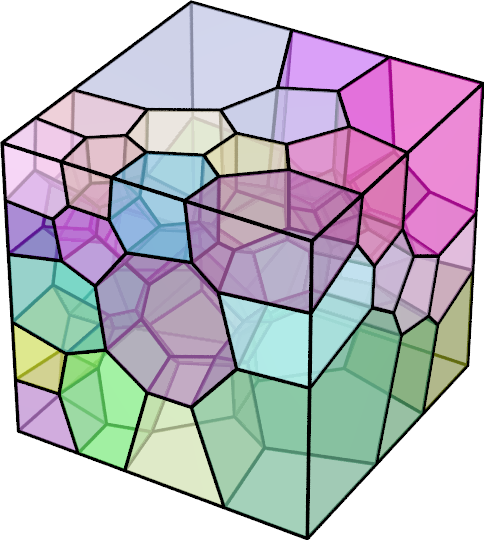
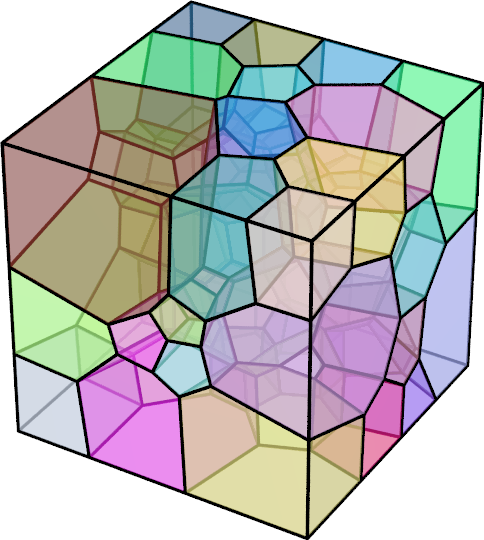
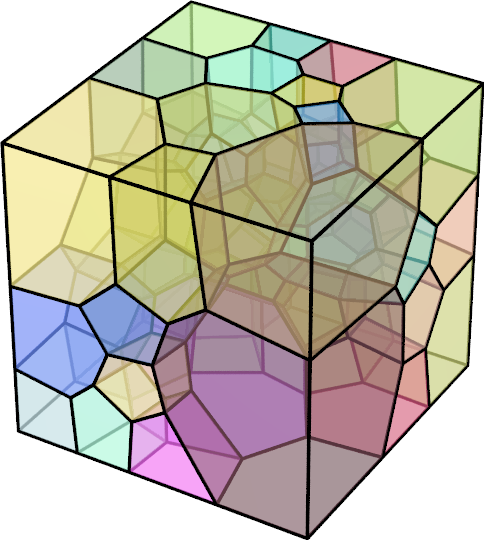
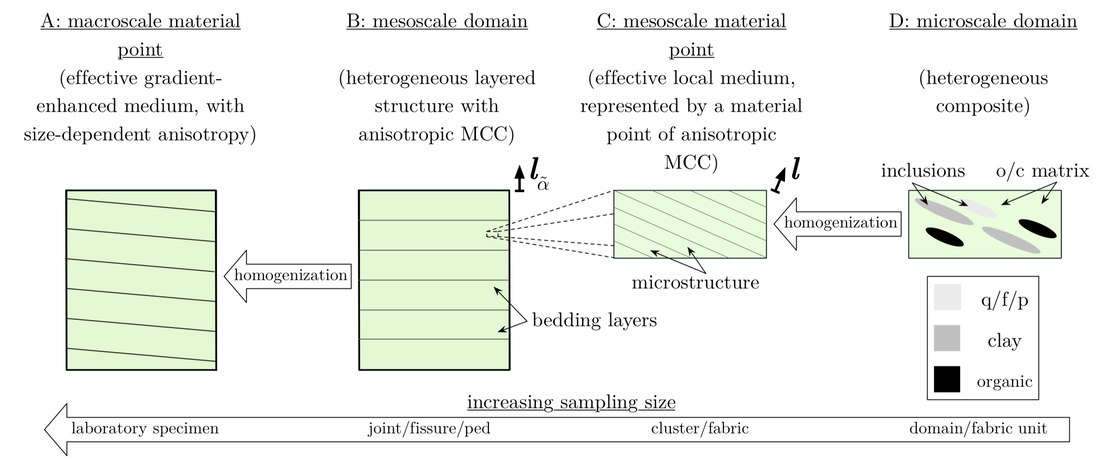
We introduce a regularized anisotropic modified Cam-clay (MCC) model which captures the size-dependent anisotropic elastoplastic responses for clay, mudstone, shales, and sedimentary rock. By homogenizing the multiscale anisotropic effects induced by clay particle aggregate, clusters, peds, micro-fabric, and mineral contact across length scales, we introduce two distinctive anisotropic mechanisms for the MCC model at the material point and mesoscale levels. We first employ a mapping that links the anisotropic stress state to a fictitious isotropic principal stress-space to introduce anisotropy at the material point scale. Then, the mesoscale anisotropy is introduced via an anisotropic regularization mechanism. This anisotropic regularization mechanism is triggered by introducing gradient-dependence of the internal variables through a penalty method such that the resultant gradient-enhanced plastic flow may exhibit anisotropic responses non-coaxial to the stress gradient of the yield function. The influence of the size-dependent anisotropy on the formation of the shear band and the macroscopic responses of the effective media are analyzed in 2D and 3D numerical examples. [PDF] Abstract:
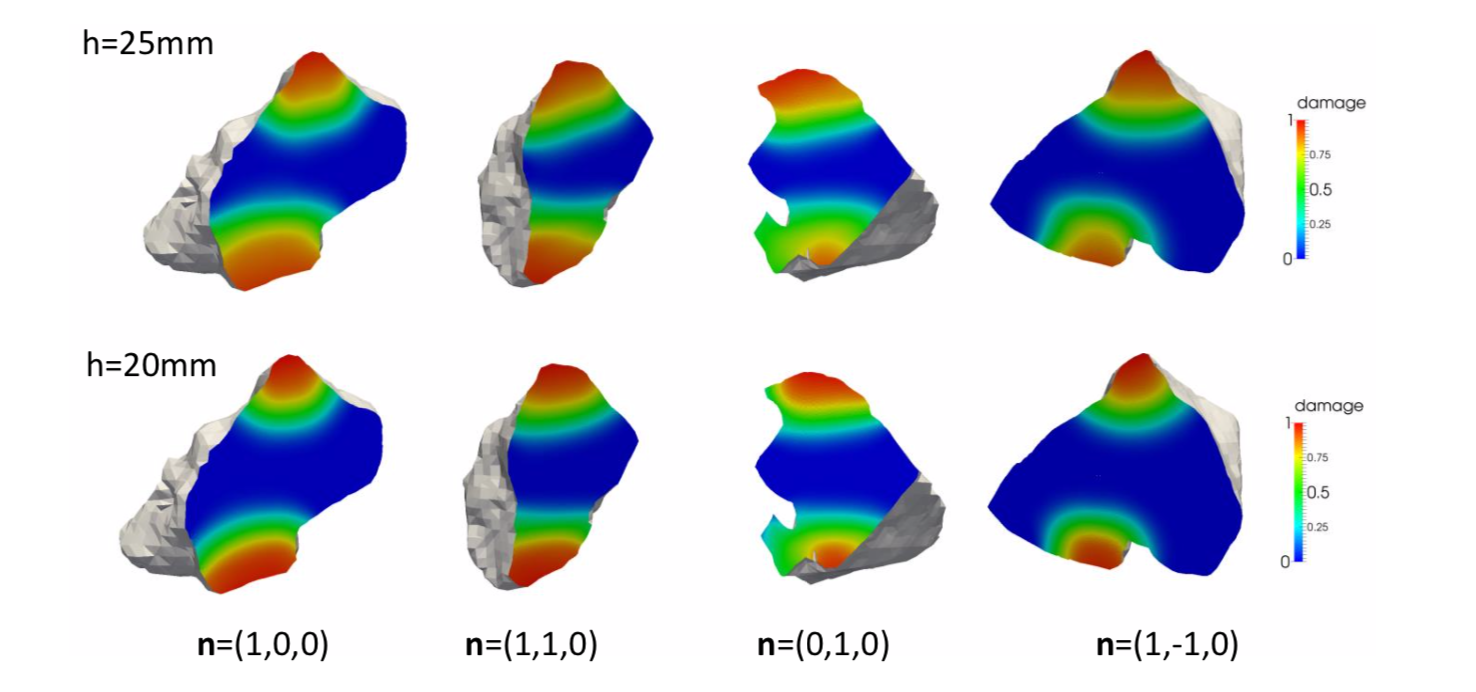
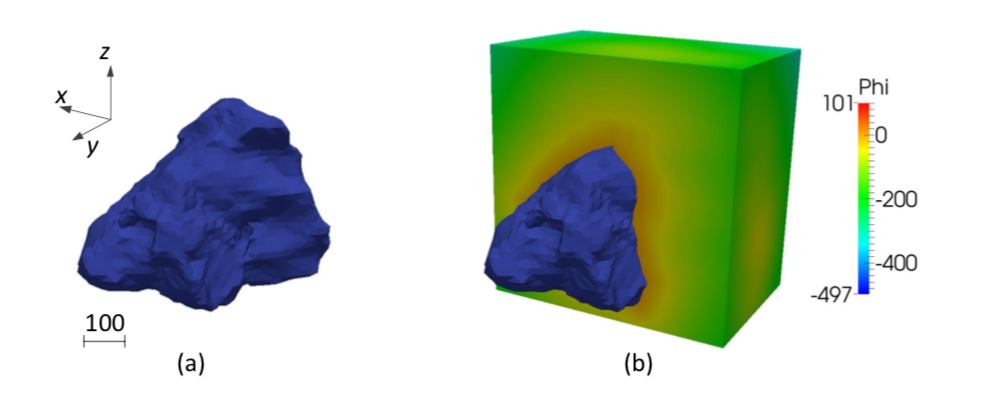
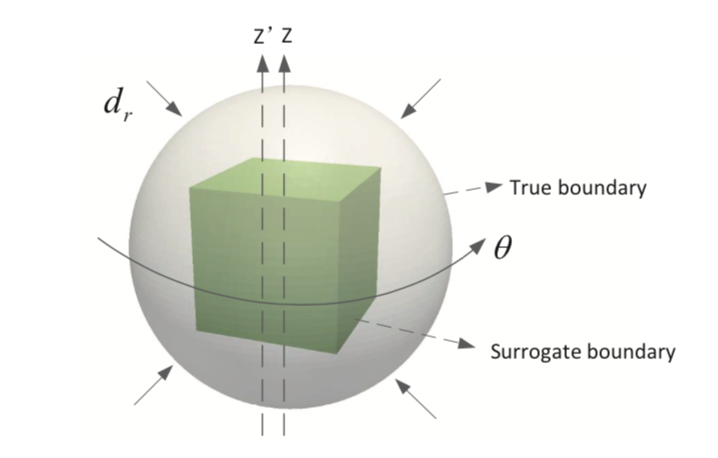
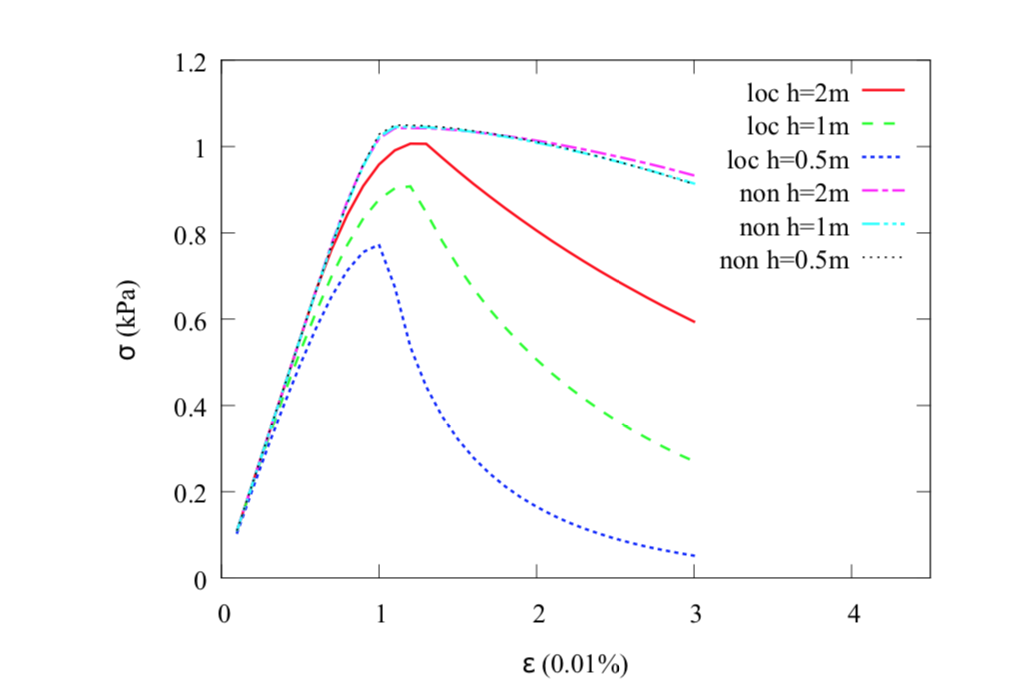
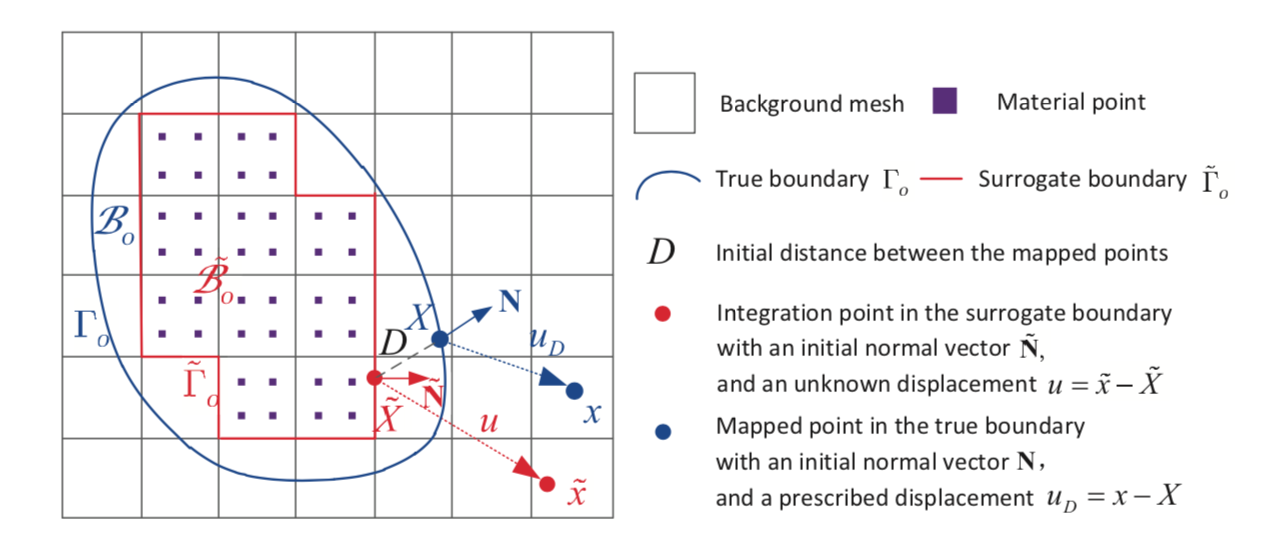
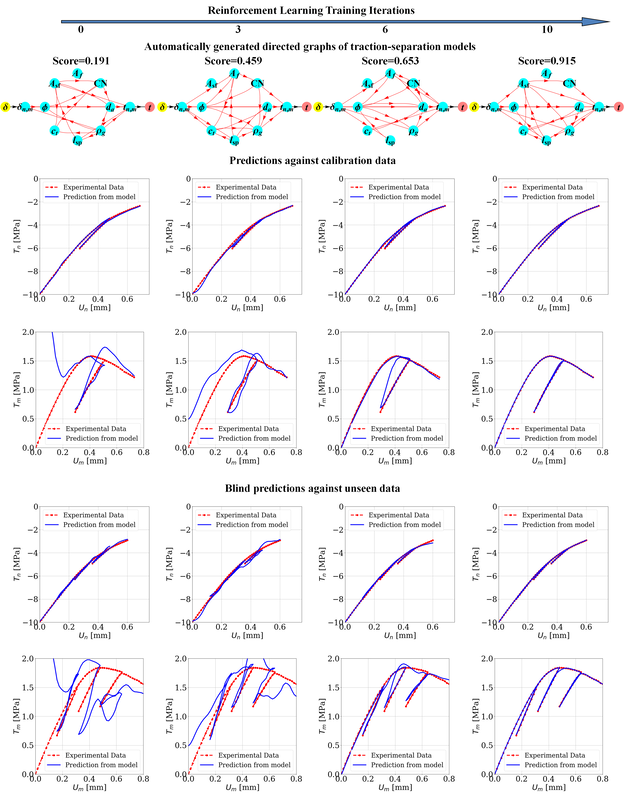
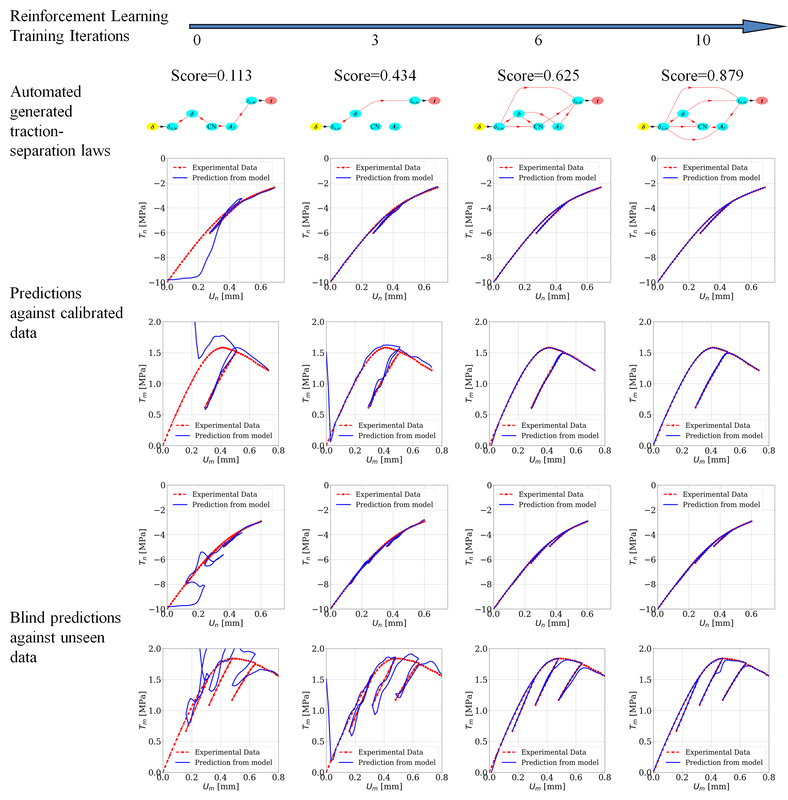
We introduce a mathematical framework designed to enable a simple image-to-simulation workflow for solids of complex geometries in the geometrically nonlinear regime. While the material point method is used to circumvent the mesh distortion issues commonly exhibited in Lagrangian meshes, a shifted domain technique originated from [Main and Scovazzi, 2018a,b] is used to represent the boundary conditions implicitly via a level set or signed distance function. Consequently, this method completely bypasses the need to generate high-quality conformal mesh to represent complex geometries and therefore allows modelers to select the space of the interpolation function without the constraints due to the geometrical need. This important simplification enables us to simulate deformation of complex geometries inferred from voxel images. Verification examples on deformable body subjected to finite rotation have shown that the new shifted domain material point method is able to generate frame-indifferent results. Meanwhile, simulations using microCT images of a Hostun sand have demonstrated that this method is able to reproduce the quasi-brittle damage mechanisms of single grain without the excessively concentrated nodes commonly displayed in conformal meshes that represent 3D objects with local fine details. [PDF] Our first article on automated meta-modeling of path-dependent materials accepted in CMAME12/7/2018 In this work, we introduce a single-player game in which we attempt to use the formation of directed graph to represent the thought process / decision process of writing a cohesive zone model. In this work, the AI uses deep reinforcement learning to form knowledge of mechanics represented by directed graph, this knowledge is then used to generate constitutive law. Unlike previous supervised learning method, the automatically discovered/generated/implemented cohesive zone model is robust, accuracy and interpretable by human. Full details can be from the article [URL]. The second one will be coming soon.
Our work on mixed-mode phase field fracture with consistent kinematics has just published in CMAME9/25/2018 A mixed-mode phase field fracture model in anisotropic rocks with consistent kinematics Eric Bryant & WaiChing Sun Under a pure tensile loading, cracks in brittle, isotropic, and homogeneous materials often propagate such that pure mode I kinematics are maintained at the crack tip. However, experiments performed on geo-materials, such as sedimentary rock, shale, mudstone, concrete and gypsum, often lead to the conclusion that the mode I and mode II critical fracture energies/surface energy release rates are distinctive. This distinction has great influence on the formation and propagation of wing cracks and secondary cracks from pre-existing flaws under a combination of shear and tensile or shear and compressive loadings. To capture the mixed-mode fracture propagation, a mixed-mode I/II fracture model that employs multiple critical energy release rates based on Shen and Stephansson, IJRMMS, 1993 is reformulated in a regularized phase field fracture framework. We obtain the mixed-mode driving force of the damage phase field by balancing the microforce. Meanwhile, the crack propagation direction and the corresponding kinematics modes are determined via a local fracture dissipation maximization problem. Several numerical examples that demonstrate mode II and mixed-mode crack propagation in brittle materials are presented. Possible extensions of the model capturing degradation related to shear/compressive damage, as commonly observed in sub-surface applications and triaxial compression tests, are also discussed. [URL] Our manuscript on using recurrent neural network to perform offline homogenization for multi-phase multi-permeability porous media has been accepted by CMAME today. This technique break down the computational barrier commonly exhibited in DEM-FEM and FEM2 models and therefore allow simulations connected across multiple scales. Spectral decomposition is used to correct the frame-dependent issues exhibited in RNN constitutive laws; issues on over- and under-fitting are regularized; k-fold validation techniques are used; and a model selection procedure on a directed graph is introduced. [PDF]
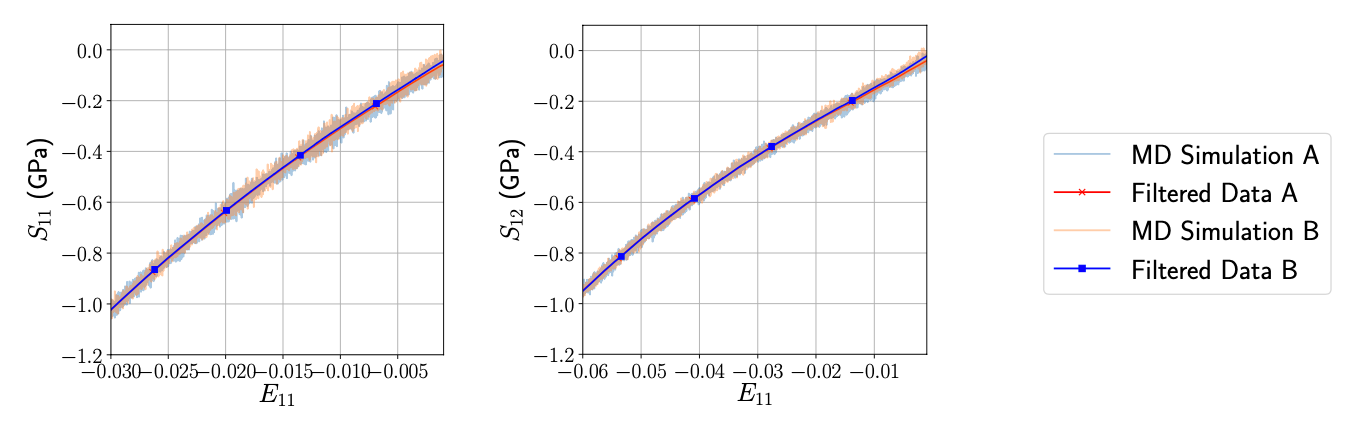
Computational thermomechanics of crystalline rock. Part I: a combined multi-phase-field/crystal plasticity approach for single crystal simulations SeonHong Na, WaiChing Sun Abstract: Rock salt is one of the major materials used for nuclear waste geological disposal. The desired characteristics of rock salt, i.e., high thermal conductivity, low permeability, and self-healing are highly related to its crystalline microstructure. Conventionally, this microstructural effect is often incorporated phenomenologically in macroscopic damage models. Nevertheless, the thermomechanical behavior of a crystalline material is dictated by the nature of crystal lattice and micromechanics (i.e., the slip-system). This paper presents a model proposed to examine these fundamental mechanisms at the grain scale level. We employ a crystal plasticity framework in which single-crystal halite is modeled as a face-centered cubic (FCC) structure with the secondary atoms in its octahedral holes, where a pair of Na+ and Cl− ions forms the bond basis. Utilizing the crystal plasticity framework, we capture the existence of an elastic region in the stress space and the sequence of slip system activation of single-crystal halite under different temperature ranges. To capture the anisotropic nature of the intragranular fracture, we couple a crystal plasticity model with a multi-phase-field simulation that does not require high-order terms for the phase field. Numerical examples demonstrate that the proposed model is able to capture the anisotropy of inelastic and damage behavior under various loading rates and temperature conditions. [PDF] Title:
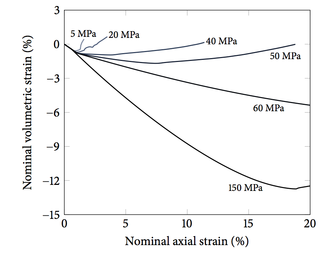
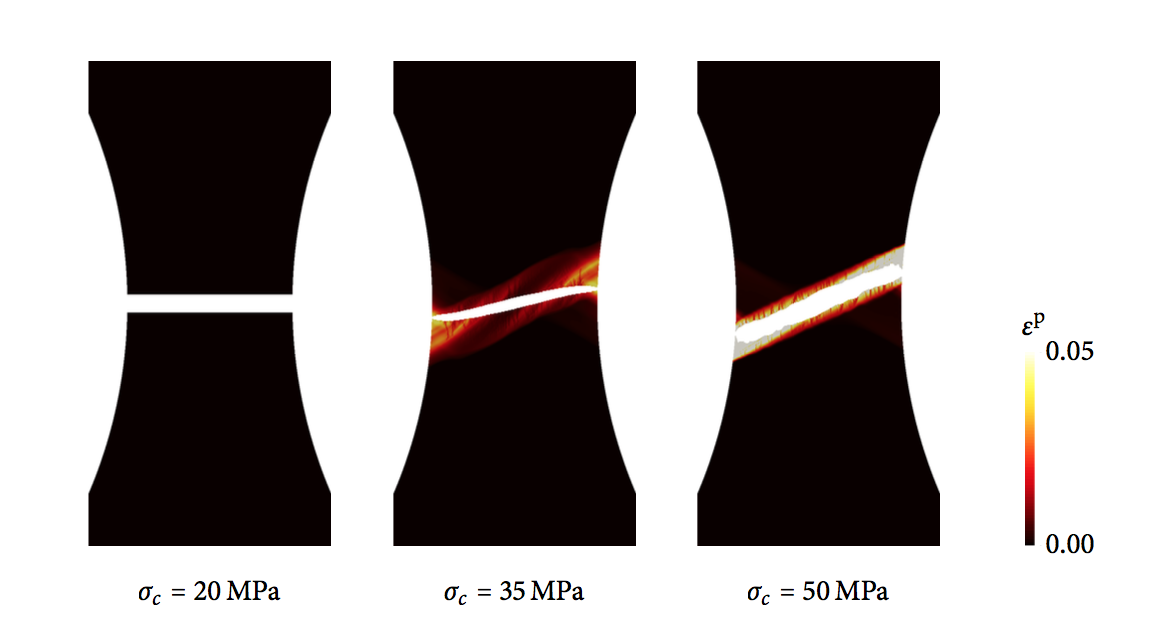
Coupled phase-field and plasticity modeling of geological materials: from brittle fracture to ductile flow Author: Jinhyun Choo, WaiChing Sun Accepted Date: Oct 4th, 2017 Abstract: The failure behavior of geological materials depends heavily on confining pressure and strain rate. Under a relatively low confining pressure, these materials tend to fail by brittle, localized fracture, but as the confining pressure increases, they show a growing propensity for ductile, diffuse failure accompanying plastic flow. Furthermore, the rate of deformation often exerts control on the brittleness. Here we develop a theoretical and computational modeling framework that encapsulates this variety of failure modes and their brittle-ductile transition. e framework couples a pressure-sensitive plasticity model with a phase-field approach to fracture which can simulate complex fracture propagation without tracking its geometry. We derive a phase-field formulation for fracture in elastic-plastic materials as a balance law of microforce, in a new way that honors the dissipative nature of the fracturing processes. For physically meaningful and numerically robust incorporation of plasticity into the phase-field model, we introduce several new ideas including the use of phase-field effective stress for plasticity, and the dilative/compactive split and rate-dependent storage of plastic work. We construct a particular class of the framework by employing a Drucker–Prager plasticity model with a compression cap, and demonstrate that the proposed framework can capture brittle fracture, ductile flow, and their transition due to confining pressure and strain rate. [PDF] Our paper "A stabilized finite element formulation for monolithic thermo-hydro-mechanical simulations at finite strain" published in IJNME at 2015 is the top 5 most cited papers from 2015 to 2016. The paper can be downloaded via the Wiley Online Library [URL]. Computational thermo-hydro-mechanics for multiphase freezing and thawing porous media in the finite deformation range SeonHong Na, WaiChing Sun Abstract A stabilized thermo-hydro-mechanical (THM) finite element model is introduced to investigate the freeze-thaw action of frozen porous media in the finite deformation range. By applying mixture theory, frozen soil is idealized as a composite consisting of three phases, i.e., solid grain, unfrozen water and ice crystal. A generalized hardening rule at finite strain is adopted to replicate how the elasto-plastic responses and critical state evolve under the influence of phase transitions and heat transfer. The enhanced particle interlocking and ice strengthening during the freezing processes and the thawing-induced consolidation at the geometrical nonlinear regimes are both replicated in numerical examples. The numerical issues due to lack of two-fold inf-sup condition and ill-conditioning of the system of equations are addressed. Numerical examples for engineering applications at cold region are analyzed via the proposed model to predict the impacts of changing climate on infrastructure at cold regions. [DRAFT] A unified variational eigen-erosion framework for interacting brittle fractures and compaction bands in fluid-infiltrating porous media Kun, Wang WaiChing Sun Abstract The onset and propagation of the cracks and compaction bands, and the interactions between them in the host matrix, are important for numerous engineering applications, such as hydraulic fracture and CO2 storage. While crack may become flow conduit that leads to leakage, formation of compaction band often accompanies significant porosity reduction that prevents fluid to flow through. The objective of this paper is to present a new unified framework that predicts both the onset, propagation and interactions among cracks and compaction bands via an eigen-deformation approach. By extending the generalized Griffith's theory, we formulate a unified nonlocal scheme that is capable to predict the fluid-driven fracture and compression-driven anti-crack growth while incorporating the cubic law to replicate the induced anisotropic permeability changes triggered by crack and anti-crack growth. A set of numerical experiments are used to demonstrate the robustness and efficiency of the proposed model. [DRAFT] Our manuscript (co-authored by former student Zhijun Cai and postdoc scholar Dr. Jinhyun Choo) has been accepted by International Journal of Numerical Method in Engineering (see PDF). The abstract is listed below:
Mixed Arlequin method for multiscale poromechanics problems An Arlequin poromechanics model is introduced to simulate the hydro-mechanical coupling effects of fluid-infiltrated porous media across different spatial scales within a concurrent computational framework. A two-field poromechanics problem is first recast as the two-fold saddle point of an incremental energy functional. We then introduce Lagrange multipliers and compatibility energy functionals to enforce the weak compatibility of hydro-mechanical responses in the overlapped domain. To examine the numerical stability of this hydro-mechanical Arlequin model, we derive a necessary condition for stability, the two-fold inf--sup condition for multi-field problems, and establish a modified inf--sup test formulated in the product space of the solution field. We verify the implementation of the Arlequin poromechanics model through benchmark problems covering the entire range of drainage conditions. Through these numerical examples, we demonstrate the performance, robustness, and numerical stability of the Arlequin poromechanics model. A semi-implicit discrete-continuum coupling method for porous media based on the effective stress principle at finite strain
Kun Wang, WaiChing Sun A finite strain multiscale hydro-mechanical model is established via an extended Hill-Mandel condition for two-phase porous media. By assuming that the effective stress principle holds at unit cell scale, we established a micro-to-macro transition that links the micromechanical responses at grain scale to the macroscopic effective stress responses, while modeling the fluid phase only at the macroscopic continuum level. We propose a dual-scale semi-implicit scheme, which treats macroscopic responses implicitly and microscopic responses explicitly. The dual-scale model is shown to have good convergence rate, and is stable and robust. By inferring effective stress measure and poro-plasticity parameters, such as porosity, Biot’s coefficient and Biot’s modulus from RVE, the multiscale model is able to predict effective poro-elasto-plastic responses without introducing additional phenomenological laws. The performance of the proposed framework is demonstrated via a collection of representative numerical examples. Fabric tensors of the representative elementary volumes are computed and analyzed via the anisotropic critical state theory when strain localization occurs. New paper on wave propagation in thermo-sensitive fully saturated porous media accepted in IJNAMG.1/4/2016 Wave propagation and strain localization in a fully saturated softening porous medium under the non-isothermal conditions [PDF]
SeonHong Na, WaiChing Sun Abstract The thermo-hydro-mechanical (THM) coupling effects on the dynamic wave propagation and strain localization in a fully saturated softening porous medium are analyzed. The characteristic polynomial corresponding to the governing equations of the THM system is derived, and the stability analysis is conducted to determine the necessary conditions for stability for both non-isothermal and adiabatic cases. The result from the dispersion analysis based on the Abel-Ruffini theorem reveals that the roots of the characteristic polynomial for the thermo-hydro-mechanics problem can not be expressed algebraically. Meanwhile, the dispersion analysis on the adiabatic case leads to a new analytical expression of the internal length scale. Our limit analysis on the phase velocity for the non-isothermal case indicates that the internal length scale for the non-isothermal THM system may vanish at the short wavelength limit. This result leads to the conclusion that the rate-dependence introduced by multiphysical coupling may not regularize the THM governing equations when softening occurs. Numerical experiments are used to verify the results from the stability and dispersion analyses. 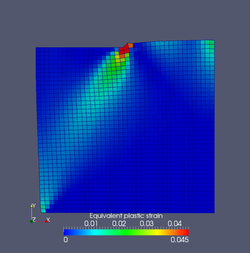 equivalent plastic strain triggered by punch loads equivalent plastic strain triggered by punch loads The manuscript titled "Modeling the hydro-mechanical responses of strip and circular punch loadings on water-saturated collapsible geomaterials" has been accepted by Acta Geotechnica today. Co-authors included Qiushi Chen from Clemson University and Jakob T Ostien from Sandia National Laboratories. The accepted paper can be found in Springerlink URL listed below. http://link.springer.com/article/10.1007/s11440-013-0276-x |
Group NewsNews about Computational Poromechanics lab at Columbia University. Categories
All
Archives
July 2023
|









 RSS Feed
RSS Feed